《Neural Networks and Deep Learning》一書的中文譯名是《神經網路與深度學習》，書如其名，不需要解釋也知道它是講什麼的，這是本入門級的好書。 在第一章中，作者展示瞭如何編寫一個簡單的、用於識別MNIST資料的Python神經網路程式。對於武林高手來說，看懂程式不會有任何困難，但對於我這樣的Python渣則有很多困惑。所以我對做了一些筆記，希望同時也可以幫助有需要的人。

『1』原文及程式 在這裡，先把中譯版部分貼上來，以方便後面的筆記記錄（這只是一部分）：

在給出一個完整的清單之前，讓我解釋一下神經網路程式碼的核心特徵，如下。核心是一個Network類，我們用來表示一個神經網路。這是我們用來初始化一個Network物件的程式碼:

class Network(object):

    def __init__(self, sizes):
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x) 
                        for x, y in zip(sizes[:-1], sizes[1:])]

在這段程式碼中，列表sizes包含各層的神經元的數量。因此舉個例子，如果我們想建立一個在第一層有2個神經元，第二層有3個神經元，最後一層有1個神經元的network物件，我們應這樣寫程式碼：

net = Network([2, 3, 1])

Network物件的偏差和權重都是被隨機初始化的，使用Numpy的np.random.randn函式來生成均值為0，標準差為1的高斯分佈。隨機初始化給了我們的隨機梯度下降演算法一個起點。在後面的章節中我們將會發現更好的初始化權重和偏差的方法，但是現在將採用隨機初始化。注意Network初始化程式碼假設第一層神經元是一個輸入層，並對這些神經元不設定任何偏差，因為偏差僅在之後的層中使用。

同樣注意，偏差和權重以列表儲存在Numpy矩陣中。因此例如net.weights[1]是一個儲存著連線第二層和第三層神經元權重的Numpy矩陣。（不是第一層和第二層，因為Python列中的索引從0開始）因此net.weights[1]相當冗長， 讓我們就這樣表示矩陣

w

。矩陣中的

wjk

是連線第二層的

kth

神經元和第三層的

jth

神經元的權重。

『2』程式解讀 正如上面的程式碼示例，建立一個Network物件的時候，傳入的是一個list，例如 [2, 3, 1]，list中有幾個元素就表示神經網路有幾層，從list中的第一個元素開始，每一個元素依次表示第1層、每2層、……第n層的神經元的數量。 這個不難理解，比較難理解的是 bias（偏差）以及 weight（權重）的表示方式。 文章來源：http://www.codelast.com/ 我們先來看 bias（偏差）：

self.biases = [np.random.randn(y, 1) for y in sizes[1:]]

首先需要明確的是，中括號表明了 biases 是一個list，中括號裡的內容是對這個list進行賦值的程式碼，它採用了一個for迴圈的方式來賦值，例如下面的程式碼：

a = [i for i in range(3)]
print(a)

會輸出結果：

[0, 1, 2]

所以，np.random.randn(y, 1) for y in sizes[1:] 這部分程式碼表達的就是—— list中的每一個元素都是 np.random.randn(y, 1) 這個表示式的計算結果，而這個表示式是含有變數 y 的，y 必須要有實際的值才能計算，所以用一個for迴圈來給 y 賦值，y 能取的所有值就是對 sizes[1:] 這個list進行遍歷得到的。前面已經說過了，sizes本身是一個list，而sizes[1:] 表示的是取這個 list 從第2個元素開始的子集，給個例子：

a = [5, 6, 8]
print(a[1:])

會輸出：

[6, 8]

所以，在我們前面用 net = Network([2, 3, 1]) 這樣的程式碼來建立了一個物件之後，sizes[1:] 的內容其實就是 [3, 1]，所以 y 的取值就是 3 和 1，所以 biases 這個list的第一個元素就是 np.random.randn(3, 1)，第二個元素就是 np.random.randn(1, 1)。 文章來源：http://www.codelast.com/ 我覺得經過這樣解釋，biases 在結構上看來是什麼東西已經比較清楚了吧？ 那麼話說回來，我們雖然知道了 np.random.randn(3, 1) 是 biases 的第一個元素，但 np.random.randn() 又是什麼鬼？ 且聽我道來： np 是這個Python程式 import 進來的Numpy庫的縮寫：

import numpy as np

randn() 是Numpy這個庫中，用於生成標準正態分佈資料的一個函式。其實 randn(3, 1) 生成的是一個3x1的隨機矩陣，我們可以在Python命令列中直接試驗一下：

import numpy as np

np.random.randn(3, 1)

輸出結果如下：

array([[ 1.33160979],

​ [ 0.66314905],

​ [ 0.27303603]])

可見，它輸出的是一個3行，1列的隨機數矩陣——你看這輸出多體貼，為了表明“3行1列”，它沒有把數字都排在一行，而是特意放在了3行裡。 好了，現在我們已經徹底瞭解了 biases 的結構，那麼再來看看，為什麼它的第一個元素是3x1的矩陣，第二個元素是1x1的矩陣呢？ 這跟要建立的神經網路層的結構有關。 文章來源：http://www.codelast.com/ 如作者書中所說，“假設第一層神經元是一個輸入層，並對這些神經元不設定任何偏差，因為偏差僅在之後的層中使用”，所以 biases 只有兩個元素，而不是3個。但知道了這一點並不能解決我們心中的疑惑：為什麼 biases[0] 是一個 3x1 的矩陣，biases[1] 是一個 1x1 的矩陣呢？

這就跟weight（權重）有關了，所以，我們不妨先來看看程式碼中，weight是如何定義的：

self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]

這個冗長的實現需要“細細品味”。 首先，中括號表明 weights 是一個list，中括號裡的程式碼對這個list的每一個元素進行賦值，list中的每一個元素都是一個 np.random.randn(y, x) ——這個東西我們剛才在解釋 biases 的時候已經說過了，它是一個y行x列的隨機數矩陣。那麼y和x的具體值又是什麼呢？它們是由for迴圈定義的：

for x, y in zip(sizes[:-1], sizes[1:])

首先要注意，這裡是按 x, y 的順序來賦值的，而不是 y, x，這和 np.random.randn(y, x) 中的順序相反。 其中，zip()是Python的一個內建函式，它接受一系列可迭代的物件（例如，在這裡是兩個list）作為引數，將物件中對應的元素打包成一個個tuple（元組），然後返回由這些tuples組成的list。 為了形象地說明zip()的作用，我們來看看這句簡單的程式碼：

zip([3, 4], [5, 9])

它的輸出是：

[(3, 5), (4, 9)]

可見，zip() 分別取出 [3, 4] 以及 [5, 9] 這兩個 list 的第一個、第二個元素，然後合成了兩個 tuple：(3, 5) 和 (4, 9)，然後再把這兩個tuple組成一個list：[(3, 5), (4, 9)]。所以，假設我們有如下程式碼：

for x, y in zip([3, 4], [5, 9])

那麼 x, y 的取值就有兩組了：3, 5 和 4, 9。 有了這樣直觀的對比，我們已經可以理解 for x, y in zip(sizes[:-1], sizes[1:]) 是什麼含義了。其實 sizes 就是一個含有3個元素的list：[2, 3, 1]，因此 sizes[:-1] 就是去掉最後一個元素的子list，即 [2, 3]；而 sizes[1:] 就是去掉第一個元素的子list，即 [3, 1]。 所以現在真相大白：x, y 的取值有兩組，一組是 2, 3，另一組是 3, 1。 再回去看 weights 的賦值程式碼，於是可以秒懂：weights 的第一個元素 weights[0] 是一個 3x2 的隨機數矩陣，weights 的第二個元素 weights[1] 是一個 1x3 的隨機數矩陣。 文章來源：http://www.codelast.com/ 現在總結一下： biases[0]：3x1 的矩陣 biases[1]：1x1 的矩陣 weights[0]：3x2 的矩陣 weights[1]：1x3 的矩陣

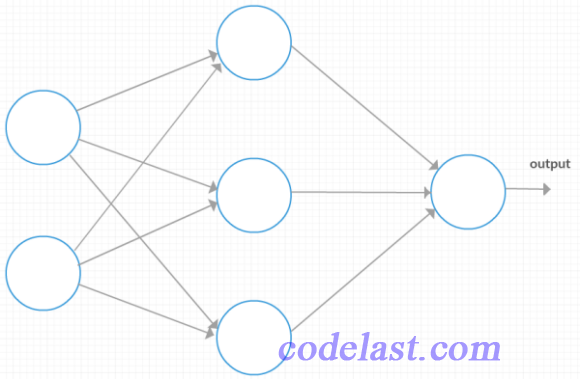
雖然我們已經精確分析出了那段程式碼的含義，但有人可能還是要問：為什麼建立的bias和weight是這些維度的？ 為了能幫助理解，我們畫出這個神經網路的結構（第一層有2個神經元，第二層有3個神經元，最後一層有1個神經元）： 文章來源：http://www.codelast.com/ 從圖上我們可以一眼看出，第一層的輸入向量（也就是 wx+b 中的 x ）是一個2行1列的向量，或者說是一個 2x1 的矩陣；第二層的 x 是一個3行1列的向量，或者說是一個 3x1 的矩陣。 我們知道，除了輸出層（output）之外，每一層的輸入 x 都要經過一個 wx+b 的運算（這裡忽略了激勵函式），得到一個矩陣，作為下一層的輸入。式中既然有weight（w）和 x 向量的點乘，weight矩陣的列數就必須和 x 向量的行數相等，所以這裡是不是恰好符合這個規則呢？ 來看看： 第一層→第二層的 wx+b 運算就是 weight[0]矩陣 ⋅x + biases[0] 矩陣，即 (3x2矩陣) ⋅ (2x1矩陣) + (3x1矩陣)，結果是一個 3x1 的矩陣，這個矩陣，作為下一層的輸入，實際上就是下一層的 x 。前面我們分析過，第二層的 x 應該是一個 3x1 的矩陣，這與運算結果完全相符。 第二層→第三層的 wx+b 運算就是 weight[1]矩陣 ⋅x + biases[1] 矩陣，即 (1x3矩陣) ⋅ (3x1矩陣) + (1x1矩陣)，結果是一個 1x1 的矩陣，其實就是一個標量，由於後面已經沒有其他層，所以這個標量就是整個神經網路的output。

通過以上不厭其煩的分析，相信任何人都能搞明白那僅有不到10行的程式碼是如何巧妙地定義了一個神經網路，搞定！