Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.

 Rules for a valid pattern:

1. Each pattern must connect at least m keys and at most n keys.
2. All the keys must be distinct.
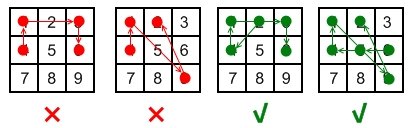
3. If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
4. The order of keys used matters.

思路：

1. 求路徑可行性，需要返回 —— 回溯

2. 用過的不能再用—— map

3. 下面是遍歷1-9的做法，其實對稱性可以看出1，3，7，9是一樣的數量，2，4，6，8是一樣數量，5單獨一個數量。這樣只用算三個數量即可。有時間實現。

 1 class Solution {
 2 public:
 3 int numberOfPatterns(int m, int n) {
 4     if (m > 9 || m < 1 || n > 9 || n < 1) return 0;
 5     vector<int> path;
 6     int ret = 0;
 7     set<int> used;
 8
 
     helper(m, n, path, used, ret);
 9     return ret;
10 }
11 void helper(int m, int n, vector<int> path, set<int> used, int& ret) {
12     if (used.size() >= m && used.size() <= n) ret++;
13     if (used.size() == n) return;
14     for (int i = 1; i <= 9; i++) {
15         if(used.count(i)) continue;
16         if (path.empty()) {
17             path.push_back(i);
18             used.insert(i);
19             helper(m, n, path, used, ret);
20             path.pop_back();
21             used.erase(i);
22         }
23         else {
24             bool cond1 = path.back() % 2 == 1 && i == 5;
25             bool cond2 = path.back() == 5;
26             bool cond3 = path.back() % 2 == 1 && i % 2 == 1 && path.back() != 5 && used.count((path.back() + i) / 2) != 0;
27             bool cond4 = path.back() % 2 == 1 && i % 2 == 0;
28             bool cond5 = path.back() % 2 == 0 && (path.back() + i) / 2 == 5 && used.count(5) != 0;
29             bool cond6 = path.back() % 2 == 0 && (path.back() + i) != 10;
30             if (cond1 || cond2 || cond3 || cond4 || cond5 || cond6) {
31                 path.push_back(i);
32                 used.insert(i);
33                 helper(m, n, path, used, ret);
34                 path.pop_back();
35                 used.erase(i);
36             }
37         }
38     }
39 }
40 };