揹包問題

寫這篇文章主要是為了幫幫新人吧,dalao勿噴.qwq

一般的揹包問題問法

　每種物品都有一個價值w和體積c.//這個就是下面的變數名,請看清再往下看.

　你現在有一個揹包容積為V,你想用一些物品裝揹包使得物品總價值最大.

01揹包

　　多種物品,每種物品只有一個.求能獲得的最大總價值.

　我們考慮是否選擇第i件物品時,是需要考慮前i-1件物品對答案的貢獻的.

分析

　如果我們不選擇第i件物品,那我們就相當於是用i-1件物品,填充了體積為v的揹包所得到的最優解.

　而我們選擇第i件物品的時候,我們要得到體積為v的揹包,我們需要通過填充用i-1件物品填充得到的體積為v-c[i]的揹包得到體積為v的揹包.

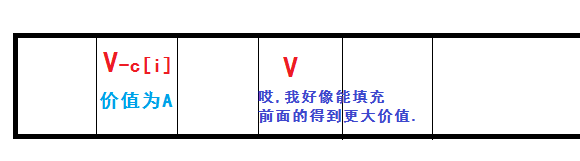
//請保證理解了上面加粗的字再往下看.

所以根據上面的分析,我們很容易設出01揹包的二維狀態

\(f[i][v]\)代表用i件物品填充為體積為v的揹包得到的最大價值.

從而很容易的寫出狀態轉移方程

\(f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i])\)

狀態轉移方程是如何得來的?

對於當前第\(i\)件物品,我們需要考慮其是否能讓我們得到更優解.

顯然,根據上面的話

我們選擇第i件物品的時候,我們要得到體積為v的揹包,我們需要通過填充用i-1件物品填充得到的體積為v-c[i]的揹包得到體積為v的揹包.

我們需要考慮到\(v-c[i]\)的情況.

當不選當前第\(i\)

件物品的時候,就對應了狀態轉移方程中的\(f[i-1][v]\),

而選擇的時候就對應了\(f[i-1][v-c[i]]+w[i]\).

Q:是不是在狀態轉移方程中一定會選擇當前i物品?

A:不會

我們考慮一個問題.

如果一個體積為5的物品價值為10,而還有一個體積為3的物品價值為12,一個體積為2的物品價值為8.顯然我們會選擇後者.

這樣我們的狀態轉移方程中就不一定會選擇i物品。

其實最好地去理解揹包問題的話,還是手跑一下這個過程,會加深理解。

程式碼寫法↓

for(int i=1;i<=n;i++)//列舉 物品 
    for(int j=1;j<=V;j++)//列舉體積 
        if(j>=c[i]）
            f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i]);//狀態轉移方程.
        else f[i][j]=f[i-1][j].
        
        //上面的if語句是判斷當前容量的揹包能否被較小體積的揹包填充得到.
        //顯然 如果j-c[i]<0我們無法填充
        //(誰家揹包負的體積啊 (#`O′)
 

但是二維下的01揹包們還是無法滿足,怎麼辦?

考慮一維如何寫!

仔細觀察會發現,二維狀態中,我們的狀態每次都會傳遞給i(就是說我們的前幾行會變得沒用.)

這就給了我們寫一維dp的機會啊

所以我們理所當然地設狀態\(f[i]\)代表體積為i的時候所能得到的最大價值.

容易發現的是,我們的\(f[i]\)只會被i以前的狀態影響.

如果我們順序列舉,我們的\(f[i]\)可能被前面的狀態影響.

所以我們考慮倒敘列舉,這樣我們的\(f[i]\)不會被i以前的狀態影響,而我們更新的話也不會影響其他位置的狀態.

(可以手繪一下這個過程,應該不是很難理解.)

或者來這裡看看(可能圖畫的有點醜了

程式碼寫法↓

for(int i=1;i<=n;i++)//列舉 物品 
    for(int j=V;j>=c[i];j--)//列舉體積 
        f[j]=max(f[j],f[j-c[i]]+w[i]);//狀態轉移方程. 

//應該不是很難理解.

小結

01揹包問題是揹包問題中最基礎,也是最典型的問題.其狀態轉移方程也是基礎,更可以演變成其他揹包的問題.

請保證看懂之後再向下看.

完全揹包

　 此類揹包問題中,我們的每種物品有無限多個,可重複選取.

　類似於01揹包,我們依舊需要考慮前i-1件物品的影響.

此時我們依舊可以設得二維狀態

\(f[i][v]\)代表用i件物品填充為體積為v的揹包得到的最大價值

依舊很容易寫出狀態轉移方程

\(f[i][v]=max(f[i-1][v],f[i-1][j-k*c[i]]+k*w[i])\)

//其中k是我們需要列舉的物品件數.而我們最多選取\(\left\lfloor\frac{V}{c[i]}\right\rfloor\)個(這個應該不用解釋

code

for(int i=1;i<=n;i++)//列舉物品
        for(int k=1;k<=V/c[i];k++)//我們的物品最多隻能放件.
            for(int j=1;j<=t;j++)
            {
                if(c[i]*k<=j)
                    f[i][j]=max(f[i-1][j],f[i-1][j-k*c[i]]+k*w[i]);
                else 
                    f[i][j]=f[i-1][j];
                 //判斷條件與01揹包相同.
            }
        

同樣地,我們去考慮一維狀態(鬼才會考慮

依舊設

\(f[i]\)代表體積為i的時候所能得到的最大價值

與01揹包不同的是,我們可以重複選取同一件物品.

此時,我們就需要考慮到前面i-1件物品中是否有已經選取過(其實沒必要

即,我們當前選取的物品,可能之前已經選取過.我們需要考慮之前物品對答案的貢獻.

因此我們需要順序列舉.

與01揹包一維的寫法類似.

程式碼寫法↓

code

for(int i=1;i<=n;i++)//列舉物品
    for(int j=c[i];j<=V;j++)//列舉體積.注意這裡是順序/
        f[j]=max(f[j,f[j-c[i]]]+w[i]);//狀態轉移.

如果還是不理解,來這裡看看.(就是上面那個連線)

小結

完全揹包也是類似於01揹包,應該也算上是它的一種變形.

比較一般的寫法是一維寫法,希望大家能掌握.

多重揹包

此類問題與前兩種揹包問題不同的是,

這裡的物品是有個數限制的.

(下面用\(num[i]\)表示物品i的個數.

我們可以列舉物品個數,也可以二進位制拆分打包

同樣,我們最多可以放\(\left\lfloor\frac{V}{c[i]}\right\rfloor\),但我們的物品數量可能不夠這麼多.

因此,我們列舉的物品個數是\(min(\left\lfloor\frac{V}{c[i]}\right\rfloor,num[i])\)

(其實沒這麼麻煩的,直接列舉到\(num[i]\)即可)

多個物品,我們就可以看成為一個大的物品,再去跑01揹包即可.

因此這個大物品的價值為\(k\)×\(w[i]\),體積為\(k\)×\(c[i]\)

code

for(int i=1;i<=n;i++)//列舉物品
    for(int j=V;j>=0;j--)//列舉體積
        for(int k=1;k<=num[i],k++)
            //這個列舉到num[i]更省心
            if(j-k*c[i]>=0)//判斷能否裝下.
                f[j]=max(f[j],f[j-k*c[i]]+k*w[i]);

其實還可以對每種物品的個物品跑01揹包問題,效率特別低

這裡也給出程式碼

code

for(int i=1;i<=n;i++)
    for(int k=1;k<=num[i];k++)
        for(int j=V;j>=c[i];j--)
            f[j]=max(f[j],f[j-c[i]]+w[i]);

但是此類問題,我們的一般解法卻是

二進位制拆分

二進位制拆分的原理

我們可以用 \(1,2,4,8...2^n\) 表示出\(1\) 到 \(2^{n+1}-1\)的所有數.

考慮我們的二進位制表示一個數。

根據等比數列求和,我們很容易知道我們得到的數最大就是\(2^{n+1}-1\)

而我們某一個數用二進位制來表示的話,每一位上代表的數都是\(2\)的次冪.

就連奇數也可以,例如->\(19\)可以表示為\(10010_{(2)}\)

這個原理的話應該很好理解,如果實在理解不了的話,還是動手試一試,說服自己相信這一原理.

二進位制拆分的做法

因為我們的二進位制表示法可以表示從\(1\)到\(num[i]\)的所有數,我們對其進行拆分,就得到好多個大物品(這裡的大物品代表多個這樣的物品打包得到的一個大物品).

(簡單來講,我們可以用一個大物品代表\(1,2,4,8..\)件物品的和。)

而這些大物品又可以根據上面的原理表示出其他不是2的次冪的物品的和.

因此這樣的做法是可行的.

我們又得到了多個大物品,所以再去跑01揹包即可.

這裡只給出拆分部分的程式碼,相信你可以碼出01揹包的程式碼.

code

for(int i=1;i<=n;i++)
{
    for(int j=1;j<=num[i];j<<=1)
    //二進位制每一位列舉.
    //注意要從小到大拆分
    {
        num[i]-=j;//減去拆分出來的
        new_c[++tot]=j*c[i];//合成一個大的物品的體積
        new_w[tot]=j*w[i];//合成一個大的物品的價值
    }
    if(num[i])//判斷是否會有餘下的部分.
    //就好像我們某一件物品為13,顯然拆成二進位制為1,2,4.
    //我們餘出來的部分為6,所以需要再來一份.
    {
        new_c[++tot]=num[i]*c[i];
        new_w[tot]=num[i]*w[i];
        num[i]=0;
    }
}

時間複雜度分析

我們拆分一種物品的時間複雜度為\(log(num[i])\).

我們總共會有n種物品,再配上列舉體積的時間複雜度.

因此,二進位制拆分做法的時間複雜度為\(O(\sum_{i=1}^nlog(num[i])\)×\(V )\)

單調佇列優化

首先回想多重揹包最普通的狀態轉移方程

\(f[i][j]=max(f[i-1][j],f[i-1][j-k*c[i]]+k*w[i])\)　

其中\(k \in [1,min(\left\lfloor\frac{V}{c[i]}\right\rfloor,num[i])]\)

下面用 \(lim\)表示\(min(\left\lfloor\frac{V}{c[i]}\right\rfloor,num[i])\)

容易發現的是\(f[i][j-k*c[i]]\)會被\(f[i][j-(k+1)*c[i]]\)影響 (很明顯吧

(我們通過一件體積為\(c[i]\)的物品填充體積為\(j-(k+1)*c[i]\)的揹包,會得到體積為\(j-k*c[i]\)的揹包.)

歸納來看的話

\(f[i][j]\)將會影響 \(f[i][j+k*c[i]]\)　\((j+k*c[i]<=V)\)

栗子

\(c[i]=4\)

容易發現的是,同一顏色的格子,對\(c[i]\)取模得到的餘數相同.

且,它們的差滿足等差數列! (公差為\(c[i]\).

通項公式為 \(j=k*c[i]+\)取模得到的餘數

所以我們可以根據對\(c[i]\)取模得到的餘數進行分組.

即可分為\(0,1,2,3{\dots}c[i]-1\) 共\(c[i]\)組

且每組之間的狀態轉移不互相影響.(注意這裡是組.相同顏色為一組

相同顏色的格子,位置靠後的格子,將受到位置靠前格子的影響.

//但是這樣的話,我們的格子會重複受到影響.(這裡不打算深入討論 害怕誤人子弟

即\(f[9]\)可能受到\(f[5]\)的影響,也可能受到\(f[1]\)的影響

而\(f[5]\)也可能受到\(f[1]\)的影響.

所以我們考慮將原始狀態轉移方程變形.

重點

這裡一些推導過程我會寫的儘量詳細(我也知道看不懂有多難受. qwq

令d=c[i],a=j/c[i],b=j%c[i]

其中a為全選狀況下的物品個數.

則\(j=a*d+b\)

則帶入原始的狀態轉移方程中

\(j-k*d = a*d+b-k*d\) $= (a-k)*d+b $

我們令\((a-k)=k^{'}\)

再回想我們最原始的狀態轉移方程中第二狀態 : \(f[i][j-k*c[i]]+k*w[i]\) 代表選擇\(k\)個當前\(i\)物品.

根據單步容斥 ：全選\(-\)不選=選.

因此 \(a-(a-k)=k\)

而前面我們已經令\((a-k)=k^{'}\)

而我們要求的狀態也就變成了

\(f[i][j]=max(f[i-1][k^{'}*d+b]+a*w[i]-k^{'}*w[i])\)

而其中,我們的\(a*w[i]\)為一個常量(因為a已知.)

所以我們的要求的狀態就變成了

\(f[i][j]=max(f[i-1][k^{'}*d+b]-k^{'}*w[i])+a*w[i]\)

根據我們的

\(k \in [1,lim]\)

容易推知

\(k^{'} \in [a-k,a]\)

那麼

當前的\(f[i][j]\)求解的就是為\(lim+1\)個數對應的\(f[i-1][k^{'}*d+b]-k^{'}*w[i]\)的最大值.

(之所以為\(lim+1\)個數,是包括當前這個\(j\),還有前面的物品數量.)

將\(f[i][j]\)前面所有的\(f[i-1][k^{'}*d+b]-k^{'}*w[i]\)放入一個佇列.

那我們的問題就是求這個最長為\(lim+1\)的佇列的最大值+\(a*w[i]\).

因此我們考慮到了單調佇列優化( ? ?ω?? )?

(這裡不再對單調佇列多說.這個題的題解中,有不少講解此類演算法的,如果不會的話還是去看看再來看程式碼.-->p1886 滑動視窗

//相信你只要仔細看了上面的推導過程,理解下面的程式碼應該不是很難.

//可能不久的將來我會放一個加註釋的程式碼(不是立flag.

//裡面兩個while應該是單調佇列的一般套路.

//這裡列舉的\(k\)就是\(k^{'}\).

code

for(int i=1;i<=n;i++)//列舉物品種類 
{
    cin>>c[i]>>w[i]>>num[i];//c,w,num分別對應 體積,價值,個數 
    if(V/c[i] <num[i]) num[i]=V/c[i];//求lim
    for(int mo=0;mo<c[i];mo++)//列舉餘數 
    {
        head=tail=0;//佇列初始化 
        for(int k=0;k<=(V-mo)/c[i];k++) 
        {
            int x=k;
            int y=f[k*c[i]+mo]-k*w[i];
            while(head<tail && que[head].pos<k-num)head++;//限制長度
            while(head<tail && que[tail-1].value<=y)tail--;
            que[tail].value=y,que[tail].pos=x;
            tail++;
            f[k*c[i]+mo]=que[head].value+k*w[i];
            //加上k*w[i]的原因:
            //我們的單調佇列維護的是前i-1種的狀態最大值.
            //因此這裡加上k*w[i].
        }
    }
}

時間複雜度分析

這裡只簡單的進行一下分析.(其實我也不大會分析 qwq

我們做一次單調佇列的時間複雜度為\(O(n)\)

而對應的每次列舉體積為\(O(V)\)

因此總的時間複雜度為\(O(n*V)\)

小結

多重揹包的寫法一般為二進位制拆分.

單調佇列寫法有些超出noip範圍,但時間複雜度更優,能掌握還是儘量去掌握.

拆分物品這種思想應該不算很難理解,這個是比較一般的寫法.希望大家能掌握.

如果還是比較抽象,希望大家能動筆嘗試一下.

例題-->p1776 寶物篩選(這個題之前還是個pj/tg-,後來竟然藍了 emmm

混合三種揹包

所謂的混合三種揹包就是存在三種物品。

一種物品有無數個(完全揹包),一種物品有1個(01揹包),一種物品有\(num[i]\)個(多重揹包)

這個時候一般只需要判斷是哪一種揹包即可,再對應地去選擇dp方程求解即可.

送上一波偽程式碼

code

for(int i=1;i<=n;i++)
{
    if(完全揹包) 
    {
        for(int j=c[i];j<=V;j++)
            f[j]=max(f[j],f[j-c[i]]+w[i]);
    }
    else if(01揹包) 
    {
        for(int j=V;j>=c[i];j--)
            f[j]=max(f[j],f[j-c[i]]+w[i]); 
    }
    else//否則就是完全揹包了 
    {
        for(int j=V;j>=0;j--)
            for(int k=1;k<=num[i];k++)
                if(j-k*c[i]>=0)
                    f[j]=max(f[j],f[j-k*c[i]]+k*w[i]);
    }
}

//完全揹包拆分的話,可以當做01揹包來做.(提供思路

小結

混合三種揹包問題應該不是很難理解(如果前面三種揹包你真正瞭解了的話.

結合起來考的話應該也不會很多.

(畢竟揹包問題太水了

例題:(這個我真的沒找到qwq

分組揹包

一般分組揹包問題中,每組中只能選擇一件物品.

狀態大家都會設\(f[k][v]\)代表前k組物品構成體積為v的揹包所能取得的最大價值和.

狀態轉移方程也很容易想.

\(f[k][v]=max(f[k-1][v],f[k-1][v-c[i]]+w[i])\)

但是我們每組物品中只能選擇一件物品.

//這個時候我們就需要用到01揹包倒敘列舉的思想.

code:

for(int i=1;i<=k;i++)//列舉組別
    for(int j=V;j>=0;j--)//列舉體積
        for(now=belong[i])//列舉第i組的物品.
        {
            if(j-c[i]>=0)
                f[i][j]=max(f[i-1][j],f[i-1][j-c[now]]+w[now]);
            else 
                f[i][j]=f[i-1][j];
        }

小結

這類問題是01揹包的演變,需要注意的位置就是我們列舉體積要在列舉第i組的物品之前

(因為每組只能選一個!)

有依賴的揹包

此類揹包問題中。如果我們想選擇物品i的附件,那我們必須選擇物品i.

就好比你買電扇必須先買電.

一個主件和它的附件集合實際上對應於分組揹包中的一個物品組.

每個選擇了主件又選擇了若干附件的策略,對應這個物品組的中的一個物品.

(也就是說,我們把'一個主件和它的附件集合'看成為了一個能獲得的最大價值的物品.)

具體實現呢?

我們的主件有一些附件伴隨,我們可以選擇購買附件,也可以不購買附件.

(當然我們也可以選擇不購買主件.

當我們選擇一個主件的時候,我們希望得到的肯定是最大價值.

如何做？

我們可以先對附件集合跑一遍01揹包,從而獲得這一主件及其附件集合的最大的價值.

(或者是完全揹包,視情況而定.)

程式碼大致寫法是這樣的↓

(每個物品體積為1,\(w[]\)代表價值.）

不敢保證正確性,不過一般都是這樣寫的qwq

for(int i=1;i<=n;i++)//列舉主件.
{
    memset(g,0,sizeof g);//做01揹包要初始化.
    for(now=belong[i])//列舉第i件物品的附件. 
    {
        for(int j=V-1;j>=c[now];j--)//因為要先選擇主件才能選擇附件,所以我們從V-1開始. 
        {
            g[j]=max(g[j],g[j-1]+w[now]);
        }
    }
    g[V]=g[V-1]+w[i];
    for(int j=V;j>=0;j--)
        for(int k=1;k<=V;k++)//此時相當於"打包" .. 
        {
            if(j-k>=0)
                f[j]=max(f[j],f[j-k]+w[i]+g[k-1]);
        }
}
printf("%d",f[V]); 

有一種情況,是主件的附件依舊有附件.(不會互相依賴.

對於這種依賴關係,我們可以構出這樣的圖.

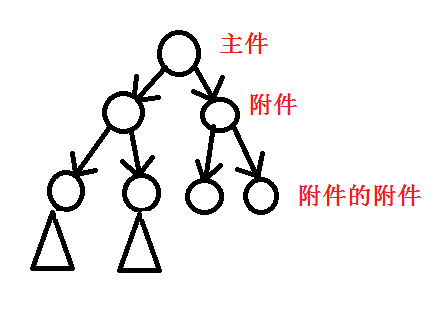
這種揹包就是傳說中的樹形揹包.

(樹形dp的一種)(應該後面會有人講)或者等我講

小結

這類問題更是揹包問題的延伸,我們需要考慮的就是如何取到每一個主件及其附件的集合中的最大值.而這就運用到了前面01揹包.

泛化物品

前面兩種揹包問題,已經有了泛化物品的影子.

(哪裡有啊!喂,話說這是什麼鬼東西

先給出概念.

該類物品並沒有固定的體積和價值，而是它的價值隨著你分配給它的體積而變化

其實這個可以抽象成一個函式圖象.

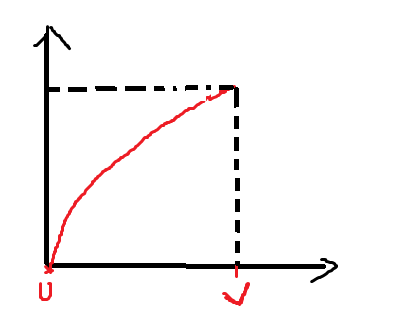
在定義域0~V中,此類物品的價值隨著分配給它的價值變化而變化.

(可能不是一次函式也不是二次函式.

畢竟我沒有遇到過這種題

現在應該很容易理解.

有依賴的揹包問題就有著這種泛化物品的思想.

如果對於某一個物品組,我們分配給它的體積越大,顯然它的價值越大.

最終我們的答案就是所有對答案有貢獻的物品組的和.(保證在限制範圍內.

這些物品組被分配體積的大小的限制就是0~V.

總的限制也是0~V,所以這就可以抽象為

最終結果\(f(V)=max(h(l)+g(V-l))\)

(這只是一個抽象的解釋,還需要具體問題具體分析.

揹包問題的變化.

隨著水平的提高(反正窩很弱QAQ

出題人會更加考察選手的思維.(話說有這種毒瘤出題人嘛qwq

下面討論幾種變化.根據揹包九講的順序.

輸出方案

對於一個揹包問題,我們已經得到了最大價值.

現在良心毒瘤出題人要求你輸出選擇物品的方案

分析

我們現在需要考慮的是如何記錄這個狀態.

很明顯記錄每個狀態的最優值,是由狀態轉移方程的哪一項推出來的.

如果我們知道了當前狀態是由哪一個狀態推出來的,那我們很容易的就能輸出方案.

開陣列\(g[i][v]\)記錄狀態\(f[i][v]\)是由狀態轉移方程哪一項推出.

//以01揹包一維寫法為例.

code

for(int i=1;i<=n;i++)
{
    for(int j=V;j>=c[i];j--)
    {
        if(f[j]<f[j-c[i]]+w[i])
        {
            f[j]=f[j-c[i]]+w[i];
                g[i][j]=true;///選第i件物品
        }
        else g[i][j]=false;///不選第i件物品
    }
}

輸出

code

int T=V;
for(int i=n;i>=1;i--)
{
    if(g[i][T])
    {
        printf("used %d",i);
        T-=c[i];//減去物品i的體積. 
    }
}

不敢保證正確性,不過一般都是這樣寫的qwq

再放一下狀態轉移方程.

\(f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i]\)

\(f[j]=max(f[j],f[j-c[i]]+w[i])\)

二維狀態可以省去g陣列,只需要判斷\(f[i][v]\)是等於\(f[i-1][v]\)還是等於\(f[i-1][v-c[i]]+w[i]\)就能輸出方案.

一維狀態好像不能,我不會啊qwq

輸出字典序較小的最優方案

感覺sort一下就可以吧

根據原文敘述來看,是將物品逆序排列一下.

與上面輸出方案的解法相同(倒敘列舉.

唯一需要判斷的是:

當\(f[i][v]==f[i-1][v]\) 並且\(f[i][v]==f[i-1][v-c[i]]+w[i]\)的時候.

我們要選擇後面這個方案.因為這樣選擇的話,我們會得到更小的字典序.(很明顯吧

** 求次優解or第k優解 **

此類問題應該是比較難理解.

所以我會盡量去詳細地解釋,qwq.

前置知識

首先根據01揹包的遞推式：(這裡按照一維陣列來講)

(v[i]代表物品i的體積,w[i]代表物品i的價值).

\(f(j)\)=\(max\left(f(j),f(j-v[i])+w[i]\right)\)

很容易發現\(f(j)\)的大小隻會與\(f(j)\)、\(f(j-v[i])+w[i]\)有關

我們設\(f[i][k]\)代表體積為i的時候,第k優解的值.

則從\(f[i][1]\)...\(f[i][k]\)一定是一個單調的序列.

\(f[i][1]\)即代表體積為i的時候的最優解

解析

很容易發現,我們需要知道的是,能否通過使用某一物品填充其他體積的揹包得到當前體積下的更優解.

我們用體積為7價值為10的物品填充成體積為7的揹包,得到的價值為10.
而我們發現又可以通過一件體積為3價值為12的物品填充一個體積為4價值為6的揹包得到價值為18.
此時我們體積為7的揹包能取得的最優解為18,次優解為10.
我們發現,這個體積為4的揹包還有次優解4(它可能被兩個體積為2的物品填充.)
此時我們可以通過這個次優解繼續更新體積為7的揹包.
最終結果為 18 16 10 

因此我們需要記錄一個變數c1表示體積為j的時候的第c1優解能否被更新.

再去記錄一個變數c2表示體積為j-v[i]的時候的第c2優解.

簡單概括一下

我們可以用v[i]去填充j-v[i]的揹包去得到體積為j的情況,並獲得價值w[i].
同理j-v[i]也可以被其他物品填充而獲得價值.
此時,如果我們使用的填充物不同,我們得到的價值就不同.

這是一個刷表的過程(或者叫推表?

為什麼是正確的?

(這裡引用一句話)

一個正確的狀態轉移方程的求解過程遍歷了所有可用的策略，也就覆蓋了問題的所有方案。

做法

考慮到我們的最優解可能變化,變化成次優解.只用一個二維陣列\(f[i][k]\)來實現可能會很困難.

所以我們引入了一個新陣列\(now[]\)來記錄當前狀態的第幾優解.

\(now[k]\)即代表當前體積為i的時候的第k優解.

因此最後我們可以直接將\(now[]\)的值賦給\(f[i]\)陣列

具體實現的話可以看看我的這篇文章

例題的話也就是這個(上面的文章是這題的題解.裡面有詳細解釋.

主要參考-->dd大牛的《揹包九講》

如果還是有不懂的地方,希望可以多多提問.

(畢竟我也不是個壞人,qwq)