Harris角點檢測演算法詳解
Harris角點演算法
特徵點檢測廣泛應用到目標匹配、目標跟蹤、三維重建等應用中,在進行目標建模時會對影象進行目標特徵的提取,常用的有顏色、角點、特徵點、輪廓、紋理等特徵。現在開始講解常用的特徵點檢測,其中Harris角點檢測是特徵點檢測的基礎,提出了應用鄰近畫素點灰度差值概念,從而進行判斷是否為角點、邊緣、平滑區域。Harris角點檢測原理是利用移動的視窗在影象中計算灰度變化值,其中關鍵流程包括轉化為灰度影象、計算差分影象、高斯平滑、計算區域性極值、確認角點。
一、基礎知識
影象的變化型別:
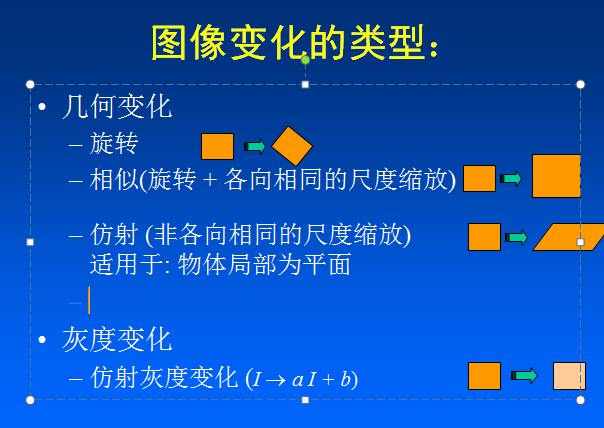
在特徵點檢測中經常提出尺度不變、旋轉不變、抗噪聲影響等,這些是判斷特徵點是否穩定的指標。
效能較好的角點:
- 檢測出影象中“真實”的角點
- 準確的定位效能
- 很高的重複檢測率
- 噪聲的魯棒性
- 較高的計算效率
角點的型別:

基於影象灰度的方法通過計算點的曲率及梯度來檢測角點,避免了第一類方法存在的缺陷,此類方法主要有Moravec運算元、Forstner運算元、Harris運算元、SUSAN運算元等。
二、Harris角點原理
1、演算法思想
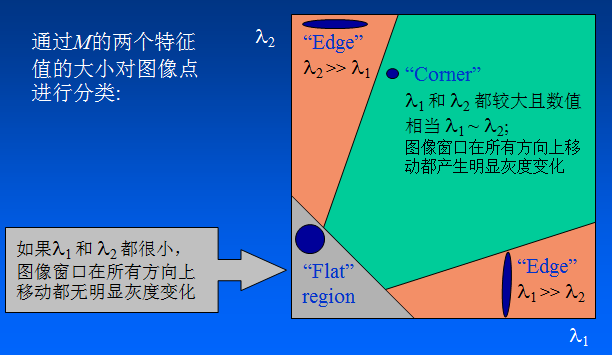
角點原理來源於人對角點的感性判斷,即影象在各個方向灰度有明顯變化。演算法的核心是利用區域性視窗在影象上進行移動判斷灰度發生較大的變化,所以此視窗用於計算影象的灰度變化為:[-1,0,1;-1,0,1;-1,0,1][-1,-1,-1;0,0,0;1,1,1]。人各個方向上移動這個特徵的小視窗,如圖3中視窗內區域的灰度發生了較大的變化,那麼就認為在視窗內遇到了角點。如圖1中,視窗內影象的灰度沒有發生變化,那麼視窗內就不存在角點;如果視窗在某一個方向移動時,視窗內影象的灰度發生了較大的變化,而在另一些方向上沒有發生變化,那麼,視窗內的影象可能就是一條直線的線段。
2、數學模型
根據演算法思想,構建數學模型,計算移動視窗的的灰度差值。
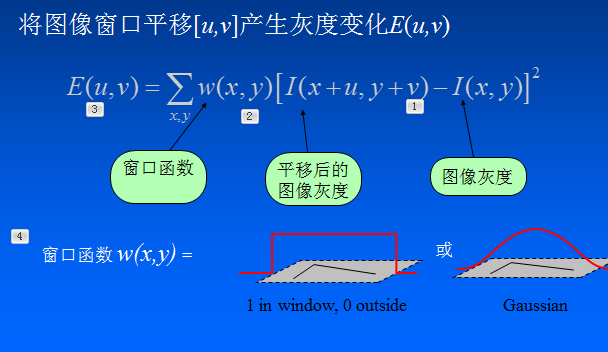
為了減小計算量,利用泰勒級數進行簡化公式:
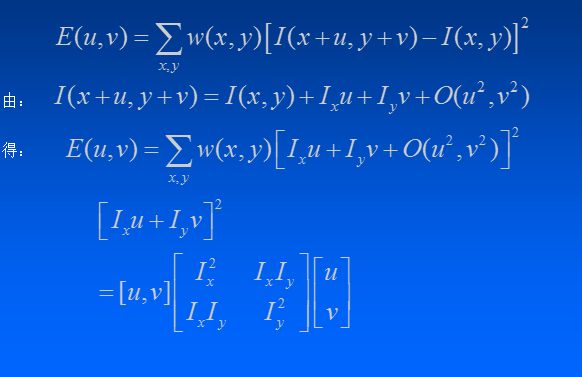

上圖中W函式表示視窗函式,M矩陣為偏導數矩陣。對於矩陣可以進行對稱矩陣的變化,假設利用兩個特徵值進行替代,其幾何含義類似下圖中的表達。在幾何
模型中通過判斷兩個特徵值的大小,來判定畫素的屬性。
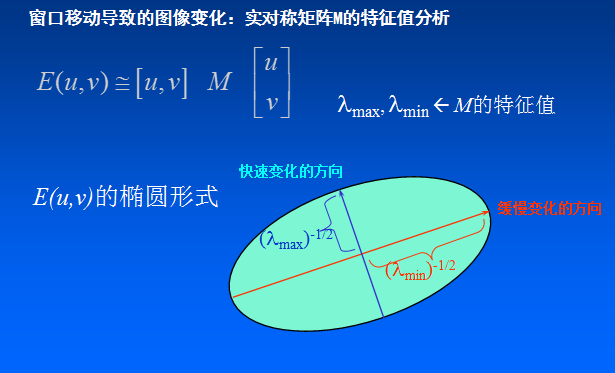
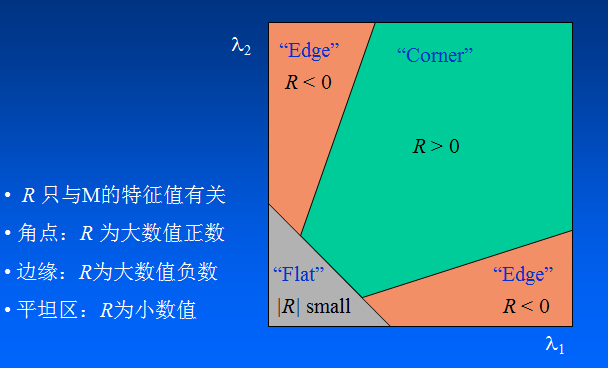
M為梯度的協方差矩陣 ,在實際應用中為了能夠應用更好的程式設計,定義了角點響應函式R,通過判定R大小來判斷畫素是否為角點。
R取決於M的特徵值,對於角點|R|很大,平坦的區域|R|很小,邊緣的R為負值。

3、演算法流程
1.利用水平,豎直差分運算元對影象的每個畫素進行濾波以求得Ix,Iy,進而求得M中的四個元素的值。
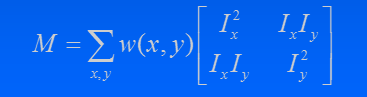
演算法原始碼:
程式碼中如果array為-1,0,1,-1,0,1,-1,0,1}則是求解X方向的,如果為{-1,-1,-1,0,0,0,1,1,1}為Y方向的,則Ix和Iy求解結束

//C程式碼
//這裡的size/2是為了不把影象邊界算進去。
//array也就是3*3的視窗函式為:double dx[9]={-1,0,1,-1,0,1,-1,0,1};或者 //定義垂直方向差分運算元並求Iy
double dy[9]={-1,-1,-1,0,0,0,1,1,1};
CvMat *mbys(CvMat *mat,int xwidth,int ywidth,double *array,int size1,int size2)//size
{
int i,j;
int i1,j1;
int px,py;
int m;
CvMat *mat1;
mat1=cvCloneMat(mat);
//為了去除邊界,從框體一半開始遍歷
for(i=size1/2;i<ywidth-size1/2;i++)
for(j=size2/2;j<xwidth-size2/2;j++)
{
m=0;
for(i1=0;i1<size1;i1++)
for(j1=0;j1<size2;j1++)
{
px=i-size1/2+i1;
py=j-size2/2+j1;
//CV_MAT_ELEM訪問矩陣元素
//每個元素和窗體函式遍歷相加
m+=CV_MAT_ELEM(*mat,double,px,py)*array[i1*size1+j1];
}
//賦值
CV_MAT_ELEM(*mat1,double,i,j)=m;
}
return mat1;
}

求解IX2相對比較簡單,畫素相乘即可。下面為基於opencv的C++版本,很是簡單

//構建模板 Mat xKernel = (Mat_<double>(1,3) << -1, 0, 1); Mat yKernel = xKernel.t(); //計算IX和IY Mat Ix,Iy; //可參考filter2d的定義 filter2D(gray, Ix, CV_64F, xKernel); filter2D(gray, Iy, CV_64F, yKernel); //計算其平方 Mat Ix2,Iy2,Ixy; Ix2 = Ix.mul(Ix); Iy2 = Iy.mul(Iy); Ixy = Ix.mul(Iy);

2.對M的四個元素進行高斯平滑濾波,為的是消除一些不必要的孤立點和凸起,得到新的矩陣M。

//本例中使用5×5的高斯模板
//計算模板引數
//int gausswidth=5;
//double sigma=0.8;
double *g=new double[gausswidth*gausswidth];
for(i=0;i<gausswidth;i++)//定義模板
for(j=0;j<gausswidth;j++)
g[i*gausswidth+j]=exp(-((i-int(gausswidth/2))*(i-int(gausswidth/2))+(j-int(gausswidth/2))*(j-int(gausswidth/2)))/(2*sigma));
//歸一化:使模板引數之和為1(其實此步可以省略)
double total=0;
for(i=0;i<gausswidth*gausswidth;i++)
total+=g[i];
for(i=0;i<gausswidth;i++)
for(j=0;j<gausswidth;j++)
g[i*gausswidth+j]/=total;
//進行高斯平滑
mat_Ix2=mbys(mat_Ix2,cxDIB,cyDIB,g,gausswidth,gausswidth);
mat_Iy2=mbys(mat_Iy2,cxDIB,cyDIB,g,gausswidth,gausswidth);
mat_Ixy=mbys(mat_Ixy,cxDIB,cyDIB,g,gausswidth,gausswidth);

利用opencv介面則是很簡單

//構建高斯函式 Mat gaussKernel = getGaussianKernel(7, 1); //卷積計算 filter2D(Ix2, Ix2, CV_64F, gaussKernel); filter2D(Iy2, Iy2, CV_64F, gaussKernel); filter2D(Ixy, Ixy, CV_64F, gaussKernel);

3.接下來利用M計算對應每個畫素的角點響應函式R,即:
也可以使用改進的R:
R=[Ix^2*Iy^2-(Ix*Iy)^2]/(Ix^2+Iy^2);裡面沒有隨意給定的引數k,取值應當比第一個令人滿意。

//計算cim:即cornerness of image,我們把它稱做‘角點量’
CvMat *mat_cim;
mat_cim=mbcim(mat_Ix2,mat_Iy2,mat_Ixy,cxDIB,cyDIB);
//用來求得響應度
CvMat *mbcim(CvMat *mat1,CvMat *mat2,CvMat *mat3,int xwidth,int ywidth)
{
int i,j;
CvMat *mat;
mat=cvCloneMat(mat1);
for(i = 0; i <ywidth; i++)
{
for(j = 0; j < xwidth; j++)
{
//注意:要在分母中加入一個極小量以防止除數為零溢位
CV_MAT_ELEM(*mat,double,i,j)=(CV_MAT_ELEM(*mat1,double,i,j)*CV_MAT_ELEM(*mat2,double,i,j)-
CV_MAT_ELEM(*mat3,double,i,j)*CV_MAT_ELEM(*mat3,double,i,j))/
(CV_MAT_ELEM(*mat1,double,i,j)+CV_MAT_ELEM(*mat2,double,i,j)+0.000001);
}
}
return mat;
}


//opencv程式碼
Mat cornerStrength(gray.size(), gray.type());
for (int i = 0; i < gray.rows; i++)
{
for (int j = 0; j < gray.cols; j++)
{
double det_m = Ix2.at<double>(i,j) * Iy2.at<double>(i,j) - Ixy.at<double>(i,j) * Ixy.at<double>(i,j);
double trace_m = Ix2.at<double>(i,j) + Iy2.at<double>(i,j);
cornerStrength.at<double>(i,j) = det_m - alpha * trace_m *trace_m;
}
}

4、區域性極大值抑制,同時選取其極大值

//--------------------------------------------------------------------------
// 第四步:進行區域性非極大值抑制
//--------------------------------------------------------------------------
CvMat *mat_locmax;
//const int size=7;
mat_locmax=mblocmax(mat_cim,cxDIB,cyDIB,size);
// cout<<CV_MAT_ELEM(*mat_locmax,double,cyDIB-1,cxDIB-1)<<endl;
//用來求得區域性極大值
CvMat *mblocmax(CvMat *mat1,int xwidth,int ywidth,int size)
{
int i,j;
double max=-1000;
int i1,j1;
int px,py;
CvMat *mat;
mat=cvCloneMat(mat1);
for(i=size/2;i<ywidth-size/2;i++)
for(j=size/2;j<xwidth-size/2;j++)
{
max=-10000;
for(i1=0;i1<size;i1++)
for(j1=0;j1<size;j1++)
{
px=i-size/2+i1;
py=j-size/2+j1;
if(CV_MAT_ELEM(*mat1,double,px,py)>max)
max=CV_MAT_ELEM(*mat1,double,px,py);
}
if(max>0)
CV_MAT_ELEM(*mat,double,i,j)=max;
else
CV_MAT_ELEM(*mat,double,i,j)=0;
}
return mat;
}

在opencv中應用maxminloc函式

// threshold double maxStrength; minMaxLoc(cornerStrength, NULL, &maxStrength, NULL, NULL); Mat dilated; Mat localMax; //預設3*3核膨脹,膨脹之後,除了區域性最大值點和原來相同,其它非區域性最大值點被 //3*3鄰域內的最大值點取代 dilate(cornerStrength, dilated, Mat()); //與原圖相比,只剩下和原圖值相同的點,這些點都是區域性最大值點,儲存到localMax compare(cornerStrength, dilated, localMax, CMP_EQ);

5.在矩陣R中,同時滿足R(i,j)大於一定閾值threshold和R(i,j)是某領域內的區域性極大值,則被認為是角點。

cv::Mat cornerMap; // 根據角點響應最大值計算閾值 threshold= qualityLevel*maxStrength; cv::threshold(cornerStrength,cornerTh, threshold,255,cv::THRESH_BINARY); // 轉為8-bit圖 cornerTh.convertTo(cornerMap,CV_8U);// 和區域性最大值圖與,剩下角點區域性最大值圖,即:完成非最大值抑制 cv::bitwise_and(cornerMap,localMax,cornerMap);
imgDst = cornerMap.clone();

for( int y = 0; y < cornerMap.rows; y++ )
{
const uchar* rowPtr = cornerMap.ptr<uchar>(y);
for( int x = 0; x < cornerMap.cols; x++ )
{
// 非零點就是角點
if (rowPtr[x])
{
points.push_back(cv::Point(x,y));
}
}
}


三、演算法原始碼
1、C版本
裡面函式最基礎的程式碼解釋和註釋
 C原始碼
C原始碼
2、基於opencv原始碼
 opencv+C++推薦
opencv+C++推薦
3、opencv中Harris介面
OpenCV的Hairrs角點檢測的函式為cornerHairrs(),但是它的輸出是一幅浮點值影象,浮點值越高,表明越可能是特徵角點,我們需要對影象進行閾值化。
C++: void cornerHarris(InputArray src, OutputArray dst, int blockSize, int apertureSize, double k, int borderType = BORDER_DEFAULT);
- src – 輸入的單通道8-bit或浮點影象。
- dst – 儲存著Harris角點響應的影象矩陣,大小與輸入影象大小相同,是一個浮點型矩陣。
- blockSize – 鄰域大小。
- apertureSize – 擴充套件的微分運算元大。
- k – 響應公式中的,引數$\alpha$。
- boderType – 邊界處理的型別。

int main()
{
Mat image = imread("../buliding.png");
Mat gray;
cvtColor(image, gray, CV_BGR2GRAY);
Mat cornerStrength;
cornerHarris(gray, cornerStrength, 3, 3, 0.01);
threshold(cornerStrength, cornerStrength, 0.001, 255, THRESH_BINARY);
return 0;
}

從上面上間一幅影象我們可以看到,有很多角點都是粘連在一起的,我們下面通過加入非極大值抑制來進一步去除一些粘在一起的角點。
非極大值抑制原理是,在一個視窗內,如果有多個角點則用值最大的那個角點,其他的角點都刪除,視窗大小這裡我們用3*3,程式中通過影象的膨脹運算來達到檢測極大值的目的,因為預設引數的膨脹運算就是用視窗內的最大值替代當前的灰度值。
 View Code
View Code
四、Harris角點性質
1、閾值決定檢測點數量
增大$\alpha$的值,將減小角點響應值$R$,降低角點檢測的靈性,減少被檢測角點的數量;減小$\alpha$值,將增大角點響應值$R$,增加角點檢測的靈敏性,增加被檢測角點的數量
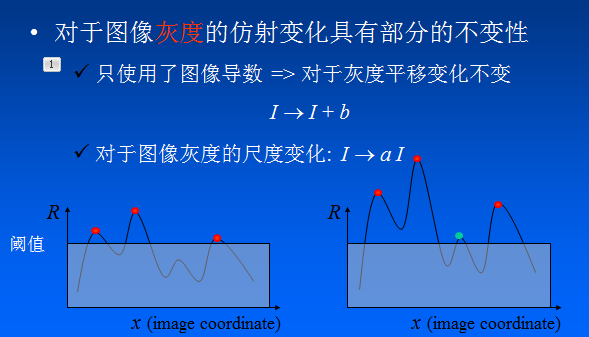
2、Harris角點檢測運算元對亮度和對比度的變化不敏感
這是因為在進行Harris角點檢測時,使用了微分運算元對影象進行微分運算,而微分運算對影象密度的拉昇或收縮和對亮度的擡高或下降不敏感。換言之,對亮度和對比度的仿射變換並不改變Harris響應的極值點出現的位置,但是,由於閾值的選擇,可能會影響角點檢測的數量。
3. Harris角點檢測運算元具有旋轉不變性
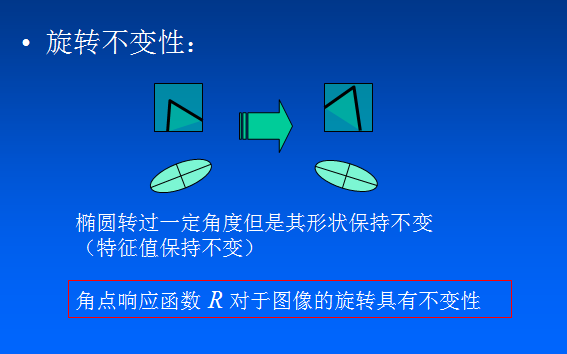
Harris角點檢測運算元使用的是角點附近的區域灰度二階矩矩陣。而二階矩矩陣可以表示成一個橢圓,橢圓的長短軸正是二階矩矩陣特徵值平方根的倒數。當特徵橢圓轉動時,特徵值並不發生變化,所以判斷角點響應值也不發生變化,由此說明Harris角點檢測運算元具有旋轉不變性。
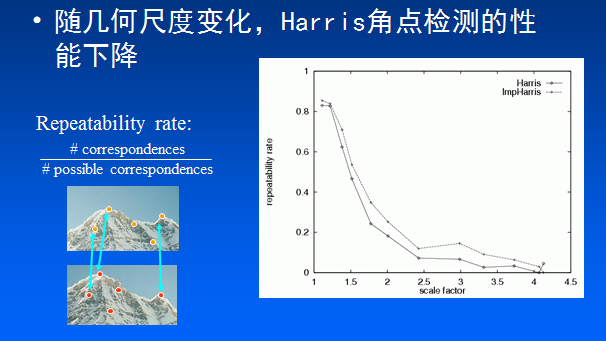
4. Harris角點檢測運算元不具有尺度不變性
如下圖所示,當右圖被縮小時,在檢測視窗尺寸不變的前提下,在視窗內所包含影象的內容是完全不同的。左側的影象可能被檢測為邊緣或曲線,而右側的影象則可能被檢測為一個角點。
五、函式備註
1、compare
功能:兩個陣列之間或者一個數組和一個常數之間的比較
結構:
void compare(InputArray src1, InputArray src2, OutputArray dst, int cmpop)
src1 :第一個陣列或者標量,如果是陣列,必須是單通道陣列。
src2 :第二個陣列或者標量,如果是陣列,必須是單通道陣列。
dst :輸出陣列,和輸入陣列有同樣的size和type=CV_8UC1
cmpop :
標誌指明瞭元素之間的對比關係
CMP_EQ src1 相等 src2.
CMP_GT src1 大於 src2.
CMP_GE src1 大於或等於 src2.
CMP_LT src1 小於 src2.
CMP_LE src1 小於或等於 src2.
CMP_NE src1 不等於 src2.
如果對比結果為true,那麼輸出陣列對應元素的值為255,否則為0

//獲取角點圖
Mat getCornerMap(double qualityLevel) {
Mat cornerMap;
// 根據角點響應最大值計算閾值
thresholdvalue= qualityLevel*maxStrength;
threshold(cornerStrength,cornerTh,
thresholdvalue,255,cv::THRESH_BINARY);
// 轉為8-bit圖
cornerTh.convertTo(cornerMap,CV_8U);
// 和區域性最大值圖與,剩下角點區域性最大值圖,即:完成非最大值抑制
bitwise_and(cornerMap,localMax,cornerMap);
return cornerMap;
}

2、bitwise_and(位運算函式)
功能:計算兩個陣列或陣列和常量之間與的關係
結構:
void bitwise_and(InputArray src1, InputArray src2, OutputArray dst, InputArray mask=noArray())
src1 :第一個輸入的陣列或常量
src2 :第二個輸入的陣列或常量
dst :輸出陣列,和輸入陣列有同樣的size和type
mask :可選擇的操作掩碼,為8位單通道陣列,指定了輸出陣列哪些元素可以被改變,哪些不可以
操作過程為:
如果為多通道陣列,每個通道單獨處理
3、filter2D
OpenCV中的內部函式filter2D可以直接用來做影象卷積操作
void filter2D(InputArray src, OutputArray dst, int ddepth, InputArray kernel, Point anchor=Point(-1,-1), double delta=0, int borderType=BORDER_DEFAULT )
六、參考文章
2、尺度空間理論
