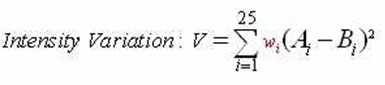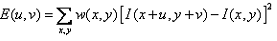Moravec角點檢測演算法
一、Moravec角點檢測演算法原理
Moravec角點檢測演算法的思想是: 在影象中設計一個區域性檢測視窗,當該視窗沿各個方向作微小移動時 ,
考查視窗的平均能量變化,當該能量變化值超過設定的閾值時,就將視窗的中心畫素點提取為角點。
此檢測視窗可以是3*3,也可以是5*5。現在就以3*3為例,至於平均能量用興趣值來表示。計算每個畫素
點的興趣值,就要在3*3的視窗中計算0度,45度,90度,135度四個方向灰度差的平方和,取其中最小值作為
該畫素點的興趣值,具體公式為:
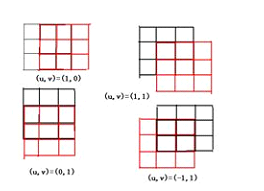
其中(u,v)是視窗移動的位移,(x,y)表示該視窗內的畫素點的座標,w(x,y)表示方形的二值視窗,若像
素點在視窗內,則取值為1,否則為0。四種移位(u,v)=(1,0),(1,1),(0,1),(-1,1),具體移位如圖:
二、角點檢測的步驟
1.對於每個畫素點,計算在E(u,v)的值,如果是3*3,(u,v)的值是(1,0),(1,1),(0,1),(-1,1)
如果是5*5的視窗,(u,v)的取值是(1,0),(1,1),(0,1),(-1,1),(-1,0),(-1,-1),
(0,-1),(1,-1)8種情況。
2.計算E(u,v)的最小值minValue
3,.對於每個位置minValue進行判斷,是不是大於設定的閾值,如果大於設定的閾值,就進行非區域性
極大值抑制,判斷是不是區域性極大值。
為什麼要進行非區域性極大值抑制?
因為在一個視窗內,中心點附近的值也可能大於閾值,但是要在這個視窗內排除這些值,確定區域性的最大
值,所以要進行非區域性極大值抑制。
三、具體程式碼如下
/**********************************************************************************
*函式 int getMoravec(IplImage* src,CvSeq* corners)
*輸入:
*src : 單通道影象
*corners : 用來儲存提取到的角點
*threshold : 角點量的閾值 (具體函式 請看視訊)
*輸出
*corners : 用來儲存提取到的角點
*返回值
*角點的個數
***************************************************************************************/
int getMoravec(IplImage* src,CvSeq* corners , float threshold)
{
//視窗大小
const int winSize=5;
int x,y,halfWinSize=winSize/2;
//儲存最小的變化量
IplImage* diffDst = cvCreateImage(cvGetSize(src),32,1);
cvZero(diffDst);
//儲存角點個數
int cornersCount=0;
//計算影象上每一個點上的 在4個方向上的變化量 並計算出最小值 儲存在矩陣diffDst中
for(y=halfWinSize;y<src->height-halfWinSize;y++)//把視窗的一半排除在迴圈以外,因為以第一個點為中心作為一個5*5的模板,該模板已經超出影象的範圍
{
for(x=halfWinSize;x<src->width-halfWinSize;x++)
{
//compute the reaction in the four directions(0,45,90,135)
int winx;
//陣列reaction[4] 用於保持 在四個方向上的灰度值變化量
//minValue用於儲存4個變化量中的最小值
float reaction[4],minValue;
reaction[0]=0;
reaction[1]=0;
reaction[2]=0;
reaction[3]=0;
//提示 下面的4個迴圈 可以綜合成一個迴圈
//0 度方向的變化量儲存在reaction[0]中
for( winx=-halfWinSize;winx<halfWinSize;winx++)//-2,-1,0,1
{
reaction[0] = reaction[0]+pow(cvGetReal2D(src,y,x+winx)-cvGetReal2D(src,y,x+winx+1),2);
}
//45 度方向的變化量儲存在reaction[1]中
for( winx=-halfWinSize;winx<halfWinSize;winx++)
{
reaction[1] = reaction[1]+pow(cvGetReal2D(src,y+winx,x+winx)-cvGetReal2D(src,y+winx+1,x+winx+1),2);
}
//0 度方向的變化量儲存在reaction[2]中
for( winx=-halfWinSize;winx<halfWinSize;winx++)
{
reaction[2] = reaction[2]+pow(cvGetReal2D(src,y+winx,x)-cvGetReal2D(src,y+winx+1,x),2);
}
//135 度方向的變化量儲存在reaction[3]中
for( winx=-halfWinSize;winx<halfWinSize;winx++)
{
reaction[3] = reaction[3]+pow(cvGetReal2D(src,y+winx,x-winx)-cvGetReal2D(src,y+winx+1,x-winx-1),2);
}
//計算4個量中最小值 儲存到minValue
minValue = reaction[0];
minValue = minValue > reaction[1] ? reaction[1] : minValue;
minValue = minValue > reaction[2] ? reaction[2] : minValue;
minValue = minValue > reaction[3] ? reaction[3] : minValue;
//將最小的變化量儲存到矩陣
cvSetReal2D(diffDst,y,x,minValue);
}
}
//獲取角點座標 判斷當前點的區域性極大值
for(y=halfWinSize;y<src->height-halfWinSize;)//這裡y和x不能每次都加1,因為在一個視窗內只能出現一個區域性最大值,也就是
{
for(x=halfWinSize;x<src->width-halfWinSize;)//要對視窗進行非極大值抑制
{
float max=0;
int flag = 0 ;
CvPoint maxLoc;
maxLoc.x = -1;
maxLoc.y = -1;
//首先計算以點(x,y)位中心的winSize*winSize的視窗內部的區域性極大值
for(int winy=-halfWinSize;winy<=halfWinSize;winy++)
{
for(int winx=-halfWinSize;winx<=halfWinSize;winx++)
{
float value ;
value = cvGetReal2D(diffDst,y+winy,x+winx);
//計算該視窗內 最大值 儲存到max 並儲存其座標到maxLoc
if(value>max)
{
max = value;
maxLoc.x = x+winx;
maxLoc.y = y+winy;
flag = 1;
}
}
}
//如果找到區域性極大值 並且該值大於預先設定的閾值 則認為是角點
if(flag==1 && max>threshold)
{
cvSeqPush(corners,&maxLoc);
cornersCount++;
}
//下一個視窗
x=x+halfWinSize;
}
//下一行的第一個視窗
y=y+halfWinSize;
}
cvReleaseImage(&diffDst);
return cornersCount;
}
四、moravec角點檢測缺點分析及檢測
moravec有兩個重要的缺點:
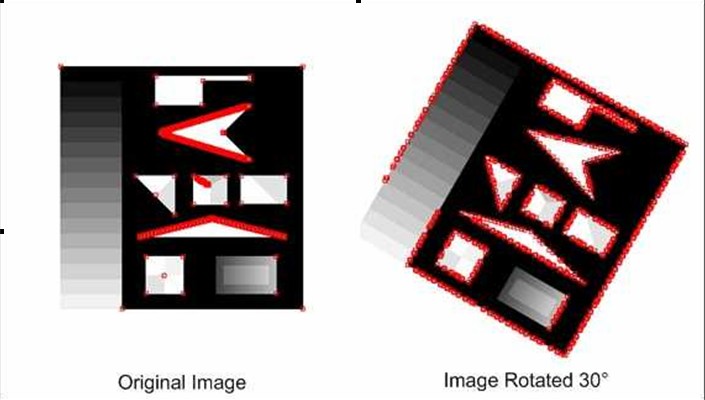
1.它不具備旋轉不變性
2.對邊緣點的反應比較強烈
moravec只計算了一些離散的偏移產生的灰度值變化(最多是8個方向),如圖下所示,旋轉之後,檢測到角點不一樣了。moravec統計的8個方向(最多是8個方向)是0°,45°,90°,135°,180°,225°,270°,315°。如果影象上的邊緣上的某個點,在旋轉前剛好是處於45°方向,此時檢測到不是角點(因為視窗在45°方向平移的時候,視窗內部畫素值變化肯定很小),當影象旋轉10°,此時該點處在55°,那麼現在就很有可能變成了一個角點(因為視窗只有在55°方向平移的時候,視窗內部的灰度值變化才會取到最小值,而55°不在moravec演算法的統計之內)。具體如圖:
下圖中,是用3*3的視窗,對影象進行morave角點檢測。雖然moravec演算法能把所有角點都檢測出來,但是把邊緣上面的很多點也作為角點了,對於這種情況,我們應該是可以理解的。moravec演算法對角點定義是:視窗在各個方向的移動,視窗內的灰度值都會產生較大的變化。而其實這裡的“各個方向“,最多也就只有8個方向。所以,如果邊緣的方向,是這8個方向以外的方向,那麼,就會被認為是角點。
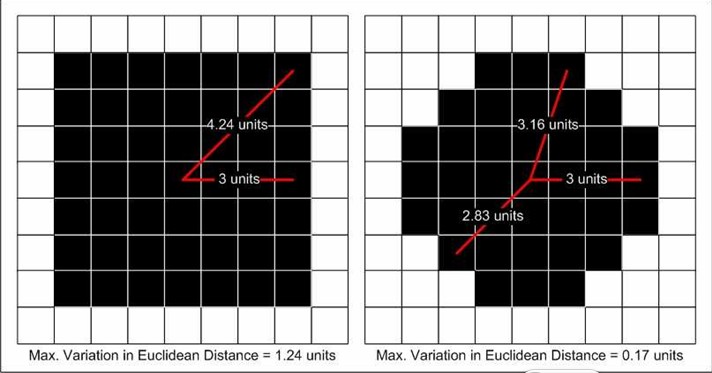
為了達到精確估計區域性灰度值的變化程度,圓形的窗口才是理想的。圓形的視窗,使得中心點到視窗的每一個邊緣點的歐式距離基本是相等的。如圖,左圖是7*7視窗,右圖是半徑為7的圓形視窗,可以看出,對於圓形視窗,從中心點到各個邊緣點之間的歐式距離更接近。這樣更有利於評估區域性灰度值的變化程度。為什麼呢?“評估區域性灰度值的變化程度“,注意這句話裡的一個關鍵詞”區域性“,那麼什麼是區域性?如果我們使用7*7的正方形視窗,那麼這個正方形視窗就是區域性,我們的評估區域性灰度值的變化程度的時候,這49個元素都會參與運算;當我們使用半徑為7的圓形視窗的時候,那麼這個半徑為7的圓形視窗就是區域性,在這個圓形視窗內的灰度值都會參與運算。
通常,我們認為,裡中心點更近的點,對該點影響也會大一些。既然離得比較近的點對中心點的影響比較大,那麼我們在評估區域性灰度值的變化程度的時候,應該賦予離中心更近的點更大的權重才是合理的,而不是moravec使用的視窗值,只要在視窗內部,不管遠近,權重都是1.
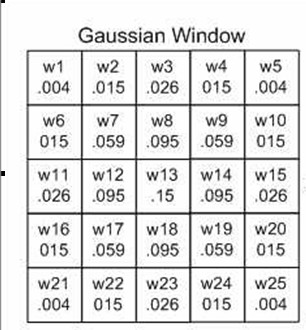
通過上面的分析,既要使用圓形的視窗,又要賦予離中心更近的點更大的權重,那麼高斯視窗就是比較好的一個選擇了。5*5的高斯視窗如圖所示:雖然看起來的也是方形的,但是它在四個角落上的權重是非常小的,可以近似的認為是0,那麼就可以認為是一個圓形的視窗,並且,權重是離中心點越近變得越大。