視訊網址：https://www.bilibili.com/video/av37567072/

程式碼網址：https://download.csdn.net/download/lykymy/10833542

實現思想

本次實驗主要是根據《Denoising point sets via L0 minimization》以及《Image Smoothing via L0 Graient Minimization》這兩篇論文實現的。在這兩篇論文中它們都涉及到同一個思想，那就是L0正規化的優化問題。其實際上就是藉助輔助變數，將L0優化問題轉化為L2優化問題，從而較為方便地進行求解。在這，我們可以發現，針對不同的處理物件，其設計的函式也不相同。下面將具體進行介紹。

關於L0以及其他的相關正規化的定義，可以參考我寫的相關部落格。

L0正規化實際上就是求解一個向量中非0向量的個數，其具體的表示式如下所示：

其中符號|*|0就是代表求解非0的個數。

我們的目的便是為了實現L0能量公式的最小化，即如下所示：

由於該公式很難直接求解出最優問題，因此需要引入輔助變數，將其轉化為基於L2的正規化進行最優解的求取。因此，上述公式可以轉化為下列公式：

下面就需要根據具體進行具體分析：

針對一維的訊號，S是表示輸入影象，D(S)是表示向量中非0的個數

針對二維的影象，S是表示影象中每個畫素的顏色，D(S)是表示顏色的梯度

針對三維的影象，S是表示網格中點的位置，D(S)是表示基於Laplcaian運算元的邊緣的導數

為了更好的求解上述公式，我們需要將其分解為兩個子問題：一個是求解S，另一個是求解輔助變數。

在求解輔助變數的時候，我們需要將S看成是一個常量，利用下述公式進行求解

通過歸納證明，可以得出

具體的證明過程可以參考這篇論文《Image Smoothing via L0 Graient Minimization》。

在求解S的時候，我們需要將輔助變數看成是一個常量，利用下述公式進行求解

我們將持續迭代上述公式，從而求解最優化問題。

通過上述的講解，我們發現：只要根據不同的情況，定義好不同的S以及D(S)便可以較為方便地將L0正規化轉化為L2正規化，從而快速地進行求解。

這裡我們定義：

S為影象的流場

D(S)為任意畫素與周圍上、下、左、右四個畫素的歐式距離

具體的實現演算法如下所示：

流場的繪製

正0度與正90度的影象

正25度與負25度的影象

正45度與負45度的影象

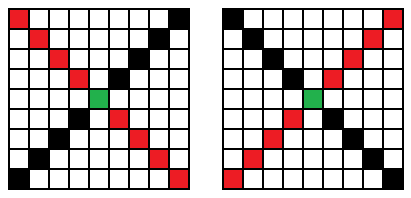
正75度與負75度的影象

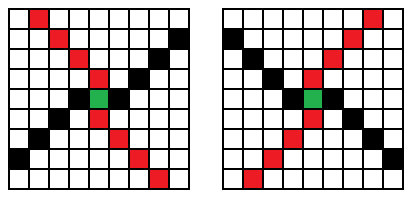
部分程式碼

//實現l0平滑影象
Mat l0_smooth(Mat & image, int nu, int mu, int beta_start, int beta_end)
{
    char energy_name[50] = "l0 smooth energy";
	//建立grad_x和grad_y矩陣
	Mat grad_x = Mat::zeros(image.size(), CV_16S);
	Mat grad_y = Mat::zeros(image.size(), CV_16S);
	//建立roberts運算元處理顯示圖片
	Mat roberts_img = Mat::zeros(image.size(), CV_16S);
	for (int i = 0; i < image.rows - 1; i++)
	{
		for (int j = 0; j < image.cols - 1; j++)
		{
			//求取roberts運算元水平方向的梯度
			grad_x.at<short>(i, j) = image.at<uchar>(i, j) - image.at<uchar>(i + 1, j + 1);
			//求取roberts運算元垂直方向的梯度
			grad_y.at<short>(i, j) = image.at<uchar>(i, j + 1) - image.at<uchar>(i + 1, j);
		}
	}
	//構建流場
	for (int i = 0; i < image.rows; i++)
	{
		for (int j = 0; j < image.cols; j++)
		{
			if (grad_x.at<short>(i, j) != 0)
			{
				roberts_img.at<short>(i, j) = atan(grad_y.at<short>(i, j) / grad_x.at<short>(i, j)) * 180 / 3.1415;
			}
			else
			{
				roberts_img.at<short>(i, j) = 90;
			}
		}
	}
	//Mat zeta_value = sobel_img.clone();
	//long temp = 0, up_difference = 0, down_difference = 0, left_difference = 0, right_difference = 0;
	int beta_current = beta_start;
	int time = 0;
	MatrixXf second_derivative = MatrixXf::Identity(8, 8);
	second_derivative  = second_derivative * 2;
	second_derivative = second_derivative.inverse();
	while (beta_current <= beta_end)
	{
		//計算的D(s)
		/*for (int i = 1; i < image.rows - 1; i++)
		{
			for (int j = 1; j < image.cols - 1; j++)
			{
				up_difference = pow((image.at<float>(i, j) - image.at<float>(i - 1, j)), 2);
				down_difference = pow((image.at<float>(i, j) - image.at<float>(i + 1, j)), 2);
				left_difference = pow((image.at<float>(i, j) - image.at<float>(i, j - 1)), 2);
				right_difference = pow((image.at<float>(i, j) - image.at<float>(i, j + 1)), 2);
				temp = up_difference + down_difference + left_difference + right_difference;
				if (temp < nu / beta_current)
				{
					zeta_value.at<float>(i, j) = 0;
				}
				else
				{
					zeta_value.at<float>(i, j) = temp;
				}
			}
		}*/
		MatrixXf first_derivative(8, 1);
		for (int i = 1; i < roberts_img.rows - 1; i++)
		{
			for (int j = 1; j < roberts_img.cols - 1; j++)
			{
				first_derivative(0, 0) = 2 * (roberts_img.at<short>(i - 1, j - 1) - roberts_img.at<short>(i, j));
				first_derivative(1, 0) = 2 * (roberts_img.at<short>(i - 1, j) - roberts_img.at<short>(i, j));
				first_derivative(2, 0) = 2 * (roberts_img.at<short>(i - 1, j + 1) - roberts_img.at<short>(i, j));
				first_derivative(3, 0) = 2 * (roberts_img.at<short>(i, j - 1) - roberts_img.at<short>(i, j));
				first_derivative(4, 0) = 2 * (roberts_img.at<short>(i, j + 1) - roberts_img.at<short>(i, j));
				first_derivative(5, 0) = 2 * (roberts_img.at<short>(i + 1, j - 1) - roberts_img.at<short>(i, j));
				first_derivative(6, 0) = 2 * (roberts_img.at<short>(i + 1, j) - roberts_img.at<short>(i, j));
				first_derivative(7, 0) = 2 * (roberts_img.at<short>(i + 1, j + 1) - roberts_img.at<short>(i, j));
				
				MatrixXf direction = second_derivative * first_derivative;
				roberts_img.at<short>(i - 1, j - 1) = roberts_img.at<short>(i - 1, j - 1) - direction(0, 0);
				roberts_img.at<short>(i - 1, j) = roberts_img.at<short>(i - 1, j) - direction(1, 0);
				roberts_img.at<short>(i - 1, j + 1) = roberts_img.at<short>(i - 1, j + 1) - direction(2, 0);
				roberts_img.at<short>(i, j - 1) = roberts_img.at<short>(i, j - 1) - direction(3, 0);
				roberts_img.at<short>(i, j + 1) = roberts_img.at<short>(i, j + 1) - direction(4, 0);
				roberts_img.at<short>(i + 1, j - 1) = roberts_img.at<short>(i + 1, j - 1) - direction(5, 0);
				roberts_img.at<short>(i + 1, j) = roberts_img.at<short>(i + 1, j) - direction(6, 0);
				roberts_img.at<short>(i + 1, j + 1) = roberts_img.at<short>(i + 1, j + 1) - direction(7, 0);
				
			}
		}
		beta_current = beta_current * mu;
		time++;
	}
	Mat smooth_img;
	roberts_img.convertTo(smooth_img, CV_32FC1);
	return smooth_img;
}

展示效果

原始影象

原始的流場

平滑後的流場

原始圖片

原始的流場

平滑後的流場