示例程式碼：

    #include <iostream>
    using namespace std;
    
    int main(){
    	int array[]={1,2,3,4,5};
    	int i=-1;
    	cout<<sizeof(array)<<endl;
    	if(i<=sizeof(array))
    		cout<<"yes";
    	else
    		cout<<"no";
    	return 0;
    } 

結果：

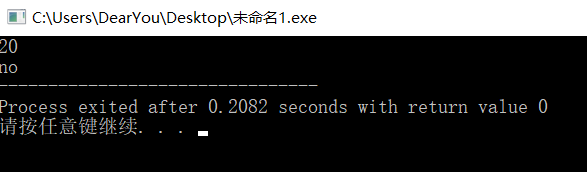
解釋：

sizeof函式返回的值是unsigned型別的，而當unsigned和signed型別的做運算時，signed會被轉化成unsigned型別。 而int i=-1；他的記憶體表示為0xffffffff，當轉化成unsigned後，他的值就變成了2${32}^{}$

教訓

有符合和無符號數混用很危險。儘量減少這種情況，一般使用int型別，如果必須使用unsigned，一定要記得型別轉換。