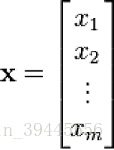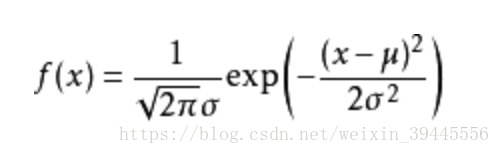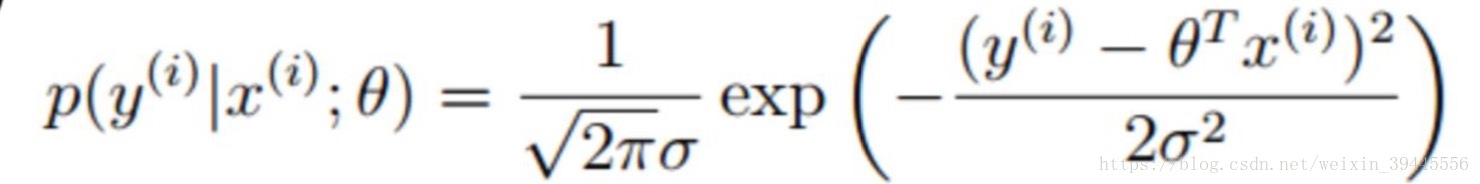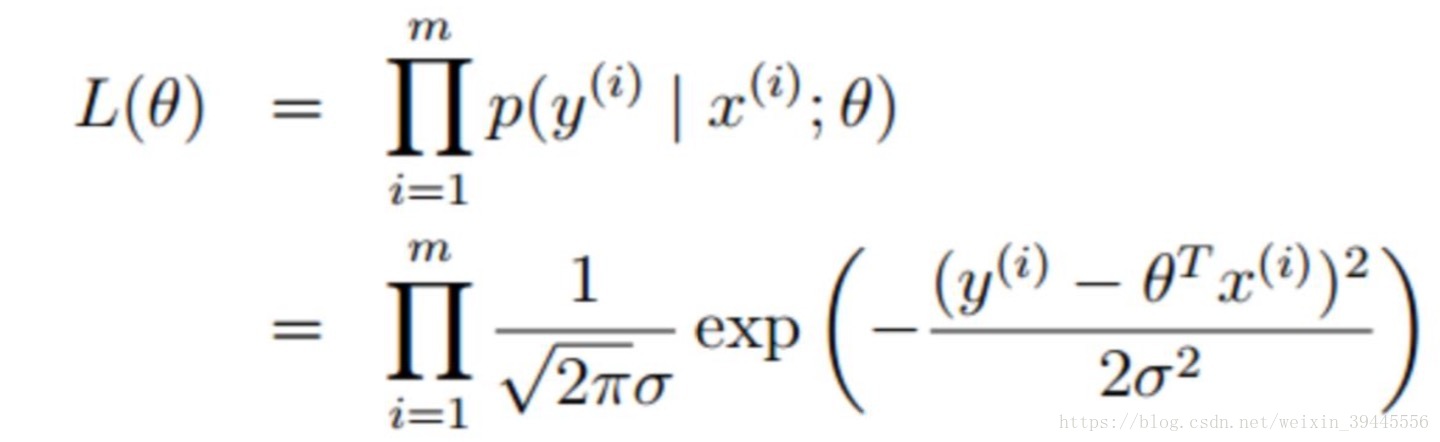常用演算法一   多元線性迴歸詳解1

      此次我們來學習人工智慧的第一個演算法:多元線性迴歸.文章會包含必要的數學知識回顧,大部分比較簡單,數學功底好的朋友只需要瀏覽標題,簡單瞭解需要哪些數學知識即可.

本章主要包括以下內容

        數學基礎知識回顧

        什麼是多元線性迴歸

        多元線性迴歸的推導過程詳解

        如何求得最優解詳解

數學基礎知識回顧

1-截距

      我們知道,y=ax+b這個一元一次函式的影象是一條直線.當x=0時,y=b,所以直線經過點(0,b),我們把當x=0時直線與y軸交點到x軸的距離稱為直線y=ax+b影象在x軸上的截距,其實截距就是這個常數b.(有點拗口,多讀兩遍)

截距在數學中的定義是:直線的截距分為橫截距和縱截距，橫截距是直線與X軸交點的橫座標，縱截距是直線與Y軸交點的縱座標。根據上邊的例子可以看出,我們一般討論的截距預設指縱截距.

2-斜率

     既然已知y=ax+b中b是截距,為了不考慮常數b的影響,我們讓b=0,則函式變為y=ax.

      注意變換後表示式的影象.當a=1時,y=ax的影象是經過原點,與x軸呈45°夾角的直線(第一,三象限的角平分線),當a的值發生變化時,y=ax的影象與x軸和y軸的夾角也都會相應變化,我們稱為這條直線y=ax的傾斜程度在發生變化,又因為a是決定直線傾斜程度的唯一的量(即便b不等於0也不影響傾斜程度),那麼我們就稱a為直線y=ax+b的斜率.

      斜率在數學中的解釋是 表示一條直線(或曲線的切線)關於(橫)座標軸傾斜程度的量.

3-導數

     還是y=ax+b,我們知道這個函式的影象是一條直線,每個不同的x對應著直線上一點y.那麼當自變數x的值變化的時候,y值也會隨之變化.數學中我們把x的變化量成為Δx,把對應的y的變化量成為Δy,自變數的變化量Δx與因變數的變化量Δy的比值稱為導數.記作y'.

     y'=Δx/Δy

常用的求導公式在這部分不涉及,我們用到一個記住一個即可.

4-矩陣和向量

什麼是向量:

         向量就是一個數組.比如[1,2,3]是一個有三個元素的向量.                                           

         有行向量和列向量之分,行向量就是數字橫向排列:X=[1,2,3],列向量是數字豎向排列,如下圖

什麼是矩陣:

          矩陣就是元素是陣列的陣列,也就是多維陣列,比如[[1,2,3],[4,5,6]]是一個兩行三列的矩陣,也叫2*3的矩陣. 行代表內層陣列的個數,列代表內層陣列的元素數.一個矩陣中的所有陣列元素相同.

5-向量的運算:

     一個數乘以一個向量等於這個數同向量中的每個元素相乘,結果還是一個向量.

     2 * [1,2,3] = [2,4,6]

    一個行向量乘以一個列向量,是兩個向量對位相乘再相加,結果是一個實數.

* = 1*1 + 2*2 + 3*3 = 14

附加:轉置

       轉置用數學符號T來表示,比如W向量的轉置表示為.轉置就是將向量或者矩陣旋轉九十度.一個行向量的轉置是列向量,列向量的轉置是行向量.一個m*n的矩陣轉置是n*m的矩陣.

注:以上概念完全是為了讀者能容易理解,並不嚴謹,若想知道上述名詞的嚴謹解釋,請自行百度.

什麼是多元線性迴歸

      我們知道y=ax+b是一元一次方程,y=ax1+bx2+c(1和2是角標,原諒我的懶)是二元一次方程.其中,"次"指的是未知數的最大冪數,"元"指的是表示式中x的個數.那麼"多元"的意思可想而知,就是表示式中x(或者叫自變數,也叫屬性)有很多個.

       當b=0時,我們說y=ax,y和x的大小始終符合y/x=a,影象上任意一點的座標,y值都是x值的a倍.我們把這種橫縱座標始終呈固定倍數的關係叫做"線性".線性函式的影象是一條直線.所以我們知道了多元線性迴歸函式的影象一定也是一條直線.

        現在我們知道了多元線性迴歸的多元和線性,而回歸的概念我們在人工智慧開篇(很簡短,請點搜尋"迴歸"檢視概念)中有講述,所以多元線性迴歸就是:用多個x(變數或屬性)與結果y的關係式 來描述一些雜湊點之間的共同特性.

這些x和一個y關係的影象並不完全滿足任意兩點之間的關係(兩點一線),但這條直線是綜合所有的點,最適合描述他們共同特性的,因為他到所有點的距離之和最小也就是總體誤差最小.

所以多元線性迴歸的表示式可以寫成:

              y= w0x0 + w1x1 + w2x2 + ... + wnxn    (0到n都是下標哦)

       我們知道y=ax+b這個線性函式中,b表示截距.我們又不能確定多元線性迴歸函式中預測出的迴歸函式影象經過原點,所以在多元線性迴歸函式中,需要保留一項常數為截距.所以我們規定   y= w0x0 + w1x1 + w2x2 + ... + wnxn中,x0=1,這樣多元線性迴歸函式就變成了:   y= w0 + w1x1 + w2x2 + ... + wnxn,w0項為截距.

      如果沒有w0項,我們   y= w0x0 + w1x1 + w2x2 + ... + wnxn就是一個由n+1個自變數所構成的影象經過原點的直線函式.那麼就會導致我們一直在用一條經過原點的直線來概括描述一些雜湊點的分佈規律.這樣顯然增大了局限性,造成的結果就是預測出的結果函式準確率大幅度下降.

         有的朋友還會糾結為什麼是x0=1而不是x2,其實不管是哪個自變數等於1,我們的目的是讓函式   y= w0x0 + w1x1 + w2x2 + ... + wnxn程式設計一個包含常數項的線性函式.選取任何一個x都可以.選x0是因為他位置剛好且容易理解.

多元線性迴歸的推導過程詳解

1-向量表達形式

        我們前邊回顧了向量的概念,向量就是一個數組,就是一堆數.那麼表示式y= w0x0 + w1x1 + w2x2 + ... + wnxn是否可以寫成兩個向量相乘的形式呢?讓我們來嘗試一下.

        假設向量W= [w1,w2...wn]是行向量,向量X= [x1,x2...xn],行向量和列向量相乘的法則是對位相乘再相加, 結果是一個實數.符合我們的逾期結果等於y,所以可以將表示式寫成y=W * X.

         但是設定兩個向量一個是行向量一個是列向量又容易混淆,所以我們不如規定W和X都為列向量.所以表示式可以寫成 (還是行向量)與向量X相乘.所以最終的表示式為:

         y= * X,其中 也經常用 θ(theta的轉置,t是上標)表示.

         此處,如果將兩個表示式都設為行向量,y=W * 也是一樣的,只是大家為了統一表達形式,選擇第一種形式而已.

2-最大似然估計

       最大似然估計的意思就是最大可能性估計,其內容為:如果兩件事A,B相互獨立,那麼A和B同時發生的概率滿足公式

              P(A | B) = P(A) * P(B)

        P(x)表示事件x發生的概率.

        如何來理解獨立呢?兩件事獨立是說這兩件事不想關,比如我們隨機抽取兩個人A和B,這兩個人有一個共同特性就是在同一個公司,那麼抽取這兩個人A和B的件事就不獨立,如果A和B沒有任何關係,那麼這兩件事就是獨立的.

        我們使用多元線性迴歸的目的是總結一些不想關元素的規律,比如以前提到的雜湊點的表示式,這些點是隨機的,所以我們認為這些點沒有相關性,也就是獨立的.總結不相關事件發生的規律也可以認為是總結所有事件同時發生的概率,所有事情發生的概率越大,那麼我們預測到的規律就越準確.

這裡重複下以前我們提到的觀點.迴歸的意思是用一條直線來概括所有點的分佈規律,並不是來描述所有點的函式,因為不可能存在一條直線連線所有的雜湊點.所以我們計算出的值是有誤差的,或者說我們迴歸出的這條直線是有誤差的.我們迴歸出的這條線的目的是用來預測下一個點的位置.

        考慮一下,一件事情我們規律總結的不準,原因是什麼?是不是因為我們觀察的不夠細或者說觀察的維度不夠多呢?當我們擲一個骰子,我們清楚的知道他擲出的高度,落地的角度,反彈的力度等等資訊,那上帝視角的我們是一定可以知道他每次得到的點數的.我們觀測不到所有的資訊,所以我們認為每次投骰子得到的點數是不確定的,是符合一定概率的,未觀測到的資訊我們稱為誤差.

        一個事件已經觀察到的維度發生的概率越大,那麼對應的未觀測到的維度發生的概率就會越小.可以說我們總結的規律就越準確.根據最大似然估計

        P(y) = P(x1,x2 ... xn)= P(x1) * P(x2) ... P(xn)

       當所有事情發生的概率為最大時,我們認為總結出的函式最符合這些事件的實際規律.所以我們把總結這些點的分佈規律問題轉變為了 求得P(x1,x2 ... xn)= P(x1) * P(x2) ... P(xn)的發生概率最大.

3-概率密度函式

       數學中並沒有一種方法來直接求得什麼情況下幾個事件同時發生的概率最大.所以引用概率密度函式.

       首先引入一點概念:

               一個隨機變數發生的概率符合高斯分佈(也叫正太分佈).此處為單純的數學概念,記住即可.

               高斯分佈的概率密度函式還是高斯分佈.公式如下:

                公式中x為實際值,u為預測值.在多元線性迴歸中,x就是實際的y,u就是θ * X.

       既然說我們要總結的事件是相互獨立的,那麼這裡的每個事件肯定都是一個隨機事件,也叫隨機變數.所以我們要歸納的每個事件的發生概率都符合高斯分佈.

       什麼是概率密度函式呢?它指的就是一個事件發生的概率有多大,當事件x帶入上面公式得到的值越大,證明其發生的概率也越大.需要注意,得到的並不是事件x發生的概率,而只是知道公式的值同發生的概率呈正比而已.

       如果將y= θ * X中的每個x帶入這個公式,得到如下函式

       求得所有的時間發生概率最大就是求得所有的事件概率密度函式結果的乘積最大,則得到:

         求得最大時W的值,則總結出了所有事件符合的規律.求解過程如下(這裡記住,我們求得的是什麼情況下函式的值最大,並不是求得函式的解):

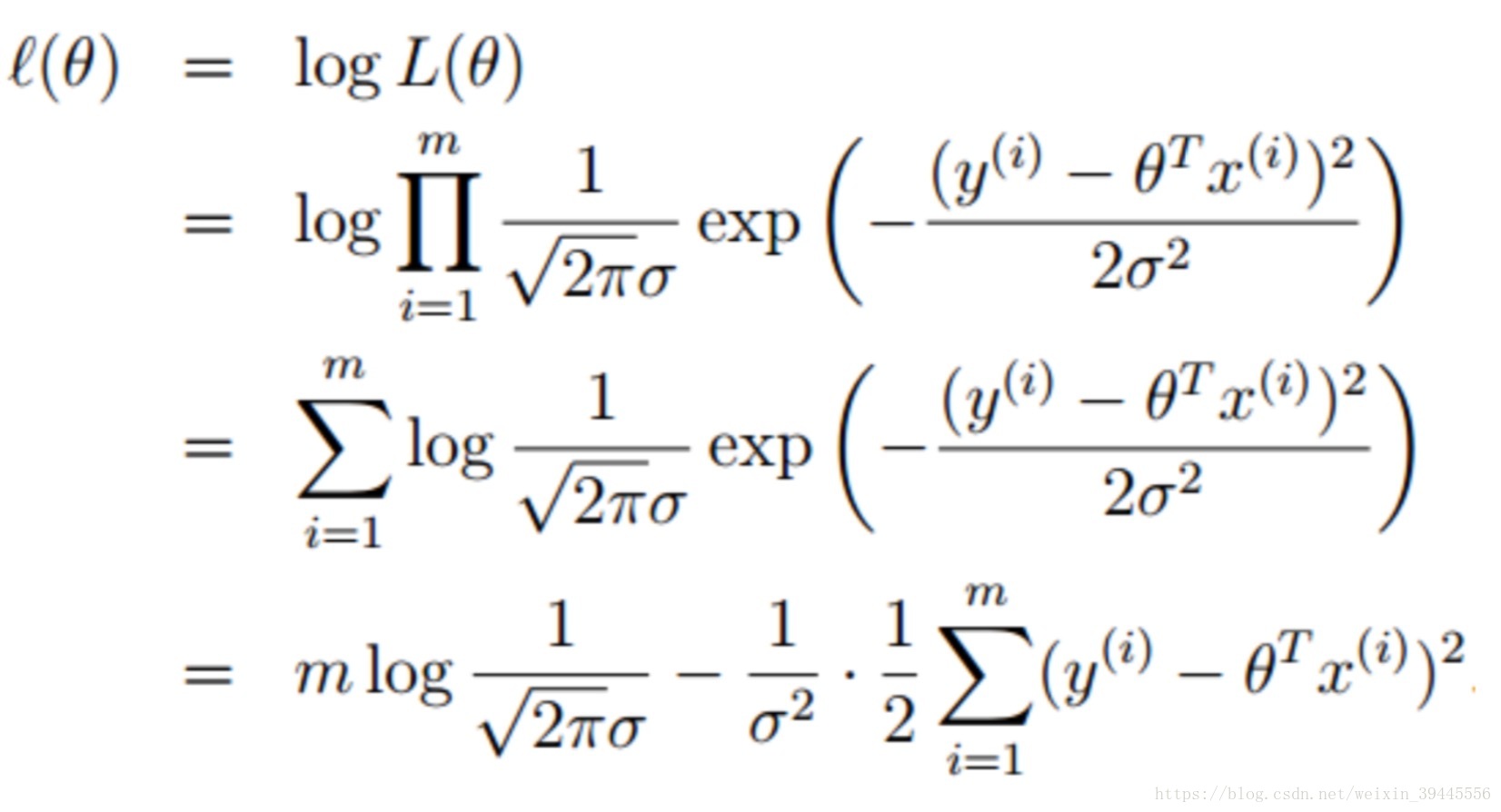
           公式中,m為樣本的個數,π和σ為常數,不影響表示式的大小.所以去掉所有的常數項得到公式:

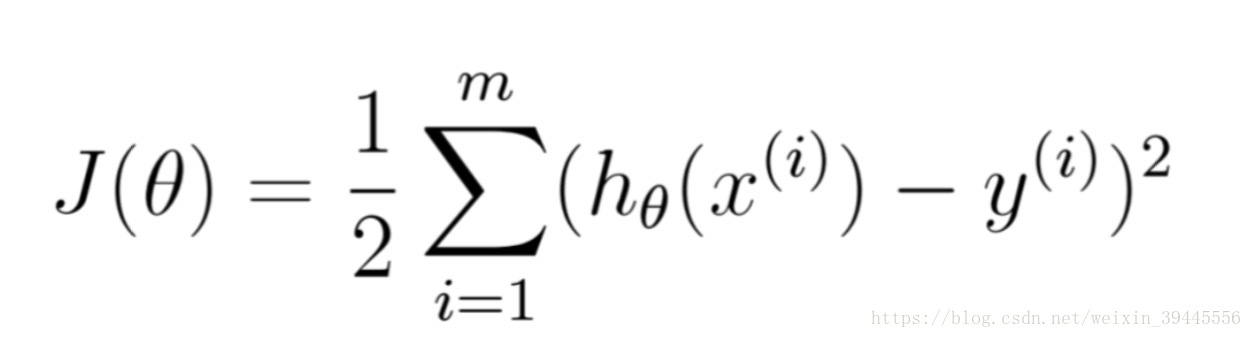
           因為得到的公式是一個常數減去這個公式,所以求得概率密度函式的最大值就是求得這個公式的最小值.這個公式是一個數的平方,在我國數學資料中把他叫做最小二乘公式.所以多元線性迴歸的本質就是最小二乘.

到這裡,多元線性迴歸的推導過程就結束了,後邊會繼續寫如何求解多元線性迴歸.有哪裡寫的不清楚請大家留言.看到一定會回覆的.