【GANs學習筆記】(九)WGAN-GP
6.1 WGAN-GP原理
WGAN待解決的問題是,未能將D真的限制在1-Lipschitz function內。我們不妨觀察一下1-Lipschitz function,會發現它其實等價於如下表達式:
![]()
也就是說,對於一個可微函式,當且僅當對於任意的x,梯度的模都小於或等於1,則該可微函式是1-Lipschitz function。
那現在我們對discriminator的目標表達式增添一個條件:
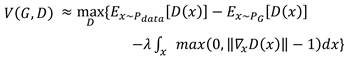
增添的條件(第三項),實際上統計的就是所有梯度的模不滿足小於或等於1的項,給這些項分配一個懲罰引數λ,計算出懲罰值,並將所有懲罰值累加起來。當這個累加懲罰夠大時,它會拖累![]() 的取值,最終導致這樣的D
的取值,最終導致這樣的D
但是,這個增添的條件由於對所有x有效,會讓懲罰變得非常高,也帶來很多不必要的計算,於是我們需要對新增條件做進一步的更改。
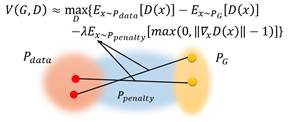
事實上我們真正需要考慮的懲罰項,應該是對discriminator產生實質影響的區域。考慮到整個WGAN的目的是讓![]() 漸漸向
漸漸向![]() 靠攏,那位於
靠攏,那位於![]() 和
和![]() 之間的區域一定會對discriminator產生實質的影響。因此,我們將懲罰項中x的範圍縮小為
之間的區域一定會對discriminator產生實質的影響。因此,我們將懲罰項中x的範圍縮小為![]() ,
,![]() 是介於
是介於![]() 和
和![]() 之間的區域。目標表達式轉化為如下式子:
之間的區域。目標表達式轉化為如下式子:
當然,我們只是直觀上覺得,將懲罰項x的區域縮小為![]() 會對於限制D為1-Lipschitz function有效,那有沒有理論證明呢?很遺憾,原論文中是沒有的,作者寫了這樣一段話:“Given that enforcing the Lipschitz constraint everywhere is
intractable, enforcing it only along these straight lines seems sufficient and
experimentally results in good performance.”
會對於限制D為1-Lipschitz function有效,那有沒有理論證明呢?很遺憾,原論文中是沒有的,作者寫了這樣一段話:“Given that enforcing the Lipschitz constraint everywhere is
intractable, enforcing it only along these straight lines seems sufficient and
experimentally results in good performance.”
還有一個有意思的一點是,在實驗中作者發現![]() 越接近1,訓練得越快,效果也越好,於是不妨把表示式直接改成:
越接近1,訓練得越快,效果也越好,於是不妨把表示式直接改成:
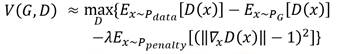
也就是說,在懲罰項中希望![]() 越接近1,懲罰就越少。事實證明這樣做的效果是非常好的。
越接近1,懲罰就越少。事實證明這樣做的效果是非常好的。
綜上WGAN-GP的介紹到這就結束了,它的核心突破,在於用gradient penalty實現了對discriminator的近似1-Lipschitz限制,並且在實驗中取得了非常不錯的效果。
6.2 WGAN-GP的討論
很明顯,WGAN-GP它依然有值得改進的空間。
舉一個例子,如下圖:

我們認為,把![]() 和
和![]() 之間的區域看作
之間的區域看作![]() 是因為它是會產生影響的,但是在上圖中,
是因為它是會產生影響的,但是在上圖中,![]() 和
和![]() 連線的區域對於
連線的區域對於![]()
![]() 真正的走向應該是朝著更近的
真正的走向應該是朝著更近的![]() 去變化,而不是朝著上圖的這條連線去變成一個更遠的
去變化,而不是朝著上圖的這條連線去變成一個更遠的![]() 。
。
也有一些paper試圖在解決這些問題,譬如DRAGAN就認為,![]() 應該還加入
應該還加入![]() 區域,等等。
區域,等等。
另外,WGAN-GP還有一個問題,就是它只是對於梯度的模大於1的區域的x作出了懲罰,它並沒有保證每一個x的梯度的模都小於或等於1,也就是說它並沒有從根本上解決discriminator的1-Lipschitz限制問題。那有沒有辦法能夠保證每個區域上的x的梯度的模都小於等於1呢?有。接下來將在下一章介紹Spectral NormalizationGAN方法。
