【GANs學習筆記】(十)SNGAN
7.1 SNGAN設計思路
現在我們的目的,是要保證對於每一個位置的x,梯度的模都小於等於1。在神經網路中,將梯度的模限制在一個範圍內,抽象地來說就是讓產生的函式更平滑一些,最常見的做法便是正則化。SNGAN(頻譜歸一化GAN)為了讓正則化產生更明確地限制,提出了用譜範數標準化神經網路的引數矩陣W,從而讓神經網路的梯度被限制在一個範圍內。
7.2 頻譜範數
我們先以前饋神經網路為一個簡單的例子來解釋頻譜範數(下稱譜範數)的作用。(7.2-7.4節是一些相關的理論基礎,如果不感興趣可以直接跳到7.5節)
一個前饋神經網路可以表示為級聯計算:![]() 。其中
。其中![]() 代表層數,
代表層數,![]() ;
;![]() 是第
是第![]() 層的輸入,
層的輸入,![]() 是第
是第![]() 層的輸出,
層的輸出,![]() 是一個(非線性的)啟用函式,
是一個(非線性的)啟用函式,![]()
![]() 分別代表
分別代表![]() 層的權重矩陣和偏置向量。現在我們把全體引數的集合記作Θ,Θ=
層的權重矩陣和偏置向量。現在我們把全體引數的集合記作Θ,Θ=![]() ;全體網路層所形成的函式記作
;全體網路層所形成的函式記作![]() ,即有:
,即有:![]() 。給定K組訓練資料,
。給定K組訓練資料,![]() ,損失函式定義為:
,損失函式定義為:![]() ,通常L被選擇為交叉熵或是
,通常L被選擇為交叉熵或是![]() 距離,分別用於分類和迴歸任務。要學習的模型引數是Θ。
距離,分別用於分類和迴歸任務。要學習的模型引數是Θ。
現在我們開始考慮如何獲得對輸入的擾動不敏感的模型。
我們的目標是獲得一個模型Θ,使得f(x +ξ)-f(x)的模(指的是2-範數,即各個元素的平方和)很小,其中ξ是具有小的模的擾動向量。假設我們選用的啟用函式是ReLU或maxout等分段線性函式,在這種情況下,![]() 也是分段線性函式。 因此,如果我們考慮x的小鄰域,我們可以將
也是分段線性函式。 因此,如果我們考慮x的小鄰域,我們可以將![]() 視為線性函式。 換句話說,我們可以用仿射對映表示它,
視為線性函式。 換句話說,我們可以用仿射對映表示它,![]()
![]() 是矩陣,
是矩陣,![]() 是向量,它們都取決於Θ和x的值。 然後,對於小擾動ξ,我們有:
是向量,它們都取決於Θ和x的值。 然後,對於小擾動ξ,我們有:
![]()
其中σ![]() 就是
就是![]() 的譜範數的計算式,數學上它等價於計算矩陣
的譜範數的計算式,數學上它等價於計算矩陣![]() 的最大奇異值(奇異值的介紹見7.2節)。矩陣最大奇異值的表示式參見下式:
的最大奇異值(奇異值的介紹見7.2節)。矩陣最大奇異值的表示式參見下式:
![]()
上述論證表明我們應當訓練模型引數Θ,使得對於任何x,![]() 的譜範數都很小。 為了進一步研究
的譜範數都很小。 為了進一步研究![]() 的性質,讓我們假設每個啟用函式
的性質,讓我們假設每個啟用函式![]() 都是ReLU(該引數可以很容易地推廣到其他分段線性函式)。注意,對於給定的向量x,
都是ReLU(該引數可以很容易地推廣到其他分段線性函式)。注意,對於給定的向量x,![]() 充當對角矩陣
充當對角矩陣![]() ,其中如果
,其中如果![]() 中的對應元素為正,則對角線中的元素等於1; 否則,它等於零(這是ReLU的定義)。於是,我們可以重寫
中的對應元素為正,則對角線中的元素等於1; 否則,它等於零(這是ReLU的定義)。於是,我們可以重寫![]() 為下式:
為下式:
![]()
又注意到對於每個![]() ,有σ
,有σ![]() ≤1,所以我們有:
≤1,所以我們有:
![]()
至此我們得出了一個非常重要的結論,為了限制![]()
![]() 限制
限制![]() 的譜範數就足夠了。這促使我們考慮譜範數正則化,這將在7.3節中描述。
的譜範數就足夠了。這促使我們考慮譜範數正則化,這將在7.3節中描述。
7.3* 奇異值與奇異值分解
在介紹頻譜範數正則化之前,先簡要介紹一下後面會用到的技巧:奇異值分解。奇異值是線性代數中的概念,奇異值分解是矩陣論中一種重要的矩陣分解法,奇異值一般通過奇異值分解定理求得。如果讀者瞭解奇異值的話這一節可以跳過。
奇異值的定義
設A為m*n矩陣,q=min(m,n),A*A的q個非負特徵值的算術平方根叫作A的奇異值。
奇異值分解定理
設給定 ![]() ,令
,令 ![]() ,並假設
,並假設 ![]() :
:
(a) 存在酉矩陣 ![]() 與
與 ![]() ,以及一個對角方陣
,以及一個對角方陣
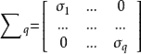
使得![]() 以及
以及 ![]() ,
,
其中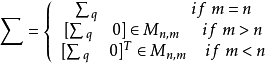
(b) 引數 ![]() 是
是 ![]() 的按照遞減次序排列的非零特徵值的正的平方根,它們與
的按照遞減次序排列的非零特徵值的正的平方根,它們與![]() 的按照遞減次序排列的非零特徵值的正的平方根是相同的。
的按照遞減次序排列的非零特徵值的正的平方根是相同的。
在奇異值分解定理中,矩陣 ![]() 的對角元素(即純量
的對角元素(即純量![]() ,它們是方陣
,它們是方陣 ![]() 的對角元素)稱為矩陣A的奇異值。
的對角元素)稱為矩陣A的奇異值。
*奇異值分解定理的證明
證明比較複雜,在此不贅述了,推薦一篇博文,感興趣的讀者可以去了解一下:
但是要注意的是,7.3節當中提到了一些概念,其中左奇異向量指的是![]() 的特徵向量,右奇異向量指的是
的特徵向量,右奇異向量指的是![]() 的特徵向量。
的特徵向量。
7.4 頻譜範數正則化
頻譜範數正則化方法是17年5月提出來的,雖然最終的SNGAN沒有完全採用這一方法,但是它借鑑了這個方法非常重要的思想。
為了約束每個權重矩陣的頻譜範數![]() ,我們考慮以下經驗風險最小化問題:
,我們考慮以下經驗風險最小化問題:
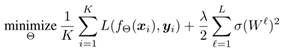
其中λ∈![]() 是正則化因子,第二項被稱為譜範數正則項,它降低了權重矩陣的譜準則。
是正則化因子,第二項被稱為譜範數正則項,它降低了權重矩陣的譜準則。
在執行標準梯度下降時,我們需要計算譜範數正則項的梯度。為此,讓我們考慮對於一個特定![]() 的梯度σ(
的梯度σ(![]() /2,其中
/2,其中![]() 。 設
。 設![]() =σ(
=σ(![]() 和
和![]() 分別是第一和第二奇異值。 如果
分別是第一和第二奇異值。 如果![]() >
>![]() ,則σ(
,則σ(![]() /2的梯度為
/2的梯度為![]() ,其中,
,其中,![]() 和
和![]() 分別是第一個左奇異向量和第一個右奇異向量。 如果
分別是第一個左奇異向量和第一個右奇異向量。 如果![]() =
=![]() ,則σ(
,則σ(![]() /2是不可微的。
然而,出於實際目的,我們可以假設這種情況從未發生,因為實際訓練中的數值誤差會讓
/2是不可微的。
然而,出於實際目的,我們可以假設這種情況從未發生,因為實際訓練中的數值誤差會讓![]() 和
和![]() 不可能完全相等。
不可能完全相等。
由於計算![]() ,
,![]() 和
和![]() 在計算上是昂貴的,我們使用功率迭代方法來近似它們。從隨機初始化的v開始(開始於
在計算上是昂貴的,我們使用功率迭代方法來近似它們。從隨機初始化的v開始(開始於![]() 層),我們迭代地執行以下過程足夠次數:
層),我們迭代地執行以下過程足夠次數:
![]()
最終我們得到了使用頻譜範數正則項的SGD演算法如下:

值得注意的是,為了最大化![]() ,
,![]() 和
和![]() ,在SGD的下一次迭代開始時,我們可以用
,在SGD的下一次迭代開始時,我們可以用![]() 代替第2步中的初始向量v。然後在第7步中右方的標註是,paper作者在實驗中發現,只進行一次迭代就能夠獲得足夠好的近似值。文章中還提到對於含有卷積的神經網路架構,我們需要將引數對齊為b×a
代替第2步中的初始向量v。然後在第7步中右方的標註是,paper作者在實驗中發現,只進行一次迭代就能夠獲得足夠好的近似值。文章中還提到對於含有卷積的神經網路架構,我們需要將引數對齊為b×a![]() 的矩陣,再去計算該矩陣的譜範數並新增到正則項中。
的矩陣,再去計算該矩陣的譜範數並新增到正則項中。
綜上,頻譜範數正則化看起來非常複雜,但是它的實際做法,可以簡單地理解為,把傳統GANs中的loss函式:
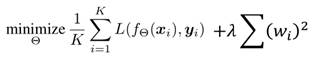
其中的正則項替換成了譜範數:
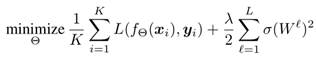
並且譜範數的計算利用了功率迭代的方法去近似。
7.5 SNGAN的實現
之前我們說到,對於GANs最重要的目的是實現D的1-lipschitz限制,頻譜範數正則化固然有效,但是它不能保證把![]() 的梯度限制在一個確定的範圍內,真正解決了這一問題的,是直到18年2月才被提出的SNGAN。SNGAN基於spectral normalization的思想,通過對W矩陣歸一化的方式,真正將
的梯度限制在一個確定的範圍內,真正解決了這一問題的,是直到18年2月才被提出的SNGAN。SNGAN基於spectral normalization的思想,通過對W矩陣歸一化的方式,真正將![]() 的梯度控制在了小於或等於1的範圍內。
的梯度控制在了小於或等於1的範圍內。
我們先來證明,只要將每一層![]() 的譜範數都限制為1,最終得到的
的譜範數都限制為1,最終得到的![]() 函式就會滿足1-lipschitz限制。
函式就會滿足1-lipschitz限制。
對於一個線性層函式g(h)=Wh,我們可以計算出它的lipschitz正規化:
![]()
如果啟用層函式的lipschitz正規化![]() =1(比如ReLU),我們就有如下不等式:
=1(比如ReLU),我們就有如下不等式:
![]()
其中○表示複合函式。我們利用上面的不等式,就能夠得到![]() 的lipschitz正規化的限制式:
的lipschitz正規化的限制式:
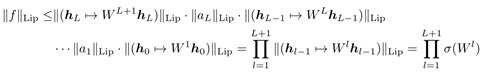
於是現在,我們只需要保證![]() 恆等於1,就能夠讓
恆等於1,就能夠讓![]() 函式滿足1-lipschitz限制。做法非常簡單,只需要將W矩陣歸一化即可:
函式滿足1-lipschitz限制。做法非常簡單,只需要將W矩陣歸一化即可:
![]()
至此,SNGAN通過將W矩陣歸一為譜範數恆等於1的式子,進而控制![]() 的梯度恆小於等於1,最終實現了對D的1-lipschitz限制,最後我們給出SNGAN中的梯度下降演算法:
的梯度恆小於等於1,最終實現了對D的1-lipschitz限制,最後我們給出SNGAN中的梯度下降演算法:

可以看出,與傳統的SGD相比,帶有譜歸一化的SGD做的額外處理就是對W矩陣做的歸一化處理:
![]()
