很多問題都可以暴力解決，不用動太多腦筋，把所有可能性列出來，然後一一試驗。儘管這樣的方法顯得很笨，但卻常常是行之有效的。

有沒有想過如何列印所有排列呢？輸入整數n，按字典序從小到大的順序輸出前n個數的所有排列。前面講過，兩個序列的字典序大小關係等價於從頭開始第一個不相同位置處的大小關係。例如，（1,3,2） < (2,1,3)，字典序最小的排列是(1,2,3,4,...,n)，最大的排列是(n,n-1,n-2,..1).n=3時，所有排列的排序結果是(1,2,3)、（1,3,2,）、（2,1,3）、（2,3,1）、（3,1,2）、（3,2,1）。

生成1-n的排列。

輸入：正整數n

輸出：1-n的全排列。

執行結果：

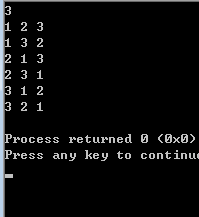
我們可以嘗試用遞迴的思想解決：先輸出所有以1開頭的排列（這一步是遞迴呼叫），然後輸出以2開頭的排列（又是遞迴呼叫），接著是以3開頭的排列....最後才是以n開頭的排列。

以1開頭的排列的特點是i：第一位是1，後面是2-9的排列，根據字典序的定義，這些2-9的排列也必須按照字典序排列。換句話說，需要“按照字典序輸出2-9”的排列，不過需注意的是，在輸出時，每個排列的最前面要加上1，這樣一來，所設計的遞迴函式需要一下引數：

已經確定的字首序列，以便輸出。

需要進行全排列的元素集合，以便依次選做第一個元素。

這樣可得到一個虛擬碼：

void print_permutation(序列A， 集合S)
{
    if(S為空)
        輸出序列A；
    else    按照從小到大的順序依次考慮S的每個元素v
    {
        print_permutation(在A的末尾新增v後得到的新序列，S-{v});
    }
}
 

暫時不用考慮序列A和集合S如何表示，首先理解一下上面的虛擬碼。遞迴邊界是S為空的情形，這很好理解:現在序列A就是一個完整的序列，直接輸出即可，接下來按照從小到大順序考慮S中的每個元素，每次遞迴呼叫以A開頭。

下面考慮程式實現。不難想到用陣列表示序列A，而集合S根本不用儲存，因為它可以由序列A完全確定--A中沒有出現的元素都可以選。C語言中的函式在接受陣列引數時無法得知陣列的元素個數，所以需要傳一個已經填好的位置個數，或者當前需要確定的元素位置cur。

void print_permutation(int n,int *A,int cnt)
{
    //按照字典序從小到大生成1-n的排列
    int i,j;
    if(n==cnt) //遞迴邊界
    {
        for(i=0;i<n;i++)
            printf("%d ",A[i]);
        printf("\n");
    }
    else
    {
        for(i=1;i<=n;i++) //嘗試在A[cur]中填各種整數i
        {
            bool ok=true;
            for(j=0;j<cnt;j++)
                if(A[j]==i) //如果i已經在A[0]-A[cut-1]中出現過，則不能再選
                   ok=false;
            if(ok)
            {
                A[cnt]=i;
                print_permutation(n,A,cnt+1); //遞迴呼叫
            }
        }
    }
}
 

迴圈變數i是當前考察的A[cur]，為了檢查元素i是否已經用過，上面的程式用到了一個標誌變數ok，初始值為1（真），如果發現有某個A[j]==i時，則改為0（假）。如果最終ok仍為1，則說明i沒有在序列中出現過，把它新增到序列末尾(A[cur]=i)後遞迴呼叫。

宣告一個足夠大的陣列A，然後呼叫print_permutation(n,A,0)，即可按字典序輸出1-n的所有排列。

生成可重集的排列。

如果把問題改成：輸入陣列P，並按字典序輸出陣列A各元素的所有全排列，則需要對上述程式進行修改-把P加到print_permutation的引數列表中，然後把程式碼中的if(A[j]==i)和A[cur]=i分別改成if(A[j]==P[i])和A[cur]=P[i]，這樣，只要把P的所有元素按從小到達的順序排序，然後呼叫print_permutation(n,P,A,0)即可。

輸入：陣列P大小n，陣列P中的各個元素。

輸出：陣列P的所有全排列。

執行結果:

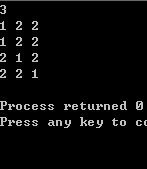
這個方法看上去不錯，可惜有一個小問題：輸入 1 1 1後，程式什麼也不輸出（正確答案應該是唯一的全排列 1 1 1 ）。原因在於，這樣禁止A陣列中出現重複，而在P中本來就有重複元素時，這個禁令是錯誤的。

一個解決方法是統計A[0]-A[cur-1]中P[i]的出現次數c1，以及P陣列中P[i]的出現次數c2，只要c1<c2，就能遞迴呼叫。

else for(int i = 0; i < n; ++i)
{
    int c1 = 0, c2 = 0;
    for(int j = 0; j < cur; ++j)
        if(A[j] == P[i])
            c1++;
    for(int j = 0; j < n; ++j)
        if(P[i] == P[j])
            c2++;
    if(c1 < c2)
    {
        A[cur] = P[i];
        print_permutation(n,P,A,cur1);
    } 
}

結果又如何呢？輸入 1 1 1 ，輸出了27個1 1 1.遺漏沒有了，但是出現了重複：先試著把第一個1作為開頭，遞迴呼叫結束後再嘗試用第2個1作為開頭，遞迴呼叫結束後再嘗試用第3個1作為開頭，再一次遞迴呼叫。可實際上這3個1是相同的，應只遞迴1次，而不是3次。

換句話說，我們列舉的下標i應不重複、不遺漏的取遍所有P[i]值。由於P陣列已經排過序，所以只需檢查P的第一個元素和所有“與前一個元素不相同”的元素，即只需在 "for(i=0; i<n; ++i)"和其後的花括號之前加上 "if(!i || P[i] != P[i-1]" 即可。

執行結果：

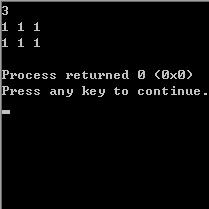
正確的程式碼：

void print_repeat_permutation(int n,int *P,int *A,int cnt)
{
    //輸入陣列P，按照字典序輸出P中各元素的所有全排列，P中元
    //素可以重複
    int i,j,c1,c2;
    if(n==cnt) //遞迴邊界
    {
        for(i=0;i<n;i++)
            printf("%d ",A[i]);
        printf("\n");
    }
    else
    {
        for(i=0;i<n;i++)
        {
            if(!i||P[i]!=P[i-1]) //列舉的下標i應不重複，不遺漏的取遍所有P[i]值
            {
                c1=c2=0;
                for(j=0;j<cnt;j++) //統計i在A中的次數
                   if(A[j]==P[i])
                     c1++;
                for(j=0;j<n;j++) //統計i在P中的次數
                   if(P[j]==P[i])
                     c2++;
                if(c1<c2) //A中次數小於P中次數 遞迴
                {
                   A[cnt]=P[i];
                   print_repeat_permutation(n,P,A,cnt+1);
                }
            }
        }
    }
}