定態薛定諤方程是

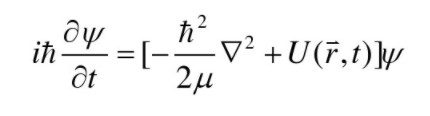
如果是定態的自由粒子，這個方程的解是

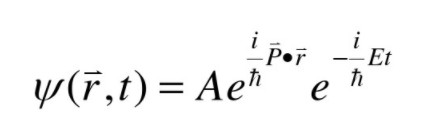
因為是定態的波函式與時間無關，這個粒子的能量E不隨時間變化

假設E=1，讓t→0

所以波函式變成

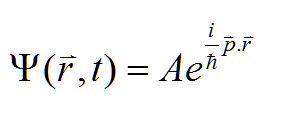
讓A和都等於1

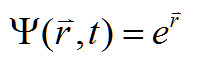
讓神經網路裡的節點都是在位形空間中

 Sigmoid函式在x足夠小的時候可以進行近似的化簡

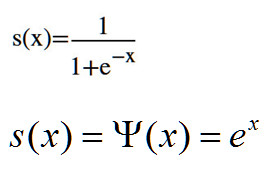
因為已經假定了這是一個定態的自由粒子群

 而且粒子的能量E=1，所以位置X處的電子數量為

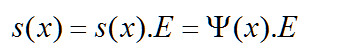
按照波函式的演算法應該用波函式的平方，神經網路這裡和波函式的演算法不同。

按照神經網路的演算法s(x)要乘以權重w，s（x）.W

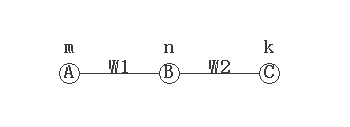
考慮只有3個點的位形空間，乘上一個權重相當於由A點躍遷到B點，想要求出B點電子的數量要知道B點的波函式的平方，而在一個定態環境下波函式只與失徑有關，

所以B點的波函式可以表示為

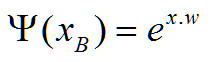
現在讓w的初始化方式為

所以按照神經網路的原理

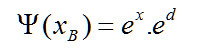
按照波函式的原理

很容易得到

也就是隻要d足夠小神經網路的演算法可以當做波函式演算法的一個近似，按照神經網路的演算法B點的電子數量可以用得到，然後用同樣的方法躍遷到C點。

所以似乎神經網路演算法可以當做定態的自由粒子群之間相互作用的一個近似。

本文參考了百度文庫

《定態薛定諤方程》

https://wenku.baidu.com/view/ed6523285acfa1c7aa00cc86.html