『最小生成樹』Kruskal演算法——加邊法 (並查集優化 + C++語言編寫 + 例題)
『演算法原理』
在一個連通網的所有生成樹中,各邊的代價之和最小的那顆生成樹稱為該連通網的最小代價生成樹(Minimum Cost Spanning Tree),簡稱最小生成樹(MST)。
Kruskal演算法之所以叫加邊法,就是因為其本質是一個邊一個邊地加入到最小生成樹中。
演算法步驟如下:
設有一無向連通圖G,有n個頂點。
- a.將所有邊的權值從小到大排列。
- b.遍歷所有的邊,如果邊加入生成樹後不形成環,則將該邊加入到生成樹中
- c.重複b步驟直至所有頂點都被加入到生成樹中,即生成樹中加入了n-1條邊
下面用圖示來解釋這個過程。
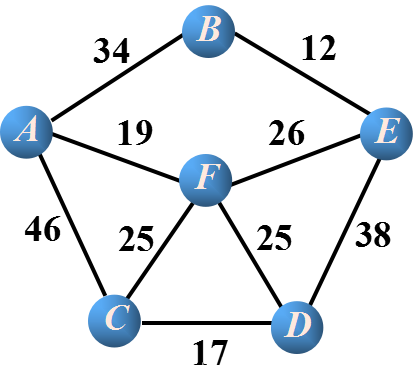
a.將所有的邊從小到大排序
12 19 25 25 26 34 38 46
b.遍歷所有的邊,如果邊加入生成樹後不形成環,則將該邊加入到生成樹中

1).加入權最小的(B,E)
2).加入(C,D)
3).加入(A,F)
3).加入(C,F)
4).加入(F,D),此時發現 F C D形成一個環,不選
5).加入(F,E) 6個點,到此加入了5條邊,生成最小生成樹 演算法結束
在模擬之後,大家就可以發現,Kruskal演算法在程式碼實現時的最大困難在於“如何判斷是否成環”。
模擬的過程中可以發現,n個頂點在初始狀態下可看成n個獨立的連通塊,在不斷加邊的過程中,邊的兩端點會連在一起,形成一個連通塊,故邊的端點在邊加入前
(Vi,Vj為邊的兩端點)
a.Vi,Vj都屬於同一連通塊 例:上圖中,當要加入(F,D)之前,F 和 D都屬於 "A-F-C-D" 這一連通塊
b.Vi,Vj分別屬於不同的連通塊 例:上圖中,當要加入(C,D)之前,C屬於“C”這一連通塊,D屬於“D”這一連通塊
可以看出 a情況下即是成環,故判斷邊的兩端點是否都在同一個連通塊中中,就是判斷是否成環。
這裡引入一個並查集的概念
簡單來說就是在一個連通塊中找出一個頂點作為“根”,同連通塊的其他頂點都是“根”的孩子,如果兩頂點的“根”相同,則兩頂點是在同一連通塊,如果A和B不在同一類中,則將B的“根”變為A的“根”的孩子就可以將A和B歸在同一類。
具體的講解,附上網上流傳的一個通俗的帖子
『模板程式碼』
以上面的圖為測試資料,將原圖中“ABCDEF”的點編號更改為"123456";
/*
a.將所有邊的權值從小到大排列。
b.遍歷所有的邊,如果邊加入生成樹後不形成環,則將權值最小的邊加入到生成樹中
c.重複b步驟直至所有定點都被加入到生成樹中,即生成樹中加入了n-1條
********************************************************
*/
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <algorithm>
using namespace std;
int f[105];
struct Eage{
int v,u,w;//v-起點 u-終點 w-權值
}eage[100];
bool cmp(const Eage& a,const Eage& b){
return a.w < b.w;
}
void Init(){
for(int i = 0; i <= 100; i++)
f[i] = i;
}
int check(int a){//用於查詢到a的"根" 並返回
if(f[a] == a)
return a;
else{
f[a] = check(f[a]);
}
return f[a];
}
bool merger(int a,int b){//將a和b歸併到同一"根"下
int t1 = check(a),t2 = check(b);//先找到a和b的根 t1,t2;
if(t1 == t2){//如果a和b的"根"一樣 成環 返回錯誤
return false;
}else{
f[t2] = f[t1];//如果a和b的"根"不一樣 ,不成環,將a,b歸在同一個"根"下
return true;
}
}
int main(){
int n,tot = 0,sum = 0;
cin>>n;
int a,b,c;
Init();
for(int i = 1; i <= n; i++){
cin>>a>>b>>c;
eage[i].v = a;
eage[i].u = b;
eage[i].w = c;
}
sort(eage+1,eage+n+1,cmp);//a.將所有邊的權值從小到大排列。
cout<<"權值從小到大排列序列如下:\n";
for(int i = 1; i <= n;i++){
cout<<eage[i].w <<" ";
}
cout<<"\n加入的邊為:\n";
for(int i = 1; i <= n; i++){
if(merger(eage[i].v,eage[i].u))//如果不成環,加入到生成樹中 成環就跳過
{
cout<<"("<<eage[i].v<<","<<eage[i].u<<") ";
sum = sum+eage[i].w;
tot++;
if(tot == n-1)
break;
}
}
cout<<"\n最小權值為:"<<sum;
return 0;
} 執行結果:

『例題一道』
【洛谷】P2872 [USACO07DEC]道路建設Building Roads
Farmer John最近得到了一些新的農場,他想新修一些道路使得他的所有農場可以經過原有的或是新修的道路互達(也就是說,從任一個農場都可以經過一些首尾相連道路到達剩下的所有農場)。有些農場之間原本就有道路相連。 所有N(1 <= N <= 1,000)個農場(用1..N順次編號)在地圖上都表示為座標為(X_i, Y_i)的點(0 <= X_i <= 1,000,000;0 <= Y_i <= 1,000,000),兩個農場間道路的長度自然就是代表它們的點之間的距離。現在Farmer John也告訴了你農場間原有的M(1 <= M <= 1,000)條路分別連線了哪兩個農場,他希望你計算一下,為了使得所有農場連通,他所需建造道路的最小總長是多少。
輸入輸出格式
輸入格式:
-
第1行: 2個用空格隔開的整數:N 和 M
-
第2..N+1行: 第i+1行為2個用空格隔開的整數:X_i、Y_i
-
第N+2..N+M+2行: 每行用2個以空格隔開的整數i、j描述了一條已有的道路, 這條道路連線了農場i和農場j
輸出格式:
輸出使所有農場連通所需建設道路的最小總長,保留2位小數,不必做 任何額外的取整操作。為了避免精度誤差,計算農場間距離及答案時 請使用64位實型變數
輸入輸出樣例
輸入樣例#1:
4 1
1 1
3 1
2 3
4 3
1 4輸出樣例#1:
4.00
解題思路:
將所有的頂點連線起來,補成一個完全圖,n個頂點有共n*(n-1)/2條邊。將題目中已存在的邊(本來就有的路)的權值賦為0, 然後使用Kruskal演算法生成最小生成樹。
圖示:
a.將所有頂點補成完全圖

b.將已經存在的邊(原本就有的路)權值賦為0

c.進行Kruskal演算法

下面直接上程式碼:
/*
解題思路:
將原圖補連成一個完全圖,n個頂點有共n*(n-1)/2條邊 將本存在的邊的權值賦為0 然後Kruskal演算法
************************
*/
#include <iostream>
#include <cstdio>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
int f[1010];
struct Node {//點結構體
int x,y;
} node;
struct Eage {//邊結構體
int v,u;
double w;
} e;
vector<Node> vex;
vector<Eage> eage;
bool cmp(const Eage&a,const Eage&b){//排序函式
return a.w < b.w;
}
void Init() {//初始化
for(int i = 1; i <= 1005; i++)
f[i] = i;
}
double Getdis(double x1,double y1,double x2,double y2) {//計算距離函式
double x = abs(x2-x1);
double y = abs(y2-y1);
return sqrt(x*x+y*y);
}
int check(int a){//查詢到a的"根" 並返回
if(f[a] == a)
return a;
else{
f[a] = check(f[a]);
}
return f[a];
}
bool merger(int a,int b){//將a和b歸併到同一"根"下
int t1 = check(a),t2 = check(b);
if(t1 == t2){
return false;
}else{
f[t2] = f[t1];
return true;
}
}
int main() {
//輸入資料
double n,m,sum = 0;
cin>>n>>m;
Init();
for(int i = 1; i <= n; i++) {
cin>>node.x>>node.y;
vex.push_back(node);
}
int a,b;
for(int i = 1; i <= n; i++) {
for(int j = i+1; j <= n; j++) {
e.v = i;
e.u = j;
e.w = Getdis(vex[i-1].x,vex[i-1].y,vex[j-1].x,vex[j-1].y);
eage.push_back(e);
}
}
for(int i =1; i <= m; i++) {//這個地方原本打算將本身就存在邊的權值改為0,後來發現過於繁瑣.
//直接將賦值為0的新邊加到vector後,在判斷是否成環的時候,直接就
//會跳過舊的邊
cin>>a>>b;
e.v = a;e.u = b;e.w = 0;
eage.push_back(e);
}
int len = eage.size();
sort(eage.begin(),eage.end(),cmp);//排序
int tot = 0;
for(int i = 0; i < len; i++){
if(merger(eage[i].v,eage[i].u))//如果不成環,加入到生成樹中
{
sum = sum+eage[i].w;
tot++;
if(tot == n-1){
printf("%.2f",sum);//注意格式
break;
}
}
}
return 0;
}