在日常生活中解決問題經常需要考慮最優的問題，而最小生成樹就是其中的一種。看了很多部落格，先總結如下，只需要您20分鐘的時間，就能完全理解。

比如：有四個村莊要修四條路，讓村子能兩兩聯絡起來，這時就有最優的問題，怎樣修才是做好的，如下圖：第一個是網全圖，後三個圖的修路方案都可以

1.樹的定義：有n個頂點和n-1條邊，沒有迴路的稱為樹

生成樹的定義：生成樹就是包含全部頂點，n-1（n為頂點數）條邊都在圖裡就是生成樹

最小：指的是這些邊加起來的權重之和最小

2.判定條件：向生成樹中任加一條邊都一定構成迴路

充分必要條件：最小生成樹存在那麼圖一定是連通的，反過來，圖是連通的則最小生成樹一定存在

3.和最小生成樹有關的兩個演算法：prim演算法和kruskal演算法

a)prim演算法——讓小樹慢慢長大型演算法

按照樹的定義，一個頂點就是一棵樹。

原理：

1）我們選擇一個頂點，也就是選擇了一個樹。

2）向外找權重最小的邊，這樣這棵樹就有了兩個頂點

3）再以這兩個頂點向外找權重最小的邊，依次迴圈，知道所有頂點收到樹裡

舉例：

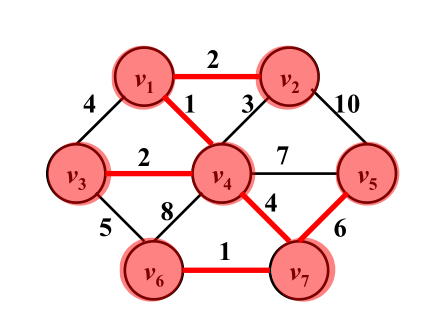
第一步：選擇V1作為頂點

第二步：對比一下與V1相連的各條邊的權重，選擇最小的V1-V4這條邊

第三步：以V1和V4為樹，向外找權重最小的邊，這時就有了V1-V2,V4-V3兩條邊，這樣就把頂點V2和V3收進了樹裡。

接著以V1,V2,V3,V4為頂點的樹，向外選權值最小的邊，注意不能構成迴路。依次迴圈，這樣就選擇了V4-V7,V7-V5,V7-V6這三條邊

數一下現在已經包含了全部的7的頂點，和6條邊了，這樣最小生成樹就長大了

b)kruskal演算法——將森林合併為樹

原理：

1）和prim演算法不一樣的是，kruskal演算法先選擇權重最小的邊（因為一個頂點就是一棵樹，那麼一個邊兩個頂點就可以看成是一棵樹）

2）接著選擇剩下的權值比較小的邊，注意不能形成迴路，只到包含全部頂點

舉例：

還是上面那幅圖

第一步：先選擇V1-V4,V6-V7兩條權值為1的邊

第二步：選擇V4-V3,V1-V2兩條權值為2的邊。接著不能選擇V4-V2權值為3的邊，這樣就構成了迴路，只能選擇V4-V7權值為4的邊。

同理不能選擇V6-V5權值為5的邊，因為會構成迴路，只能選擇V7-V5權值為6的邊。

此時就已經包含了全部的7的頂點，和6條邊了，這樣最小生成樹就從森林變成了樹