2. 程式人生 > >機器學習實戰——SVD（奇異值分解）

機器學習實戰——SVD（奇異值分解）

阿新 • • 發佈：2018-12-18

與PCA一樣的學習過程，在學習SVD時同樣補習了很多的基礎知識，現在已經大致知道了PCA的應用原理，SVD個人感覺相對要難一點，但主要步驟還是能勉強理解，所以這裡將書本上的知識和個人的理解做一個記錄。主要關於（SVD原理、降維公式、重構原矩陣、SVD的兩個實際應用），當然矩陣的分解和相對的公式我會給出寫的更好的文章對於說明（個人基礎有限）。

（最後給出兩條SVD最重要的公式）

SVD（奇異值分解）：

  1. 優點：簡化資料，去除噪聲點，提高演算法的結果；
  2. 缺點：資料的轉換可能難以理解；
  3. 適用於資料型別：數值型。

    通過SVD對資料的處理，我們可以使用小得多的資料集來表示原始資料集，這樣做實際上是去除了噪聲和冗餘資訊，以此達到了優化資料、提高結果的目的。

    隱形語義索引：最早的SVD應用之一就是資訊檢索，我們稱利用SVD的方法為隱性語義檢索（LSI）或隱形語義分析（LSA）

    推薦系統：SVD的另一個應用就是推薦系統，較為先進的推薦系統先利用SVD從資料中構建一個主題空間，然後再在該空間下計算相似度，以此提高推薦的效果。

SVD與PCA不同，PCA是對資料的協方差矩陣進行矩陣的分解，而SVD是直接在原始矩陣上進行的矩陣分解。並且能對非方陣矩陣分解，得到左奇異矩陣U、sigma矩陣Σ、右奇異矩陣VT。

奇異性分解可以將一個矩陣Data_{m\times n}分解成3個矩陣U_{m\times m}、\Sigma_{m\times n}、V_{n\times n}^{T}，其中U、VT都是單式矩陣（unitary matrix），Σ是一個對角矩陣，也就是說只有對角線有值。對角元素稱為奇異值，它們對應了原始矩陣Data的奇異值，如下：

[[2 0 0]  [0 3 0]  [0 0 4]  [0 0 0]]

一般奇異值我們只選擇某一部分，選擇的規則很多種，主要的一種為：

選擇奇異值中佔總奇異值總值90%的那些奇異值。（下面有演示如何選擇）

SVD分解公式如下（類似於因式分解）：

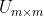
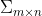
    Data_{m\times n} = U_{m\times m} \Sigma_{m\times n} V_{n\times n}^{T}

圖形化表示奇異值分解：

在PCA中我們根據協方差矩陣得到特徵值，它們告訴我們資料集中的重要特徵，Σ中的奇異值亦是如此。奇異值和特徵值是有關係的，這裡的奇異值就是矩陣Data * Data^{T}特徵值的平方根。

SCV實現的相關線性代數，但我們無需擔心SVD的實現，在Numpy中有一個稱為線性代數linalg的線性代數工具箱能幫助我們。下面演示其用法對於一個簡單的矩陣：

[[1 1]  [1 7]]

from numpy import *
from numpy import linalg as la

df = mat(array([[1,1],[1,7]]))
U,Sigma,VT = la.svd(df)
print(U)
# [[ 0.16018224  0.98708746]
#  [ 0.98708746 -0.16018224]]
print(Sigma)
# [7.16227766 0.83772234]
print(VT)
# [[ 0.16018224  0.98708746]
#  [ 0.98708746 -0.16018224]]

通過簡單的使用該工具就能得到運算的結果，所以我們著重應該理解的應該是這些結果的含義以及後續對它們的使用，下面通過推薦系統這個示例來進行實際的操作（資料集降維、重構資料集）。

基於協同過濾的搜尋引擎：

    我之前在集體程式設計智慧中學習了該演算法，大致有兩種方法來實現：

  1. 基於使用者的協作型過濾
  2. 基於物品的協作型過濾

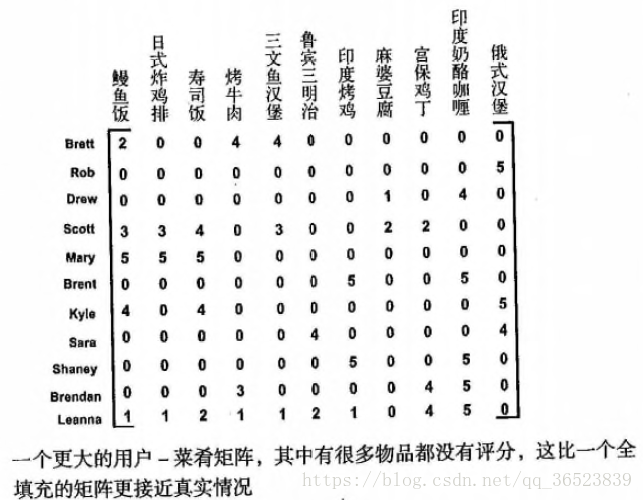
兩種方法大致相同，但是在不同的環境下，使用最佳的方法能最大化的提升演算法的效果。如下圖（後面的示例資料）所示，對兩樣商品直接的距離進行計算，這稱為基於物品的相似度。而對行與行（使用者之間）進行距離的計算，這稱為基於使用者的相似度。到底該選用那種方法呢？這取決與使用者或物品的數量，基於物品相似度的計算時間會隨著物品數量的增加而增加。基於使用者相似度則取決於使用者數量，例如：一個最大的商店擁有大概100000種商品，而它的使用者可能有500000人，這時選擇基於物品相似度可能效果好很多。

用上面的資料解釋瞭如何選擇基於協同過濾，下面使用基於物品相似度的方法來構建推薦系統（先直接使用原始矩陣來構建，然後再將處理函式換為SVD的處理函式，以便作比較）。

（說明：資料間的距離計算採用餘玄相似、歐式距離、皮爾遜相關度其中任一種，這裡不再解釋，提供連結自行學習）

程式碼：

from numpy import *
from numpy import linalg as la

# （使用者x商品）    # 為0表示該使用者未評價此商品，即可以作為推薦商品
def loadExData():
    return [[0, 0, 0, 2, 2],
            [0, 0, 0, 3, 3],
            [0, 0, 0, 1, 1],
            [1, 1, 1, 0, 0],
            [2, 2, 2, 0, 0],
            [5, 0, 5, 0, 0],
            [1, 1, 1, 0, 0]]

# !!!假定匯入資料都為列向量，若行向量則需要對程式碼簡單修改

# 歐幾里德距離 這裡返回結果已處理 0，1   0最大相似，1最小相似   歐氏距離轉換為2範數計算
def ecludSim(inA,inB):
    return 1.0 / (1.0 + la.norm(inA-inB))

# 皮爾遜相關係數 numpy的corrcoef函式計算
def pearsSim(inA,inB):
    if(len(inA) < 3):
        return 1.0
    return 0.5 + 0.5*corrcoef(inA,inB,rowvar=0)[0][1]   # 使用0.5+0.5*x 將-1，1 轉為 0，1

# 餘玄相似度 根據公式帶入即可，其中分母為2範數計算，linalg的norm可計算範數
def cosSim(inA,inB):
    num = float(inA.T * inB)
    denom = la.norm(inA) * la.norm(inB)
    return 0.5 + 0.5*(num/denom)    # 同樣操作轉換 0，1


# 對物品評分  (資料集 使用者行號 計算誤差函式 推薦商品列號)
def standEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]   # 獲得特徵列數
    simTotal = 0.0; ratSimTotal = 0.0   # 兩個計算估計評分值變數初始化
    for j in range(n):
        userRating = dataMat[user,j]    #獲得此人對該物品的評分
        if userRating == 0: # 若此人未評價過該商品則不做下面處理
            continue
        overLap = nonzero(logical_and(dataMat[:,item].A>0,dataMat[:,j].A>0))[0]   # 獲得相比較的兩列同時都不為0的資料行號
        if len(overLap) == 0:
            similarity = 0
        else:
            # 求兩列的相似度
            similarity = simMeas(dataMat[overLap,item],dataMat[overLap,j])  # 利用上面求得的兩列同時不為0的行的列向量 計算距離
        # print('%d 和 %d 的相似度是: %f' % (item, j, similarity))
        simTotal += similarity  # 計算總的相似度
        ratSimTotal += similarity * userRating  # 不僅僅使用相似度，而是將評分當權值*相似度 = 貢獻度
    if simTotal == 0:   # 若該推薦物品與所有列都未比較則評分為0
        return 0
    else:
        return ratSimTotal/simTotal # 歸一化評分 使其處於0-5（評級）之間

# 給出推薦商品評分
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    unratedItems = nonzero(dataMat[user,:].A==0)[1]  # 找到該行所有為0的位置（即此使用者未評價的商品，才做推薦）
    if len(unratedItems) == 0:
        return '所有物品都已評價...'
    itemScores = []
    for item in unratedItems:   # 迴圈所有沒有評價的商品列下標
        estimatedScore = estMethod(dataMat, user, simMeas, item)    # 計算當前產品的評分
        itemScores.append((item, estimatedScore))
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]   # 將推薦商品排序

# 結果測試如下：
myMat = mat(loadExData())
myMat[0,1] = myMat[0,0] = myMat[1,0] = myMat[2,0] = 4   # 將資料某些值替換，增加效果
myMat[3,3] = 2
result1 = recommend(myMat,2)        # 餘玄相似度
print(result1)
result2 = recommend(myMat,2,simMeas=ecludSim)   # 歐氏距離
print(result2)
result3 = recommend(myMat,2,simMeas=pearsSim)   # 皮爾遜相關度
print(result3)

上面程式碼種用了三種計算距離的函式，經過測試後使用其中一種便可以了。然後對於物品評分函式中的nonzero(logical_and)不是很明白的請看這篇專門講解的文章。以上為普通的處理方式，下面使用SVD來做基於物品協同過濾。

SVD方法，用下面函式（svdEst）來替換上面的物品評價函式（standEst）即可，並且這裡使用更復雜的資料集：

# （使用者x商品）    # 為0表示該使用者未評價此商品，即可以作為推薦商品
def loadExData2():
    return [[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
            [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
            [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
            [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
            [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
            [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
            [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
            [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
            [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
            [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
            [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]

# 替代上面的standEst(功能) 該函式用SVD降維後的矩陣來計算評分
def svdEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    U,Sigma,VT = la.svd(dataMat)
    Sig4 = mat(eye(4)*Sigma[:4])  #將奇異值向量轉換為奇異值矩陣
    xformedItems = dataMat.T * U[:,:4] * Sig4.I  # 降維方法 通過U矩陣將物品轉換到低維空間中 （商品數行x選用奇異值列）
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j == item:
            continue
        # 這裡需要說明：由於降維後的矩陣與原矩陣代表資料不同（行由使用者變為了商品），所以在比較兩件商品時應當取【該行所有列】 再轉置為列向量傳參
        similarity = simMeas(xformedItems[item,:].T,xformedItems[j,:].T)
        # print('%d 和 %d 的相似度是: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0:
        return 0
    else:
        return ratSimTotal/simTotal

# 結果測試如下：
myMat = mat(loadExData2())
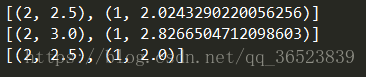
result1 = recommend(myMat,1,estMethod=svdEst)   # 需要傳參改變預設函式
print(result1)
result2 = recommend(myMat,1,estMethod=svdEst,simMeas=pearsSim)
print(result2)

上面的之所以使用4這個數字，是因為通過預先計算得到能滿足90%的奇異值能量的前N個奇異值。判斷計算如下：

# 選出奇異值能量大於90%的所有奇異值
myMat = mat(loadExData2())
U,sigma,VT = linalg.svd(myMat)
sigma = sigma**2    # 對奇異值求平方
cnt = sum(sigma)    # 所有奇異值的和
print(cnt)
value = cnt*0.9     # 90%奇異值能量
print(value)
cnt2 = sum(sigma[:3])   # 2小於90%，前3個則大於90%，所以這裡選擇前三個奇異值
print(cnt2)

# 541.9999999999995
# 487.7999999999996
# 500.5002891275793

在函式svdEst中使用SVD方法，將資料集對映到低緯度的空間中，再做運算。其中的xformedItems = dataMat.T*U[:,:4]*Sig4.I可能不是很好理解，它就是SVD的降維步驟，通過U矩陣和Sig4逆矩陣將商品轉換到低維空間（得到 商品行，選用奇異值列）。

以上是SVD的一個示例，但是對此有幾個問題：

  1. 我們不必在每次評分是都做SVD分解，大規模資料上可能降低效率，可以在程式呼叫時執行一次，在大型系統中每天執行一次或頻率不高，還要離線執行；
  2. 矩陣中有很多0，實際系統中0更多，可以通過只儲存非0元素來節省空間和計算開銷；
  3. 計算資源浪費來自於相似度的計算，每次一個推薦時都需要計算多個物品評分（即相似度），在需要時此記錄可以被使用者重複使用。實際中，一個普遍的做法是離線計算並儲存相似度得分，這一點在之前學習集體程式設計智慧中有說明。

基於SVD的影象壓縮：

這裡不採用書中的例子來講解，因為無趣所以這裡換作我們的男神來做一個簡單的SVD圖片壓縮作為一個示例：

首先放上男神圖片：

基於SVD圖片壓縮原理其實很簡單，圖片其實就是數字矩陣，通過SVD將該矩陣降維，只使用其中的重要特徵來表示該圖片從而達到了壓縮的目的。

直接上程式碼：

# 男神老吳SVD處理

from skimage import io
import matplotlib.pyplot as plt

path = 'male_god.jpg'
data = io.imread(path)
data = mat(data)        # 需要mat處理後才能在降維中使用矩陣的相乘
U,sigma,VT = linalg.svd(data)
# 在重構之前，依據前面的方法需要選擇達到某個能量度的奇異值
cnt = sum(sigma)
print(cnt)
cnt90 = 0.9*cnt    # 達到90%時的奇異總值
print(cnt90)
count = 50        # 選擇前50個奇異值
cntN = sum(sigma[:count])
print(cntN)

# 重構矩陣
dig = mat(eye(count)*sigma[:count]) # 獲得對角矩陣
# dim = data.T * U[:,:count] * dig.I # 降維 格外變數這裡沒有用
redata = U[:,:count] * dig * VT[:count,:]   # 重構

plt.imshow(redata,cmap='gray')  # 取灰
plt.show()  # 可以使用save函式來儲存圖片

原圖片為870x870，儲存畫素點值為870x870 = 756900，使用SVD，取前50個奇異值則變為：

(870+1+870)*50=87050

儲存量大大減小，僅50個奇異值就已經能很好的反應原資料了。

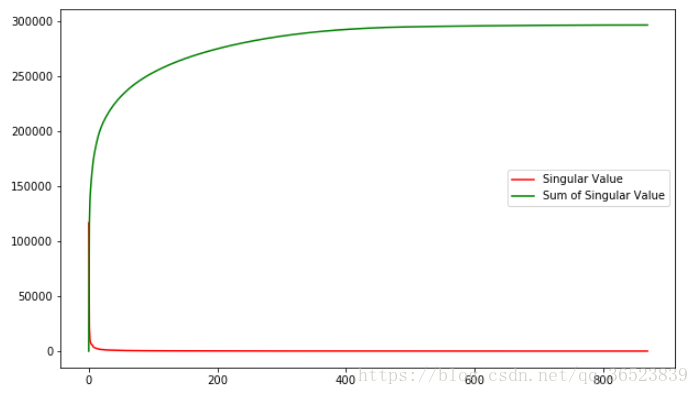
值得一提的是，奇異值從大到小衰減得特別快，在很多情況下，前 10% 甚至 1% 的奇異值的和就佔了全部的奇異值之和的 99% 以上了。這對於資料壓縮來說是個好事。下面這張圖展示了本例中奇異值和奇異值累加的分佈（參考部落格下面附上鍊接）：

SVD兩個個人覺得最重要的計算步驟這裡說一下：

  1. 資料集降維：newdata = data.T * U[:,:count] * sigma.I    這裡的sigma為對角矩陣（需要利用原來svd返回的sigma向量構建矩陣，構建需要使用count這個值）。U為svd返回的左奇異矩陣，count為我們指定的多少個奇異值，這也是sigma矩陣的維數。
  2. 重構資料集：redata = U[:,:count] * sigma * VT[:count,:]    這裡的sigma同樣為對角矩陣（需要利用原來svd返回的sigma向量構建矩陣，構建需要使用count這個值），VT為svd返回的右奇異矩陣，count為我們指定的多少個奇異值（可以按能量90%規則選取）。

以上為兩個個人覺得最重要的公式，如果有不明白的可以參考上面的程式碼，有使用到這兩個公式。（雖然不負責任，但還是說一下：如果你不能立刻理解SVD的原理，可以先記下這兩個公式來使用，後面有時間了在來深入瞭解哈哈）

參考書籍：《機器學習實戰》

相關推薦

機器學習實戰——SVD（奇異值分解）

與PCA一樣的學習過程，在學習SVD時同樣補習了很多的基礎知識，現在已經大致知道了PCA的應用原理，SVD個人感覺相對要難一點，但主要步驟還是能勉強理解，所以這裡將書本上的知識和個人的理解做一個記錄。主要關於（SVD原理、降維公式、重構原矩陣、SVD的兩個實際應用），當然矩陣

SVD（奇異值分解）小結

注：奇異值分解在資料降維中有較多的應用，這是把它的原理簡單總結一下，並個圖片壓縮的例子，最後做一個簡單的分析，希望能夠給大家帶來幫助。 1、特徵值分解（EVD） 實對稱矩陣 在理角奇異值分解之前，需要先回顧一下特徵值分解，如果矩陣\(A\)是一個\(m\times m\)的實對稱矩陣（即\(A

【機器學習筆記14】奇異值分解(SVD)

奇異值分解 定義: 假設A是一個m×nm \times nm×n的矩陣，則存在如下一種分解: Am×n=Um×m∑m×nVn×nTA_{m \times n}=U_{m \times m} \sum_{m \times n} V_{n \times n}^T

SVD分解（奇異值分解）求旋轉矩陣

參考文獻：http://igl.ethz.ch/projects/ARAP/svd_rot.pdf 一 問題描述 假設P={p1,p2,...,pn}和Q={q1,q2,...,qn}是兩組Rd空間中的對應點集，現在想要根據這個兩個點集的資料來計算出它們之間的剛性轉置

機器學習實戰——PCA（主成分分析）

本章關於PCA的程式碼雖少，但涉及到的知識卻很多，由於數學知識比較淺薄，所以在看這章時提前查詢資料複習了很多的概率論和統計學知識和python基礎知識，這裡記錄的很多都是關於PCA的相關知識或理論（例如：特徵向量、協方差矩陣等），由於部分知識涉及較多，講的有點詳細所以文章篇幅

PCA原理以及python實現（另外說說SVD奇異值分解）

說明：大部分內容摘自這個連結http://blog.codinglabs.org/articles/pca-tutorial.html，但是由於打不開了，，，也沒聯絡到博主，若侵權，望諒解，聯絡我刪除，我覺得原文寫得非常好所以分享到這裡，演算法實現部分以及第3點還有少點雜七雜

從矩陣（matrix）角度討論PCA（Principal Component Analysis 主成分分析）、SVD（Singular Value Decomposition 奇異值分解）相關原理

0. 引言 本文主要的目的在於討論PAC降維和SVD特徵提取原理，圍繞這一主題，在文章的開頭從涉及的相關矩陣原理切入，逐步深入討論，希望能夠學習這一領域問題的讀者朋友有幫助。 這裡推薦Mit的Gilbert Strang教授的線性代數課程，講的非常好，循循善誘，深入淺出。 Relevant Link:&

機器學習實戰筆記（python3實現）01--概述

apriori 一個 python 系列 k-均值聚類 思路 機器學習實戰 st算法 apr 寫在前面：這一個多月都在學習python,從python3基礎、python爬蟲、python數據挖掘與數據分析都有接觸，最近看到一本機器學習的書（主要是學習相關算法） 於是就打算

機器學習實戰一（kNN）

.com block 個數 indices 操作 來看 空間 計算機 python3 機器學習實戰一（kNN） 跟著老師做一個項目，關於行車記錄儀識別前方車輛，並判斷車距，不太好做。本來是用OpenCV，做著做著，突然發現需要補習一下機器學習的內容。《機器學習實戰（mach

機器學習實戰三（Naive Bayes）

需要 blog bag puts list tps foo 實戰 簡單的 機器學習實戰三（Naive Bayes） 前兩章的兩種分類算法，是確定的分類器，但是有時會產生一些錯誤的分類結果，這時可以要求分類器給出一個最優的猜測結果，估計概率。樸素貝葉斯就是其中一種。 學過概率

機器學習實戰教程（一）：線性回歸基礎篇（上）

學習 reg style spa 目標 pub auto 機器 輸入 一 什麽是回歸？ 　　回歸的目的是預測數值型的目標值，最直接的辦法是依據輸入，寫入一個目標值的計算公式。 　　假如你想預測小姐姐男友汽車的功率，可能會這麽計算： 　　　　　　　　　　　　　　Ho

機器學習實戰筆記（K近鄰）

最終 而是 類別 頻率 n) 簡單 因此 當前 要素 K近鄰算法（KNN） k近鄰算法 ??k近鄰(k-nearest neighbor,KNN)是一種基本的分類與回歸算法。於1968年由Cover和Hart提出。k近鄰的輸入是實例的特征向量，對應於特征空間的點；輸出為實

機器學習實戰SVD語法:

1.字典排序 from numpy import* from numpy import linalg as la A=[('a',2),('b',1),('c',5)] print(sorted(A, key=lambda jj : jj[1], reverse=True)) sorted(A,

機器學習實戰筆記（一）- 使用SciKit-Learn做回歸分析

err 皮爾遜 練習 using flow 相關 一個數 ocean 針對 一、簡介 這次學習的書籍主要是Hands-on Machine Learning with Scikit-Learn and TensorFlow（豆瓣：https://book.douban.co

《機器學習實戰》（一）knn演算法

K最近鄰（k-Nearest Neighbor，KNN）分類演算法可以說是最簡單的機器學習演算法了。它採用測量不同特徵值之間的距離方法進行分類。它的思想很簡單：存在一個樣本資料集合，也稱作訓練樣本集，並且樣本集中每個資料都存在標籤，即我們知道樣本集中每一個數據與所屬分類的對應關係。輸入沒有標

機器學習實戰教程（十二）：線性迴歸提高篇之樂高玩具套件二手價預測

一、前言 本篇文章講解線性迴歸的縮減方法，嶺迴歸以及逐步線性迴歸，同時熟悉sklearn的嶺迴歸使用方法，對樂高玩具套件的二手價格做出預測。 二、嶺迴歸 如果資料的特徵比樣本點還多應該怎麼辦？很顯然，此時我們不能再使用上文的方法進行計算了，因為矩陣X不是滿秩矩陣，非

機器學習實戰教程（三）：決策樹實戰篇之為自己配個隱形眼鏡

原文連結：cuijiahua.com/blog/2017/1… 一、前言 上篇文章機器學習實戰教程（二）：決策樹基礎篇之讓我們從相親說起講述了機器學習決策樹的原理，以及如何選擇最優特徵作為分類特徵。本篇文章將在此基礎上進行介紹。主要包括： 決策樹構建 決策樹視覺化 使用決

《機器學習實戰》（第二章）中函式詳細解析

本文是針對《機器學習實戰》內函式的解析。並以頁數呈現。 P19：numpy.tile(A,rep)函式 當rep為數字時，生成一個一維重複rep次的list。 當rep為元組（m,n）時，生成一個m行並且每行重複n次的矩陣。 import numpy as np a1

機器學習實戰——筆記（第一章）

機器學習基礎 目錄 機器學習的簡單概述 機器學習的主要任務 演算法選擇與開發步驟 Python語言的優勢 一、機器學習的簡單概述 機器學習應用領域十分廣泛，如人臉識別、推薦系統、手寫數字辨識及垃圾郵件過濾等。那何謂“機器學習”？ 簡單的說“

《機器學習實戰》（1）kNN小結（小白教學，每行程式碼都有註釋）

最近入坑了機器學習，為了快速提高自己的機器學習的程式碼能力，入坑了《機器學習實戰》，目前只學習了第一個重要演算法:k近鄰演算法（kNN），在學習過程中發現許多相關的學習資料要麼程式碼是python2的，要麼程式碼的解釋不夠詳細，對於像我這樣的菜雞而言苦不堪言，為了後來者不踩我