殘差分析(殘差原理與標準化殘差分析)
阿新 • • 發佈:2018-12-18
1、殘差分析定義
在迴歸模型 中,假定
的期望值為0,方差相等且服從正態分佈的一個隨機變數。但是,若關於
的假定不成立,此時所做的檢驗以及估計和預測也許站不住腳。確定有關
的假定是否成立的方法之一是進行殘差分析(residual analysis).
2、殘差與殘差圖
殘差(residual)是因變數的觀測值與根據估計的迴歸方程求出的預測
之差,用e表示。反映了用估計的迴歸方程去預測
而引起的誤差。第i個觀察值的殘差為:
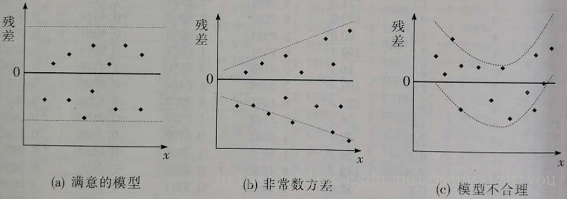
常用殘差圖:有關x殘差圖,有關的殘差圖,標準化殘差圖
有關x殘差圖:用橫軸表示自變數x的值,縱軸表示對應殘差 ,每個x的值與對應的殘差用圖上的一個點來表示。
分析殘差圖,首先考察殘差圖的形態及其反映的資訊。
分析:
(a)對所有x值,的方差都相同,且描述變數x和y之間的迴歸模型是合理的,殘差圖中的所有點落在一條水平帶中間。
(b)對所有的值,的方差是不同的,對於較大的x值,相應的殘差也較大,違背了
的方差相等的假設
(c)表明所選的迴歸模型不合理,應考慮曲線迴歸或多元迴歸模型。
3、標準化殘差
對於正態性假定的檢驗,也可通過標準化殘差分析完成。
標準化殘差(standardized residual)是殘差除以其標準差後得到的數值,也稱Pearson殘差或半學生化殘差(semi-studentized residuals),用表示。第i個觀察值的標準化殘差為:
(
是殘差的標準差的估計)
如果誤差項 服從正態分佈的這一假定成立,則標準化殘差的分佈也服從正態分佈。大約有95%的標準化殘差在 -2~2 之間。
從圖中可以看出,除了箭頭所標識的點外,所有的標準化殘差都在 -2~2 之間,所以誤差項服從正態分佈的假定成立。