模糊聚類分析
阿新 • • 發佈:2018-12-18
感覺 PPT 有點亂,這裡整理一下。
文章目錄
基於模糊等價矩陣的聚類分析方法
主要步驟有三個:
- 建立模糊矩陣
- 建立模糊等價矩陣
- 聚類(求動態聚類圖)
下面將分別介紹
建立模糊矩陣
設
為待分類的全體物件,其中每個待分類物件由一組資料表徵如下:
{
}
問題轉化為:如何建立物件
之間的相似關係,其中
建立模糊相似矩陣
建立模糊相似矩陣的注意事項:
- 自反
- 對稱
主要過程如下
資料預處理——資料標準化
設論域 U ={x1, x2, …, xn } 為待聚類物件,每個物件由 m 個指標表示其性狀:
{
}
將原始資料矩陣中的元素通過適當的變換壓縮到 [0, 1] 上。
有如下兩種常用的方法
平移-極差變換(變換至0-1區間)
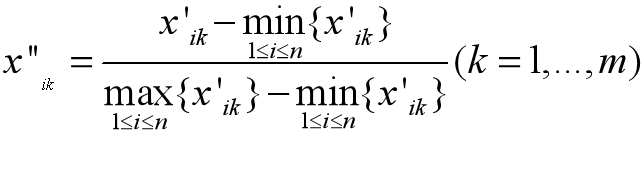
平移-標準差變換(消除量綱)
值得一提的是,這種方法不一定會把原始資料矩陣中的元素壓縮到 [0, 1] 上
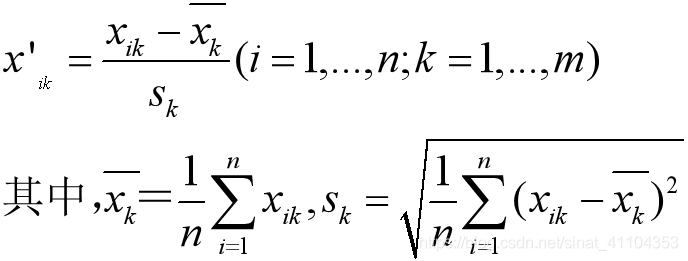
模糊相似矩陣的建立
相似係數法
數量積法
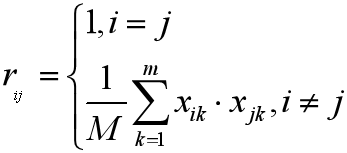
其中M為一適當選擇的正數,滿足
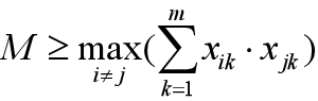
此時, ,若存在 ,令所有 使得
夾角餘弦法
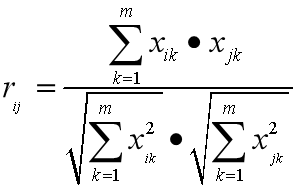
相關係數法
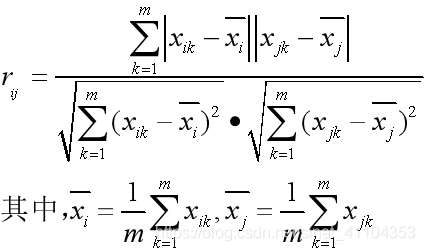
指數相似係數法
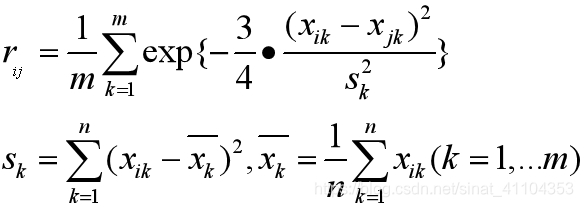 指數相似係數法中一行表示一個樣本的多個屬性。
指數相似係數法中一行表示一個樣本的多個屬性。
最大最小法
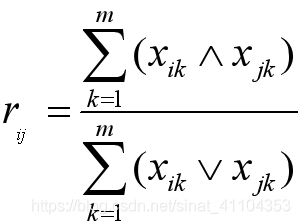
算數平均最小法
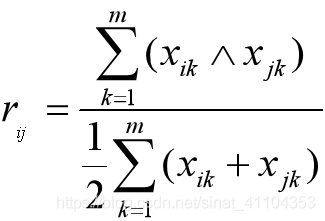
幾何平均最小法
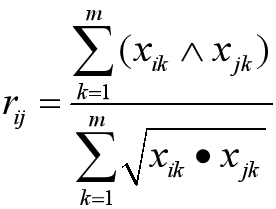
上述三種方法要求 xij>0,否則也要作適當變換。
距離法
絕對值倒數法
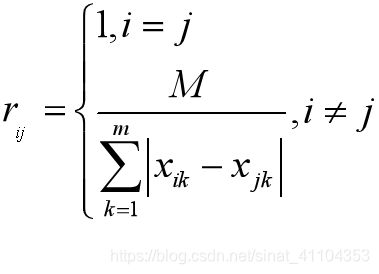
絕對值減數法
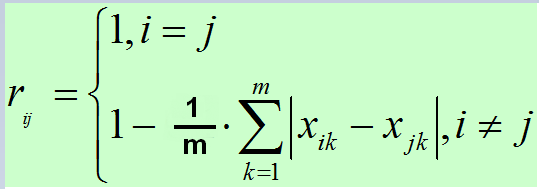
絕對值指數法
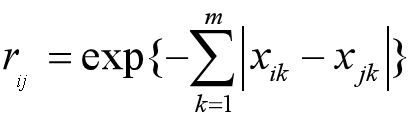
直接距離法
海明距離
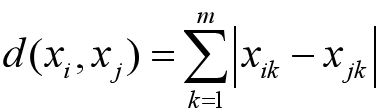
歐式距離
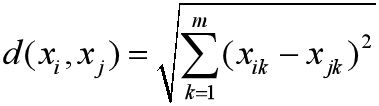
切比雪夫距離
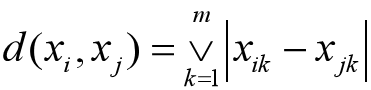
主觀評分法
專家直接給出相似度,專家數為 N,r_{ij}(k)表示第 k 個專家給出的 i 與 j 的相似度,
為專家的自信度。
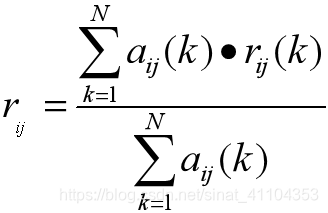
建立模糊等價矩陣
相似關係->等價關係
一般採用平方法來求傳遞閉包,也就是模糊等價矩陣
計算次數如下:
模糊相似矩陣 5×5
k = [log25]+1=2+1=3
最壞情況下,
聚類(求動態聚類圖)
對傳遞閉包依次取截關係
直接基於模糊相似矩陣聚類
建立模糊相似矩陣 R 後,求其傳遞閉包 t® 計算量較大。
若直接從 R 出發,進行聚類,會怎麼樣?
