折線分割平面（直線分割平面）

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 40736 Accepted Submission(s): 27006

Problem Description

我們看到過很多直線分割平面的題目，今天的這個題目稍微有些變化，我們要求的是n條折線分割平面的最大數目。比如，一條折線可以將平面分成兩部分，兩條折線最多可以將平面分成7部分，具體如下所示。

Input

輸入資料的第一行是一個整數C,表示測試例項的個數，然後是C 行資料，每行包含一個整數n(0<n<=10000),表示折線的數量。

Output

對於每個測試例項，請輸出平面的最大分割數，每個例項的輸出佔一行。

Sample Input

2
1
2

Sample Output

2
7

利用遞推思想先推導直線分割平面

通過拆分可得

n=1 ··· ··· 2=1+1；

n=2 ··· ··· 4=1+1+2；

n=3 ··· ··· 7=1+1+2+3;

n=4 ··· ··· 11=1+1+2+3+4;

n=5 ··· ··· 15=1+1+2+3+4+5;

··· ···

不難推出遞推n條直線分割平面公式S(n)
\[ S(n)=1+\sum_{i=1}^n \]
接下來我們再推折線分割平面公式

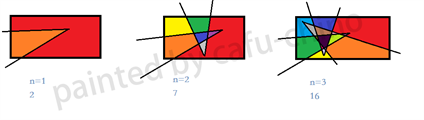
有上圖可知直線最大單獨分割4個平面而折線單獨分割2個，進一步歸納可得n條折線最大分割數等於2n條直線所分割數減去2n；即
\[ Z(n)=S(2n)-2n \]
由此就可以得出本題答案

程式碼樣例

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        int n;
        long long sum=0;
        cin >> n;
        for(int i=1; i <= 2*n; i++)
            sum+=i;
        cout << sum+1-2*n << endl;
    }
    return 0;
}