題目背景

NOIP2017提高組 DAY2 T3

題目描述

Sylvia 是一個熱愛學習的女孩子。 前段時間，Sylvia 參加了學校的軍訓。眾所周知，軍訓的時候需要站方陣。Sylvia 所在的方陣中有 n×m 名學生，方陣的行數為 n，列數為 m 。

為了便於管理，教官在訓練開始時，按照從前到後，從左到右的順序給方陣中的學生從 1 到 n×m 編上了號碼（參見後面的樣例）。即：初始時，第 i 行第 j 列的學生的編號是 (i-1)×m+j。

然而在練習方陣的時候，經常會有學生因為各種各樣的事情需要離隊。在一天中，一共發生了 q 件這樣的離隊事件。每一次離隊事件可以用數對 (x,y) （1≤x≤n,1≤y≤m）描述，表示第 x 行第 y 列的學生離隊。

在有學生離隊後，隊伍中出現了一個空位。為了隊伍的整齊，教官會依次下達這樣的兩條指令： 1. 向左看齊。這時第一列保持不動，所有學生向左填補空缺。不難發現在這條指令之後，空位在第 x 行第 m 列。 2. 向前看齊。這時第一行保持不動，所有學生向前填補空缺。不難發現在這條指令之後，空位在第 n 行第 m 列。

教官規定不能有兩個或更多學生同時離隊。即在前一個離隊的學生歸隊之後，下一個學生才能離隊。因此在每一個離隊的學生要歸隊時，隊伍中有且僅有第 n 行第 m  列一個空位，這時這個學生會自然地填補到這個位置。

因為站方陣真的很無聊，所以 Sylvia 想要計算每一次離隊事件中，離隊的同學的編號是多少。

注意：每一個同學的編號不會隨著離隊事件的發生而改變，在發生離隊事件後方陣中同學的編號可能是亂序的。

輸入格式

輸入共 q+1 行。 第 1 行包含 3 個用空格分隔的正整數 n，m，q，表示方陣大小是 n 行 m 列，一共發生了 q 次事件。 接下來 q 行按照事件發生順序描述了 q 件事件。每一行是兩個整數 x，y，用一個空格分隔，表示這個離隊事件中離隊的學生當時排在第 x 行第 y 列。

輸出格式

按照事件輸入的順序，每一個事件輸出一行一個整數，表示這個離隊事件中離隊學生的編號。

樣例資料 1

輸入

2 2 3 1 1 2 2 1 2

輸出

1 1 4

備註

【輸入輸出樣例1說明】

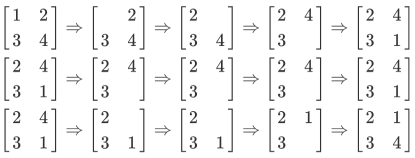
列隊的過程如上圖所示，每一行描述了一個事件。

在第一個事件中，編號為1的同學離隊，這時空位在第一行第一列。接著所有同學向左標齊，這時編號為 2 的同學向左移動一步，空位移動到第一行第二列。然後所有同學向上標齊，這時編號為 4 的同學向上一步，這時空位移動到第二行第二列。最後編號為 1 的同學返回填補到空位中。

【資料規模與約定】

資料保證每一個事件滿足 1≤x≤n；1≤y≤m。

解析：

       線段樹。

       實現前30分直接模擬。

       然後我們來看n=1的情況，只需要找出第K個數，將它移到隊尾即可，於是就可以愉快地 Treap/Splay 啦。

       因為M不大，於是考慮用權值線段樹，每次找出第K個沒有使用的位置。

       1.如果找到的數小等於M，將它標記為使用，加進 vector 中。

       2.如果找道的數大於M，則實際值即為 vector 裡的第 num-M 個數。

       對於100%的資料，我們仍可以使用以上做法，對每一行都建一顆權值線段樹。特別的，我們還要對最後一列建一顆權值線段樹。對於每個操作，分兩種情況：

       1.該位置 (x，y) 中若 y<m，則先修改第 x 行的線段樹，然後當加入 vector 時，我們不能直接加入這個數，因為由於最後一列要整體上移，所以，所以要先在最後一列的權值線段樹上查詢第 x 個位置（x，m）對應的數加入 vector ，然後再把這個刪除的數加入最後一列的線段樹的末尾。

       2.該位置 (x，y) 中若 y<=m，則直接在最後一列線段樹上查詢和修改。

       線段樹要動態開點，注意開 。

       分析一下時間與空間複雜度：

       首先時間複雜度容易知道是：

       其次空間複雜度，由於是動態開點，所以每次查詢Q次，每次更新 logN 個節點，所以大致還是

程式碼：

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int Max=300005;
int n,m,q,sum,tot;
int tree[Max*20],lc[Max*20],rc[Max*20],rt[Max];
vector<int>num[Max];

inline int get_int()
{
	int x=0;char c;
	for(c=getchar();!isdigit(c);c=getchar());
	for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+c-'0';
	return x;
}
inline void print(int x)
{
	if(x>9) print(x/10);
	putchar('0'+x%10);
}

inline void add(int &now,int l,int r,int pos)  //更新 
{
	if(!now) now=++tot;tree[now]++;
	if(l==r) return;
	int mid=(l+r)>>1;
	if(pos<=mid) add(lc[now],l,mid,pos);
	else add(rc[now],mid+1,r,pos);
}
inline int Q(int root,int l,int r,int k)     //查詢 
{
	if(l==r) return l;
	int mid=(l+r)>>1,sum=(mid-l+1)-tree[lc[root]];
	if(sum>=k) Q(lc[root],l,mid,k);
	else Q(rc[root],mid+1,r,k-sum);
}
inline int Qr(int x,int v)      //最後一列 
{
	int pos=Q(rt[n+1],1,sum,x);add(rt[n+1],1,sum,pos);
	int ans=pos<=n?m*pos:num[n+1][pos-n-1];
	num[n+1].push_back(v?v:ans);
	return ans;
}
inline int Ql(int x,int y)     //1~m-1列 
{
	int pos=Q(rt[x],1,sum,y);add(rt[x],1,sum,pos);
	int ans=pos<m?(x-1)*m+pos:num[x][pos-m];
	num[x].push_back(Qr(x,ans)); 
	return ans;
}

signed main()
{
	n=get_int(),m=get_int(),q=get_int(),sum=max(n,m)+q;
	while(q--)
	{
	  int x=get_int(),y=get_int();
	  if(y==m) print(Qr(x,0)),putchar('\n');
	  else print(Ql(x,y)),putchar('\n');
	}
	return 0;
}