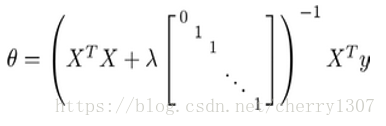機器學習練習2——正則化的Logistic迴歸

過擬合

	如果我們有非常多的特徵，我們通過學習得到的假設可能能夠非常好地適應訓練集（代價函式可能幾乎為0），但是可能會不能推廣到新的資料。
解決：
	1.丟棄一些不能幫助我們正確預測的特徵。可以是手工選擇保留哪些特徵，或者使用一些模型選擇的演算法來幫忙（例如PCA）
	2.正則化。 保留所有的特徵，但是減少引數的大小（magnitude）。

正則化

正則化(regularization)的技術，它可以改善或者減少過度擬合問題

線性迴歸

梯度下降

theta(0)不參與懲罰項

正規方法

Logistic迴歸

theta(0)不參與懲罰項

練習2

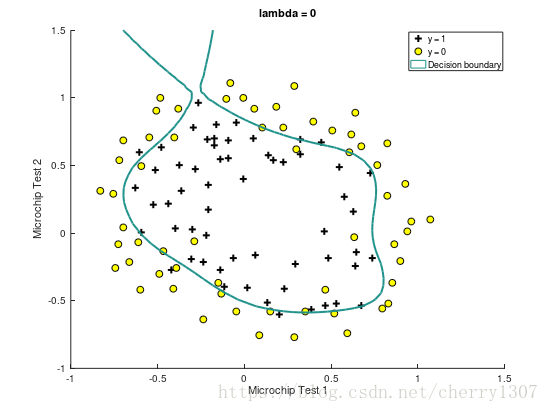
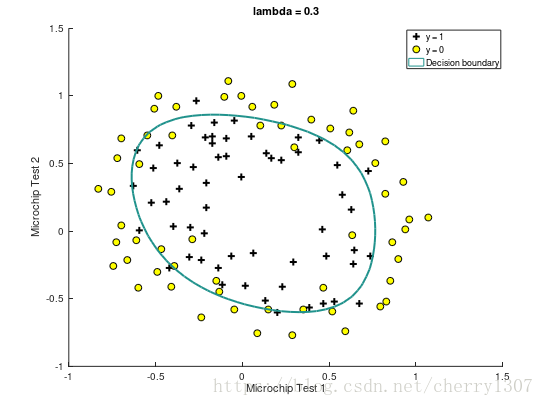
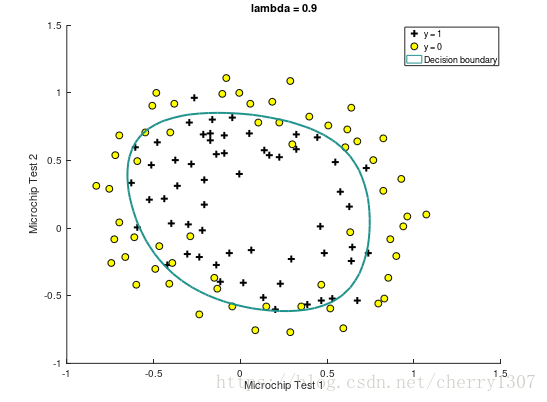
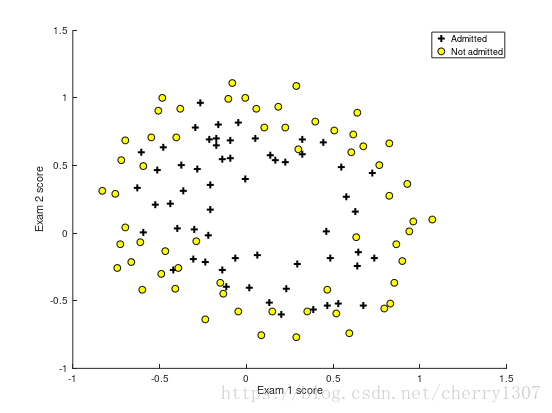
x1,x2 : the test results for some microchips on two dierent tests 
y : decision

視覺化資料集

特徵對映

function out = mapFeature(X1, X2)
degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end
end

特徵向量X的維度為：m*28

代價函式和梯度下降

function [J, grad] = costFunctionReg(theta, X, y, lambda)
	m = length(y); 
	J = 0;
	grad = zeros(size(theta));
	h = sigmoid(X*theta);
	J = (1/m)*sum((-y)'*log(h)-(1-y)'*log(1-h)) + lambda/(2*m)*sum(theta(2:end).^2);
	grad(1) = (1/m)*sum((h-y).*X(:,1));
for j = 2:size(X,2)
	grad(j) = (1/m)*sum((h-y).*X(:,j)) + lambda*theta(j)/m;	
end
 

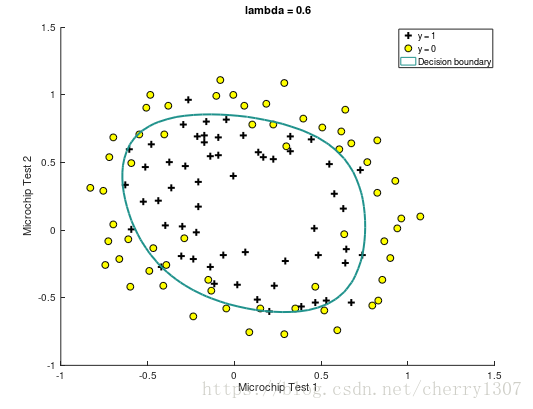
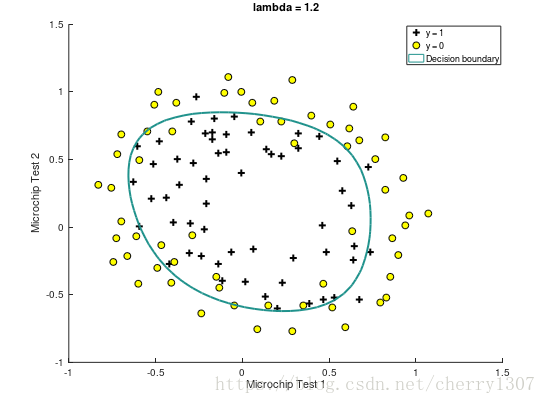
繪製出決策邊界