對誤差的最大似然估計
今天看了線性迴歸的視訊，在看到對誤差求似然估計函式的時候感覺很不解：
為啥對誤差的似然函式越大越好？
Picture1:真實值y
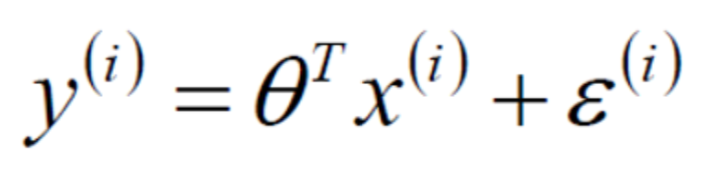Picture2:誤差ε服從高斯分佈：
誤差ε是獨立並且具有相同的分佈，並且服從均值為0方差為σ²的高斯分佈
如圖：Picture3:
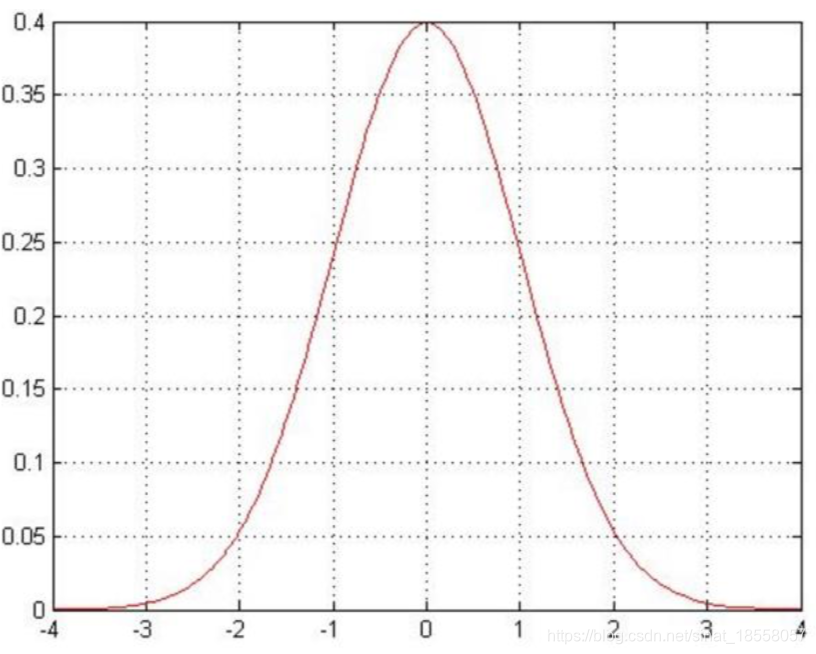當ε取0附近的時候p(ε)值最大。可知ε->0,ε的取值處於0的附近；那麼也就是說p(ε)的值要越大越好。從而似然函式越大越好。
相關推薦
對誤差的最大似然估計
今天看了線性迴歸的視訊，在看到對誤差求似然估計函式的時候感覺很不解： 為啥對誤差的似然函式越大越好？ Picture1:真實值y Picture2:誤差ε服從高斯分佈： 誤差ε是獨立並且具有相同的分佈，並且服從均值為0方差為σ²的高斯分佈 如圖：Pictur
【MLE】最大似然估計Maximum Likelihood Estimation
like 分布 什麽 9.png 顏色 ... 部分 多少 ati 模型已定，參數未知 最大似然估計提供了一種給定觀察數據來評估模型參數的方法，假設我們要統計全國人口的身高，首先假設這個身高服從服從正態分布，但是該分布的均值與方差未知。我們沒有人力與物力去統計
『科學計算_理論』最大似然估計
width 我們 註意 logs 概率 -s 分享 pan 技術 概述 通俗來講，最大似然估計，就是利用已知的樣本結果，反推最有可能（最大概率）導致這樣結果的參數值。 重要的假設是所有采樣滿足獨立同分布。 求解模型參數過程 假如我們有一組連續變量的采樣值（x1,x2,…,x
最小二乘法和最大似然估計的聯系和區別（轉）
enc bsp 聯系 角度 tro span nbsp sdn .science 對於最小二乘法，當從模型總體隨機抽取n組樣本觀測值後，最合理的參數估計量應該使得模型能最好地擬合樣本數據，也就是估計值和觀測值之差的平方和最小。而對於最大似然法，當從模型總體隨機抽取n組樣本觀
最大似然估計與最小二乘
現在 最小 bayesian 我不知道 什麽 改變 我不 tps 有關 參考： 最大似然估計，就是利用已知的樣本結果，反推最有可能（最大概率）導致這樣結果的參數值。例如：一個麻袋裏有白球與黑球，但是我不知道它們之間的比例，那我就有放回的抽取10次，結果我發現我抽到了8次黑球
最大似然估計
概率與統計 lin 是什麽 簡單的 art 不規則 導數 單調性 人類 在討論最大似然估計之前，我們先來解決這樣一個問題：有一枚不規則的硬幣，要計算出它正面朝上的概率。為此，我們做了 10 次實驗，得到這樣的結果：[1, 0, 1, 0, 0, 0, 0, 0, 0, 1]
最大似然估計實例 | Fitting a Model by Maximum Likelihood (MLE)
-- sed clu ans fail warnings reg model perf 參考：Fitting a Model by Maximum Likelihood 最大似然估計是用於估計模型參數的，首先我們必須選定一個模型，然後比對有給定的數據集，然後構建一個聯合概
【機器學習基本理論】詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解
總結 ora 二次 判斷 天都 特性 以及 解釋 意思 【機器學習基本理論】詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解 https://mp.csdn.net/postedit/81664644 最大似然估計（Maximum lik
最大似然估計（轉載）
轉載請註明出處，文章來源：https://blog.csdn.net/qq_36396104/article/details/78171600#commentsedit 之前看書上的一直不理解到底什麼是似然，最後還是查了好幾篇文章後才明白，現在我來總結一下吧，要想看懂最大似然估計，首
最大似然估計 最大似然估計 （MLE） 最大後驗概率（MAP）
最大似然估計 （MLE） 最大後驗概率（MAP） 1） 最大似然估計 MLE 給定一堆資料，假如我們知道它是從某一種分佈中隨機取出來的，可是我們並不知道這個分佈具體的參，即“模型已定，引數未知”。例如，我們知道這個分佈是正態分佈，但是不知道均值和方差；或者是二項分佈，但是不知道均值。 最
似然函式和最大似然估計與機器學習中的交叉熵函式之間的關係
關於似然函式和最大似然估計的詳細說明可以看這篇文章：https://blog.csdn.net/zgcr654321/article/details/83382729 二分類情況和多分類情況下的似然函式與最大似然估計： 二分類情況下的似然函式與最大似然估計： 我們知道按照生活中的常識
最大似然估計vs最大後驗概率
1） 最大似然估計 MLE 給定一堆資料，假如我們知道它是從某一種分佈中隨機取出來的，可是我們並不知道這個分佈具體的參，即“模型已定，引數未知”。例如，我們知道這個分佈是正態分佈，但是不知道均值和方差；或者是二項分佈，但是不知道均值。 最大似然估計（MLE，Maximum Lik
【模式識別與機器學習】——最大似然估計 （MLE） 最大後驗概率（MAP）
1） 極/最大似然估計 MLE 給定一堆資料，假如我們知道它是從某一種分佈中隨機取出來的，可是我們並不知道這個分佈具體的參，即“模型已定，引數未知”。例如，我們知道這個分佈是正態分佈，但是不知道均值和方差；或者是二項分佈，但是不知道均值。 最大似然估計（MLE，Maximum Likelihood Esti
最大似然估計的學習
首先聊聊題外話，很久沒有寫部落格了，一直喜歡用本子來記錄學習過程，但是這樣會有一個很大的弊端，就是本子儲存不了多久，最後還是選擇以部落格的方式來記錄所學的東西。這樣複習起來都會方便一些。我現在是一名在校生，以後學習的新東西儘量都會記錄下來，有相同經歷的朋友可以關注一下，一起交流。 最大似
人工智慧初學- 1.2 最大似然估計及貝葉斯演算法
最大似然思想 最大似然法是一種具有理論性的引數估計方法。 基本思想是：當從模型總體隨機抽取n組樣本觀測值後，最合理的引數估計量應該使得從模型中抽取該n組樣本觀測值的概率最大。一般步驟包括： 寫出似然函式 對似然
伯努利分佈和高斯分佈下的最大似然估計
最大似然估計： 由於每一個樣本是否出現都對應著一定的概率，而且一般來說這些樣本的出現都不那麼偶然，因此我們希望這個概率分佈的引數能夠以最高的概率產生這些樣本。如果觀察到的資料為D1 , D2 , D3 ，…， DN ，那麼極大似然的目標如下： 通常上面這個概率的計算並不容易。
詳解最大似然估計（MLE）、最大後驗概率估計（MAP），以及貝葉斯公式的理解
<svg xmlns="http://www.w3.org/2000/svg" style="display: none;"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id=
最大似然估計（MLE）、最大後驗概率估計（MAP）以及貝葉斯學派和頻率學派
前言 frequentist statistics：模型引數是未知的定值，觀測是隨機變數；思想是觀測數量趨近於無窮大+真實分佈屬於模型族中->引數的點估計趨近真實值；代表是極大似然估計MLE；不依賴先驗。 Bayesian statistics：模型引數是隨機變數，
機器學習概念：最大後驗概率估計與最大似然估計 （Maximum posterior probability and maximum likelihood estimation)
joey 周琦 假設有引數 θ \theta, 觀測 x \mathbf{x}, 設 f(x|θ) f(x|\theta)是變數 x x的取樣分佈， θ \th
最大似然估計和最大後驗概率估計（貝葉斯引數估計）
舉個例子：偷盜的故事，三個村莊，五個人偷。 村子被不同小偷偷的概率：P(村子|小偷1)、P(村子|小偷2)、P(村子|小偷3) 小偷1的能力：P(偷盜能力)=P(村子1|小偷1)+P(村子2|小偷1)+P(村子3|小偷1)+P(村子4|小偷1)+P(村子5|小偷1) 小