最大似然估計的學習
阿新 • • 發佈：2018-11-29
首先聊聊題外話，很久沒有寫部落格了，一直喜歡用本子來記錄學習過程，但是這樣會有一個很大的弊端，就是本子儲存不了多久，最後還是選擇以部落格的方式來記錄所學的東西。這樣複習起來都會方便一些。我現在是一名在校生，以後學習的新東西儘量都會記錄下來，有相同經歷的朋友可以關注一下，一起交流。
最大似然估計
最大似然估計是在已知樣本分佈，且已知資料的分佈模型，只是不知道模型的具體引數的情況下，用來估計引數的一種方法。方法的目的是尋找這樣一組引數，能使得在這些引數下產生已知樣本點的概率是最大的。
下面先舉一個通俗的例子，再舉一個具體的例項來說明這個問題（這樣我以後看起來也會容易懂一點）。
兩個人玩擲骰子游戲，一共玩了十把，每一把都是甲贏，贏就算了，他每次擲的骰子都是兩個6，然後乙就輸了很多錢，當乙的朋友知道這件事後就說，甲肯定輸出老千了。這樣的小故事我們生活中會遇到吧，那麼這個例子與最大似然估計有什麼關係呢？其實乙的朋友根據甲乙雙方進行的十局遊戲來判定甲出老千，就是一種最大似然估計估計的思想。
在公平的條件下，出現這種結局的概率是(1/36)^10。
在不公平的條件下，出現這種結局的概率就要大的多了。（80%或90%等）
根據結局推算出甲出老千，這就是一種最大似然的思維。
具體的例子
現在有一組樣本（x1,x2,…xn）,已知樣本滿足正態分佈N，引數為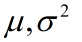
則出現系列樣本的概率可以寫成為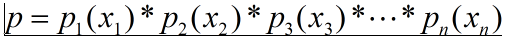
在這裡將這個概率寫為似然函式，記為：
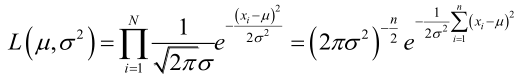
最大似然的目的在這裡就要體現出來了，就是要求一組引數
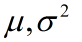使得似然函式最大（也就是在這組引數下出現這些樣本的概率最大），下面就是求最大值點的問題了。求導：
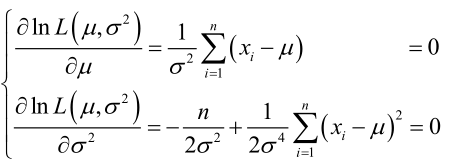
解得：
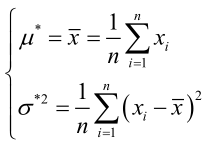
總結
以上是最大似然的淺層理解，總結一下求最大似然估計量的一般步驟：
- 寫似然函式
- 對似然函式取對數（乘積形式不好求導）
- 求導數
- 解方程
PS：我們此處討論的是概率模型是已知 的，但是在實際情況中，這種概率模型是不知道的，需要我們根據樣本的特徵的假設，假設概率模型很重要，估計的不好將對結果產生很大偏差。