KNN實現圖片的分類(python)
一 . K-近鄰演算法(KNN)概述
最簡單最初級的分類器是將全部的訓練資料所對應的類別都記錄下來,當測試物件的屬性和某個訓練物件的屬性完全匹配時,便可以對其進行分類。但是怎麼可能所有測試物件都會找到與之完全匹配的訓練物件呢,其次就是存在一個測試物件同時與多個訓練物件匹配,導致一個訓練物件被分到了多個類的問題,基於這些問題呢,就產生了KNN。
KNN是通過測量不同特徵值之間的距離進行分類。它的思路是:如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別,其中K通常是不大於20的整數。KNN演算法中,所選擇的鄰居都是已經正確分類的物件。該方法在定類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分樣本所屬的類別。
下面通過一個簡單的例子說明一下:如下圖,綠色圓要被決定賦予哪個類,是紅色三角形還是藍色四方形?如果K=3,由於紅色三角形所佔比例為2/3,綠色圓將被賦予紅色三角形那個類,如果K=5,由於藍色四方形比例為3/5,因此綠色圓被賦予藍色四方形類。
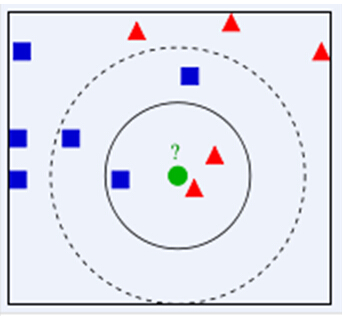
由此也說明了KNN演算法的結果很大程度取決於K的選擇。
在KNN中,通過計算物件間距離來作為各個物件之間的非相似性指標,避免了物件之間的匹配問題,在這裡距離一般使用曼哈頓距離(L1)或歐氏距離(L2):

同時,KNN通過依據k個物件中佔優的類別進行決策,而不是單一的物件類別決策。這兩點就是KNN演算法的優勢。
接下來對KNN演算法的思想總結一下:就是在訓練集中資料和標籤已知的情況下,輸入測試資料,將測試資料的特徵與訓練集中對應的特徵進行相互比較,找到訓練集中與之最為相似的前K個數據,則該測試資料對應的類別就是K個數據中出現次數最多的那個分類,其演算法的描述為:
1)計算測試資料與各個訓練資料之間的距離;
2)按照距離的遞增關係進行排序;
3)選取距離最小的K個點;
4)確定前K個點所在類別的出現頻率;
5)返回前K個點中出現頻率最高的類別作為測試資料的預測分類。
