最小生成樹演算法-Prim演算法
阿新 • • 發佈:2018-12-19
- 從任意一個頂點開始構造生成樹,假設從0號頂點開始。首先將頂點0加入到生成樹中,用一個一維陣列book標記哪些頂點已經加入到生成樹。
- 用一個數組dis記錄生成樹到各個頂點的距離。最初生成樹中只有0號頂點,當其餘頂點與0號頂點有直連邊時,陣列dis中儲存的就是0號頂點到該頂點的邊的權值。與0號頂點沒有直連邊的頂點對應的dis陣列中的元素設為無窮大。完成dis陣列初始化。
- 從陣列dis中選出離生成樹最近的頂點(假設這個頂點為j)加入到生成樹中(即在陣列dis中找未加入生成樹的點對應的dis元素最小值)。再以j為中間點,更新生成樹到每一個非樹頂點的距離(即鬆弛),即如果dis[k]>e[j][k] 則更新dis[k]=e[j][k]。(二維陣列e儲存的是圖中各個邊的資訊)。
- 重複第3步,直到生成樹中有n個頂點為止。
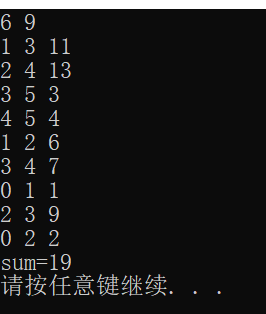
#include <iostream> #include <vector> using namespace std; #define inf 99999 int main() { int n, m; cin >> n >> m;//讀入n和m,n表示頂點個數,m表示邊的條數 vector<vector<int>> e(n, vector<int>(n, inf));//儲存圖中個頂點間的距離資訊 vector<bool> book(n,false); vector<int> dis(n); int count = 0, sum = 0;//count用來記錄生成樹中的頂點個數,sum用來儲存路徑之和 for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (i == j) { e[i][j] = 0; } } } //讀入邊 for (int i = 0; i < m; i++) { int t1, t2, t3; cin >> t1 >> t2 >> t3; e[t1][t2] = t3; //注意這裡是無向圖,所以需要將邊反向再儲存一遍 e[t2][t1] = t3; } //初始化dis陣列,當前生成樹中只有0號頂點,故儲存的是0號頂點到各個頂點的距離 for (int i = 0; i < n; i++) { dis[i] = e[0][i]; } //Prim演算法核心部分 //將0號頂點加入生成樹 book[0] = true; count++; while (count < n) { int min = inf; int j; for (int i = 0; i < n; i++) { if (book[i] == false && dis[i] < min) { min = dis[i]; j = i; } } book[j] = true; count++; sum += dis[j]; //掃描當前頂點j所有的邊,更新生成樹到每一個非樹頂點的距離 for (int i = 0; i < n; i++) { if (book[i] == false && dis[i] > e[j][i]) { dis[i] = e[j][i]; } } } cout << "sum=" << sum << endl; system("pause"); }
這種方法的時間複雜度為O(N^2),如果藉助“堆”,每次選邊的時間複雜度是O(logM),然後使用鄰接表來儲存圖的話,整個演算法的時間複雜度會降低到O(MlogN)。
使用堆來優化,我們需要3個數組。陣列dis用來記錄生成樹到各個頂點的距離。陣列h是一個最小堆,堆裡面儲存的是頂點編號。注意這裡不是按照頂點編號的大小來建立最小堆的,而是按照頂點在陣列dis中所對應的值來建立這個最小堆。此外還需要一個pos陣列來記錄每個頂點在最小堆h中的位置。
程式碼如下:
#include "pch.h" #include <iostream> #include <vector> using namespace std; #define inf 99999 //交換堆中兩個元素的值 void myswap(int x, int y, vector<int> &h, vector<int> &pos) { int temp; temp = h[x]; h[x] = h[y]; h[y] = temp; //同步更新pos陣列,pos陣列記錄的是每個頂點在堆中的位置 temp = pos[h[x]]; pos[h[x]] = pos[h[y]]; pos[h[y]] = temp; return; } //最小堆向下調整函式 i是需要向下調整的節點編號 h是最小堆的底層實現 void siftdown(int i, vector<int> &h, const int &size,vector<int> &dis, vector<int> &pos ) { bool flag = false; //flag用來標記是否需要繼續向下調整 int temp; while ((i + 1) * 2 - 1 < size && flag == false) { //比較i和它的左兒子(i+1)*2在dis中的值,並用temp記錄較小的節點編號 if (dis[h[(i + 1) * 2 - 1]] < dis[h[i]]) { temp = (i + 1) * 2 - 1; } else { temp = i; } //如果i有右兒子,則繼續比較 if ((i + 1) * 2 < size) { if (dis[h[(i + 1) * 2]] < dis[h[temp]]) { temp = (i + 1) * 2; } } if (temp != i) { myswap(temp, i, h, pos); i = temp;//更新i為剛與它交換的兒子節點的編號,便於接下來繼續向下調整 } else { flag = true; } } return; } void siftup(int i, vector<int> &h, const int &size, vector<int> &dis, vector<int> &pos) { bool flag = false; //用來標記是否需要向上調整 if (i == 0) { return; //如果是堆頂,就直接返回,不需要向上調整了 } //不在堆頂,並且i的值比父節點小的時候繼續向上調整 while (i != 0 && flag == false) { if (dis[h[i]] < dis[h[(i - 1) / 2]]) { myswap(i, (i - 1) / 2, h, pos); } else { flag = true; } i = (i - 1) / 2; } return; } int pop(vector<int> &h, int &size, vector<int> &dis, vector<int> &pos) { int t = h[0]; //用一個臨時變數記錄堆頂點的編號 pos[t] = -1;//彈出堆頂後,這個頂點已不在堆中了,故將該頂點對應的pos陣列中的值做相應處理 h[0] = h[size - 1];//將堆的最後一個點賦值到堆頂 pos[h[0]] = 0; size--; siftdown(0,h,size,dis,pos); return t; } int main() { int n, m; cin >> n >> m;//讀入n和m,n表示頂點個數,m表示邊的條數 vector<int> dis(n, inf);//記錄生成樹到各個頂點的距離 vector<bool> book(n, false);//記錄那些頂點已經在生成樹中了,true表示已經在生成樹中了 vector<int> h(n), pos(n);//h用來儲存最小堆,pos用來儲存各個頂點在最小堆中的位置 int size;//size為最小堆的大小 //u陣列儲存邊的起點,v陣列儲存邊的終點,w陣列儲存邊的權值 //first[i]表示以點i為起點的第一條邊的編號 //next[i]表示編號為i的邊的下一條邊的編號 //因為儲存的是無向圖,所以u、v、w、next陣列的大小是邊的條數的兩倍 vector<int> u(2*m), v(2*m), w(2*m),first(n,-1),next(2*m); //count儲存當前生成樹中頂點的個數,sum儲存當前路徑之和 int count = 0, sum = 0; //開始讀入邊 for (int i = 0; i < m; i++) { cin >> u[i] >> v[i] >> w[i]; } //由於是無向圖,故需把所有的邊再反向儲存一次 for (int i = m; i < 2 * m; i++) { u[i] = v[i - m]; v[i] = u[i - m]; w[i] = w[i - m]; } //初始化鄰接表 for (int i = 0; i < 2 * m; i++) { next[i] = first[u[i]]; first[u[i]] = i; } //Prim演算法核心部分開始 //將0號頂點加入生成樹 book[0] = true; count++; //初始化dis陣列為0號頂點到其餘各個頂點的初始距離 dis[0] = 0; int k = first[0]; while (k != -1) { dis[v[k]] = w[k]; k = next[k]; } //初始化最小堆 size = n; for (int i = 0; i < size; i++) { h[i] = i; pos[i] = i; } //因為堆中編號從0開始,所以i=size/2-1;如果是從1開始編號,那麼就是i=size/2; //只需要從倒數第二層從右向左第一個非葉節點開始向下調整即可 for (int i = size / 2 - 1; i >= 0; i--) { siftdown(i, h, size, dis, pos); } pop(h,size,dis,pos);//從堆頂彈出一個元素,因為此時堆頂是0號頂點 while (count < n) { int j = pop(h, size, dis, pos); book[j] = true; count++; sum += dis[j]; //掃描當前頂點j的所有邊,進行鬆弛 int k = first[j];//以j為起點的第一條邊的編號 while (k != -1) { if (book[v[k]] == false && dis[v[k]] > w[k]) { dis[v[k]] = w[k]; siftup(pos[v[k]],h,size,dis,pos);//對該點在堆中向上調整,因為該點對應的dis值變小了,所以只可能是向堆頂調整 } k = next[k]; } } cout << "sum=" << sum; system("pause"); }
如果所有的邊權都不相等,那麼最小生成樹是唯一的。
沒有使用堆優化的Prim演算法適用於稠密圖,使用了堆優化的Prim演算法則更適用於稀疏圖。
