矩陣特徵值、特徵向量及其求解

阿新 • • 發佈：2018-12-19

如果把矩陣看成運動，描述運動最重要的引數當屬運動的速度和方向。為了幫助大家理解，我們可以形象地認為：特徵值就是運動的速度，特徵向量就是運動的方向。

Python程式碼：

import numpy as np
w, v = np.linalg.eig(np.array([[1, -2], [2, -3]]))
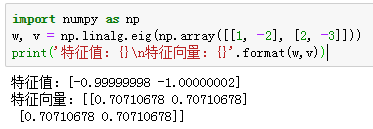
print('特徵值：{}\n特徵向量：{}'.format(w,v))

結果：

矩陣特徵值、特徵向量及其求解

如果把矩陣看成運動，描述運動最重要的引數當屬運動的速度和方向。為了幫助大家理解，我們可以形象地認為：特徵值就是運動的速度，特徵向量就是運動的方向。如果把矩陣看成運動，描述運動最重要的引數當屬運動的速

矩陣的特徵值、特徵向量及其程式碼求解實現

如果把矩陣看成運動，描述運動最重要的引數當屬運動的速度和方向。為了幫助大家理解，我們可以形象地認為：特徵值就是運動的速度，特徵向量就是運動的方向。 Python程式碼： import numpy as np w, v = np.linalg.eig(np.array([[1,

影象演算法的基礎知識(雙線性插值，協方差矩陣，矩陣的特徵值、特徵向量）

0. 前言 MATLAB或者OpenCV裡有很多封裝好的函式，我們可以使用一行程式碼直接呼叫並得到處理結果。然而當問到具體是怎麼實現的時候，卻總是一臉懵逼，答不上來。前兩天參加一個演算法工程師的筆試題，其中就考到了這幾點，感到非常汗顏！趕緊補習！ 1. 雙線性插值在影象處

矩陣特徵分解介紹及雅克比(Jacobi)方法實現特徵值和特徵向量的求解(C++/OpenCV/Eigen)

對角矩陣(diagonal matrix)：只在主對角線上含有非零元素，其它位置都是零，對角線上的元素可以為0或其它值。形式上，矩陣D是對角矩陣，當且僅當對於所有的i≠j, Di,j= 0. 單位矩陣就是對角矩陣，對角元素全部是1。我們用diag(v)表示一個對角元素由向量v

機器學習之線性代數基礎一矩陣乘法、秩、特徵值、特徵向量的幾何意義

寫篇文章把自己對矩陣的理解記錄一下，有不對的地方歡迎指正。為簡單、直觀、視覺化起見，我們只以簡單的二維和三維空間為例。高維空間也是同樣的道理，只是不能視覺化，只能通過數學公式來證明。 1. 矩陣乘法矩陣乘法來源於線性方程組的求解，為了方便起見，

[matlab] eig函式求解矩陣特徵值和特徵向量

在MATLAB中，計算矩陣A的特徵值和特徵向量的函式是eig(A)，常用的呼叫格式有 5種： (1) E=eig(A)：求矩陣A的全部特徵值，構成向量E。 (2) [V,D]=eig(A)：求矩陣A的全部特徵值，構成對角陣D，並求A的特徵向量構成 V的列

線性代數---矩陣---特徵值和特徵向量

轉自：https://jingyan.baidu.com/article/27fa7326afb4c146f8271ff3.html 一、特徵值和特徵向量的定義首先讓我們來了解一下特徵值和特徵向量的定義，如下：特徵子空間基本定義，如下：

C++ Eigen庫計算矩陣特徵值及特徵向量

C++Eigen庫程式碼 #include <iostream> #include <Eigen/Dense> #include <Eigen/Eigenvalues> using namespace Eigen

矩陣特徵值和特徵向量

介紹特徵向量和特徵值在計算機視覺和機器學習中有許多重要的應用。眾所周知的例子是PCA（主成分分析）進行降維或人臉識別是特徵臉。特徵向量和特徵值的一個有趣應用在我的另一篇有關誤差橢圓的博文中提到。此外，特徵值分解形成協方差矩陣幾何解釋的基礎。在這篇文章中，我將簡單的介紹這個數

c語言實現求一個矩陣特徵值和特徵向量

前言求矩陣的特徵值，主要是用的QR分解，在我的有一次部落格裡，我已經詳細地給出了計算的過程，大家有興趣可以去看下，經過幾天的鑽研，終於完成了整個的eig演算法。下面我將把我的整個程式碼附上，有不懂的可以問我，歡迎一起討論學習！這是對上一次

Jacobi迭代求矩陣特徵值和特徵向量+C程式碼

Jacobi計算過程如下： 1. 選擇矩陣A非對角元中最大值A[i][j]，運用公式 tan 2O = 2*A[i][j] / (A[i][i] -A[j][j]) 獲得選擇平面矩陣J，使J * A *J'=A1 2. 計算得到A1後，重複第1歩，計算A2 =J2 *A1

形象理解線性代數（三）——列空間、零空間（核）、值域、特徵值（特徵向量）、矩陣與空間變換、矩陣的秩

這裡，我們還是要以形象理解線性代數（一）——什麼是線性變換？為基礎。矩陣對向量的作用，可以理解為線性變換，同時也可以理解為空間的變換，即（m*n）的矩陣會把一個向量從m維空間變換到n維空間。一、矩陣的列空間與矩陣的秩以及值域的關係矩陣的列空間，其實就是矩陣的列所組成的空間。比如我們考慮

線性代數（六）矩陣的特徵值與特徵向量——特徵值與特徵向量求解矩陣對角化

本節主要知識點 1.特徵向量與特徵值的定義：A為n階方陣，x為非零向量，Ax=λx，則λ為A的特徵值，x為A的屬於特徵值的特徵向量。 2.特徵值與特徵向量的求解過程（重點）寫出f(λ)=det(A-λI) 特徵值：計算f(λ)的全部根特徵向量：對A的每一個特徵值

【線性代數】矩陣的特徵分解、特徵值和特徵向量(eigen-decomposition, eigen-value & eigen-vector)

就像我們可以通過質因數分解來發現整數的一些內在性質一樣(12 = 2 x 2 x 3)，我們也可以通過分解矩陣來發現表示成陣列元素時不明顯的函式性質。矩陣分解有種方式，常見的有特徵分解 SVD 分解三角分解特徵分解特徵分解是使用最廣泛的

【線性代數公開課MIT Linear Algebra】第二十四課特徵值與特徵向量的應用——馬爾科夫矩陣、傅立葉級數

本系列筆記為方便日後自己查閱而寫，更多的是個人見解，也算一種學習的複習與總結，望善始善終吧~ 馬爾科夫矩陣Markov Matrix 馬爾科夫矩陣Markov Matrix有兩個性質：所有元素大於等於0，所有矩陣的列相加等於1。這裡性質導致一

【線性代數】矩陣、向量、行列式、特徵值與特徵向量（掌握這些概念一篇文章就夠了）

在數學領域中，線性代數是一門十分有魅力的學科，首先，它不難學；其次，它能廣泛應用於現實生活中；另外，在機器學習越來越被重視的現在，線性代數也能算得上是一個優秀程式設計師的基本素養吧？一、線性代數的入門知識很多人在大學學習線性代數時，國內

特徵值和特徵向量的幾何意義、計算及其性質

http://www.cnblogs.com/chaosimple/p/3179695.html 一、特徵值和特徵向量的幾何意義特徵值和特徵向量確實有很明確的幾何意義，矩陣（既然討論特徵向量的問題，當然是方陣，這裡不討論廣義特徵向量的概念，就是一般的特徵向量）乘以一

深度學習中的數學與技巧(7)：特徵值和特徵向量的幾何意義、計算及其性質

一、特徵值和特徵向量的幾何意義特徵值和特徵向量確實有很明確的幾何意義，矩陣（既然討論特徵向量的問題，當然是方陣，這裡不討論廣義特徵向量的概念，就是一般的特徵向量）乘以一個向量的結果仍是同維數的一個向量。因此，矩陣乘法對應了一個變換，把一個向量變成同維數的另一個向量。

數學基礎系列(五)----矩陣、矩陣的秩、向量、特徵值與特徵向量

一、矩陣 1、係數矩陣前面學習了矩陣很多基礎知識，那麼遇到具體的線性方程組該怎麼辦呢？該怎麼轉換為矩陣來求解呢？如下圖所示，A為係數矩陣，X是未知數矩陣，B是常數矩陣。　　 2、矩陣轉置簡單來說就是矩陣的行元素和列元素互相調換一下。　　下面列出一些矩陣轉置常用的公式　　這些都沒有什麼好說的

基於eigen計算矩陣的特徵值和特徵向量

有點小瑕疵，就是讀取檔案和生成檔案的位置！備註下本文是在Ubuntu系統下構建的，一些地方可能存在著差異。 1 首先是在如下的檔案下建立data.txt 這個檔案與源程式的檔案在同一個目錄下，其中data.txt的資料及其格式如下： 2 程式 #i

矩陣特徵值、特徵向量及其求解

相關推薦