位1的個數

編寫一個函式，輸入是一個無符號整數，返回其二進位制表示式中數字位數為 ‘1’ 的個數（也被稱為漢明重量）。 示例 : 輸入: 11 輸出: 3 解釋: 整數 11 的二進位制表示為 00000000000000000000000000001011

示例 2: 輸入: 128 輸出: 1 解釋: 整數 128 的二進位制表示為 00000000000000000000000010000000

思路：

將n的每一位與1進行與運算，為真就說明n的最後一位是1，n右移一位，左邊補0，直到n全部移除為0

c++程式碼

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;  
        while (
 
 n )  
        {  
            if( n & 1 ){  
                ++count;  
            }  
        n >>= 1; //右移一位 
        }  
        return count;
              
    }
};

漢明距離

兩個整數之間的漢明距離指的是這兩個數字對應二進位制位不同的位置的數目。 給出兩個整數 x 和 y，計算它們之間的漢明距離。 注意： 0 ≤ x, y < 231. 示例: 輸入: x = 1, y = 4

輸出: 2

解釋:

1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭頭指出了對應二進位制位不同的位置。

思路：

按位異或，不同的位置就變成了1，就看有多少個1，跟上題就一樣了

c++程式碼

class Solution {
public:
    int hammingDistance(int x, int y) {
        int count=0;
        int temp=x^y;//按位異或
        while(temp)
        {
            if(temp&1)
                count++;
            temp>>=
 
1;//右移一位
        }
        return count;
    }
};

顛倒二進位制位

顛倒給定的 32 位無符號整數的二進位制位。 示例: 輸入: 43261596 輸出: 964176192 解釋: 43261596 的二進位制表示形式為 00000010100101000001111010011100 ， 返回 964176192，其二進位制表示形式為 00111001011110000010100101000000 。 進階: 如果多次呼叫這個函式，你將如何優化你的演算法？

c++程式碼

class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        uint32_t m=0;
        for(int i=0;i<32;i++)
        {
            m<<=1;//m左移一位
            m=m|(n&1);//賦給m
            n>>=1;//n右移一位
        }
        return m;
    }
};

帕斯卡三角形

給定一個非負整數 numRows，生成楊輝三角的前 numRows 行。 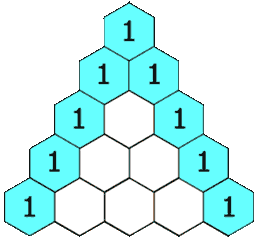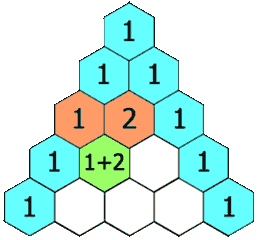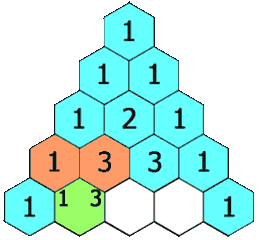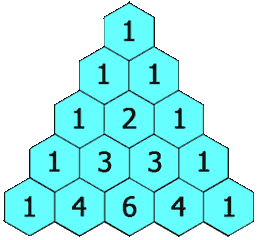在楊輝三角中，每個數是它左上方和右上方的數的和。 示例:

輸入: 5
輸出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

c++程式碼

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<int> row;
        vector<vector<int>> nums(numRows,row);
        for(int i=0;i<numRows;i++)
        {
            nums[i].push_back(1);
            for(int j=1;j<i;j++)
            {
                nums[i].push_back(nums[i-1][j]+nums[i-1][j-1]);
            }
            if(i>0)
                nums[i].push_back(1);
        }
        return nums;
            
    }
};

總是報錯reference binding to null pointer of type ‘value_type’ 查了查應該是對於vector構建出來的二維陣列沒有進行空間的申請,比如有些返回型別為vector<vector<>>型別的函式，對於這個返回值vector表示的二維陣列要先申請大小，否則使用下標訪問就會報這類錯誤。

有效的括號

給定一個只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字串，判斷字串是否有效。 有效字串需滿足： 左括號必須用相同型別的右括號閉合。 左括號必須以正確的順序閉合。 注意空字串可被認為是有效字串。 示例 1: 輸入: “()” 輸出: true 示例 2: 輸入: “()[]{}” 輸出: true 示例 3: 輸入: “(]” 輸出: false 示例 4: 輸入: “([)]” 輸出: false 示例 5: 輸入: “{[]}” 輸出: true

c++程式碼

class Solution {
public:
    bool isValid(string s) {
        stack<char> arr;
        for(int i=0;i<s.length();i++)
        {
            if(arr.empty())
                arr.push(s[i]);
            //能湊成一對就出棧
            else if(arr.top()=='('&&s[i]==')'||arr.top()=='['&&s[i]==']'||arr.top()=='{'&&s[i]=='}')
                arr.pop();
            else
                arr.push(s[i]);
        }
        if(arr.empty())
            return true;
        else
            return false;
    }
};

缺失數字

給定一個包含 0, 1, 2, …, n 中 n 個數的序列，找出 0 … n 中沒有出現在序列中的那個數。 示例 1: 輸入: [3,0,1] 輸出: 2 示例 2: 輸入: [9,6,4,2,3,5,7,0,1] 輸出: 8 說明: 你的演算法應具有線性時間複雜度。你能否僅使用額外常數空間來實現?

c++程式碼

方法一： 新建一個0-n的陣列flag，下標代表n個數，值代表是否存在這個數，開始都設為0，表示不存在這個數，遍歷一遍nums，將所有遇到的都設為1.最後為0的就是沒有出現的。但是這個空間複雜度O(n)

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        if(nums.empty())
            return 0;
        int n=nums.size();
        vector<int> flag;
        for(int i=0;i<=n;i++)
        {
            flag.push_back(0);
        }         
        for(int i=0;i<n;i++)
        {
            flag[nums[i]]=1;
        }
        for(int j=0;j<=n;j++)
        {
            if(flag[j]==0)
                return j;
        }
        
    }
};

方法二： 不缺失數字時候的加和可以計算，缺失數字之後的加和遍歷一遍也可以計算出來，二者相減不就是缺失的數字了

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        if(nums.empty())
            return 0;
        int sum=0,sum2=0;
        int n=nums.size();
        //缺失數字的加和
        for(int i=0;i<n;i++)
            sum=sum+nums[i];
        //未缺失數字加和
        for(int i=0;i<n+1;i++)
        {
            sum2=sum2+i;
        }
        return sum2-sum;
        
    }
};