Java集合原始碼解析:TreeMap
本文概要
- 二叉查詢樹的用處
- 二叉查詢樹,以及二叉樹帶來的問題
- 平衡二叉樹的好處
- 紅黑樹的定義以及構造
- 紅黑樹在TreeMap的運用
二叉樹的好處
可能許多人會有疑問,為什麼要使用二叉樹,有那麼多的資料結構,比如陣列、連結串列等
簡單看下陣列和連結串列的優缺點
陣列
- 優勢:查詢快,通過索引直接定位資料。時間複雜度O(1)
- 劣勢:刪除和插入元素比較麻煩,需要移動的元素比較多。時間複雜度O(n)
連結串列
- 優勢:刪除和插入比較方便,直接修改指標,時間複雜度O(1)
- 劣勢:查詢慢,需要沿著頭指標挨個去對比,時間複雜度O(n)
那麼二叉樹則是結合了上面兩種資料結構的優勢,並且它是有序的,而且在處理大批量的動態資料是比較有用的。它的時間複雜度O(logN)
二叉查詢樹
先來看看二叉查詢樹的定義:
- 要麼是一顆空樹,要麼就是一顆具有如下特性的二叉樹
- 左節點的值必須小於等於父節點的值
- 右節點的值必須大於等於父節點的值
每個節點都符合這個特性,所以它是有序的,也便於查詢,如下圖:
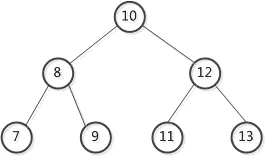
但是在一種極端的情況下,二叉查詢樹會出現不平衡。如果一棵二叉樹,只有左子樹或者右子樹,就變成了一個連結串列,查詢的效率就變的很慢,如下圖:

對於查詢而言,二叉查詢樹的查詢是跟樹的高度是有關係的,如果一棵樹的高度為N,那麼最多可以在N步內完成查詢,所以樹的高度越矮,那麼查詢的效率就越高。考慮到一般情況,左子樹和右子樹的高度不能相差太大,所以我們都希望二叉查詢樹兩邊子樹是平衡的,而不是隻有一邊子樹。為了優化因左右子樹高度不穩定對查詢效率的影響,於是出現了平衡二叉樹
平衡二叉樹
先看平衡二叉樹的定義:
- 它是一顆二叉樹
- 它的左子樹和右子樹的深度差的絕對值不超過1

在構造平衡二叉樹時,新增一個節點,可能會造成二叉樹的失衡,失衡調整主要是通過旋轉最小失衡樹來實現。
失衡調整主要分為4種情況:
- LL型

當插入“7”節點,是最小失衡樹的左子樹的“8”左節點。很顯然,是“9”的左子樹過高,那麼以"9"節點為軸心右旋
- LR型

當插入"8"節點,是最小失衡樹左子樹的“7”的右節點。首先以“7”為軸心,然後左旋,變成了LL型,然後以“9”為軸心右旋。
-
RR型
 當插入“11”節點,是最小失衡樹的右子樹的“10”右節點。很顯然,是“9”的右子樹過高,那麼以"9"節點為軸心左旋
當插入“11”節點,是最小失衡樹的右子樹的“10”右節點。很顯然,是“9”的右子樹過高,那麼以"9"節點為軸心左旋 -
RL型

當插入"11"節點,是最小失衡樹右子樹的“12”的左節點。首先以“12”為軸心,右旋,變成了RR型,然後以“10”為軸心右旋。
紅黑樹
先來看看紅黑樹的定義
- 每個節點要麼紅色,要麼黑色
- 根節點是黑色
- 所有葉子節點是黑色,即空節點(NIL)
- 每個紅色節點的兩個子節點都是黑色(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)
- 從一個節點到其所有葉子節點的所有路徑上包含相同數目的黑節點
注意:
- 特性3中的葉子節點,是隻為空(NIL或null)的節點。
- 特性5,確保沒有一條路徑會比其他路徑長出倆倍。因而,紅黑樹是相對是接近平衡的二叉樹。因此在最壞情況下,紅黑樹能保證時間複雜度為O( lgn )

當對紅黑樹進行插入和刪除時,可能會破壞紅黑樹的性質,那麼就需要通過修改某些節點顏色和樹的旋轉來恢復紅黑樹的性質
樹的旋轉,分為左旋和右旋,如下圖
-
左旋
 對A節點進行左旋,首先找到A節點的右孩子節點B,讓B節點的左孩子節點C指向A節點的右孩子節點,再把A節點指向B節點的左孩子節點。
對A節點進行左旋,首先找到A節點的右孩子節點B,讓B節點的左孩子節點C指向A節點的右孩子節點,再把A節點指向B節點的左孩子節點。 -
右旋

對A節點進行右旋,首先找到A節點的左孩子節點B,讓B節點的右孩子節點D執行A節點的右孩子節點,在把A節點執行B節點的右孩子節點。
紅黑樹的插入
向一棵含有n個節點的紅黑樹插入一個新節點的操作可以在O(lgn)時間內完成。 在繼續插入操作分析前,再來複習下紅黑樹的特性:
- 每個節點要麼紅色,要麼黑色
- 根節點是黑色
- 所有葉子節點是黑色,即空節點(NIL)
- 每個紅色節點的兩個子節點都是黑色(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)
- 從一個節點到其所有葉子節點的所有路徑上包含相同數目的黑節點
規則:
- 在紅黑樹插入節點時,節點的初始顏色是紅色,這樣可以儘量避免對樹的結構進行調整(參考第5個規則)
- 但是插入紅色節點的時候,不會破壞第5個規則,但是可能會破壞第4個規則,所以這時候就需要通過修改某些節點的顏色、對某些節點進行旋轉,來維持紅黑樹的性質
- 在刪除節點是時候,如果刪除的節點為黑色,可能會破壞第5個規則,那麼同樣需要修復樹的結構,以進行維護樹的性質
插入節點可以分為7種情況進行處理
- 空樹中插入節點
- 插入節點的父節點是黑色
- 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是左節點,父節點是左節點
- 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是左節點,父節點是右節點
- 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是右節點,父節點是右節點
- 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是右節點,父節點是左節點
- 插入節點的父節點是紅色,且叔叔節點也是紅色
情況一:空樹中插入節點
違反:性質2
修復策略:把插入節點修改為黑色即可
情況二:插入節點的父節點是黑色
違反:未違反任何性質
修復策略:什麼都不做
情況三: 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是左節點,父節點是左節點
違反:性質4
修復策略:
- 把父節點顏色修改為黑色
- 把祖父節點顏色修改為紅色
- 對祖父節點進行右旋
如下圖所示:

情況四: 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是左節點,父節點是右節點
違反:性質4
修復策略:
- 對父節點進行右旋
- 把自己節點顏色修改為黑色,祖父節點修改為紅色
- 對祖父節點進行左旋
如下圖:

情況五: 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是右節點,父節點是右節點
違反:性質4
修復策略:
- 把父節點顏色修改為黑色
- 把祖父節點顏色修改為紅色
- 對祖父節點進行左旋
圖就不畫,跟情況三型別
情況六: 插入節點的父節點是紅色,且叔叔節點是黑色,當前節點是右節點,父節點是左節點
違反:性質4
修復策略:
- 對父節點進行左旋
- 把自己節點修改為黑色,把祖父節點顏色修改為紅色
- 對祖父節點進行右旋
圖就不畫,跟情況四型別
情況七: 插入節點的父節點是紅色,且叔叔節點是紅色
違反:性質4
修復策略:
- 把父節點顏色和叔叔節點顏色修改為黑色
- 把祖父節點顏色修改為紅色
- 然後會變成情況一至七的情況,繼續按情況進行分析
刪除節點對節點的調整,我們在TreeMap在進行分析
TreeMap
Java TreeMap實現了SortedMap介面,也就是說會按照key的大小順序對Map中的元素進行排序,key大小的判定通過其本身自帶的自然排序,也可以通過構造器傳入Comparator比較器。
TreeMap底層是通過紅黑樹實現,也就意味著containsKey(),get(),put(),remove()的時間複雜度都為O(log(n))
首先來看看TreeMap構造器
public TreeMap() {
comparator = null;
}
public TreeMap(Comparator<? super K> comparator) {
this.comparator = comparator;
}
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
}
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
TreeMap的成員變數
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable
{
// key的比較器
private final Comparator<? super K> comparator;
// 樹的根節點
private transient Entry<K,V> root;
// 樹的節點個數
private transient int size = 0;
// 對樹的修改次數
private transient int modCount = 0;
````省略程式碼
}
下面我們依次來看get()、put()、remove()方法
get()
public V get(Object key) {
// get方法實際上呼叫的是getEntry()
Entry<K,V> p = getEntry(key);
// 如果p節點存在,則返回p節點的value,否則返回null
return (p==null ? null : p.value);
}
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
// 如果建立TreeMap的時候傳入了比較器,那麼呼叫getEntryUsingComparator(key)
// getEntryUsingComparator(key)跟getEntry(key)邏輯差不多,只不過一個使用了自定義比較器去比較key,一個使用自身的比較器去比較key
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
// 把key強轉為比較器
Comparable<? super K> k = (Comparable<? super K>) key;
// 獲取根節點
Entry<K,V> p = root;
while (p != null) {
// key與根節點的key進行比較
int cmp = k.compareTo(p.key);
if (cmp < 0)
// key小,則把左節點賦給p進行迴圈
p = p.left;
else if (cmp > 0)
// key大,則把右節點賦給p進行迴圈
p = p.right;
else
// 相等,直接返回p節點
return p;
}
return null;
}
get()方法還是比較簡單的,從根節點開始,依次對節點的key進行判斷,如果大於節點的key則繼續判斷節點的右孩子節點,以此類推,直到找到相等key的節點。上面都有註釋講的非常清楚了。
put()
public V put(K key, V value) {
Entry<K,V> t = root;
// 如果根節點為空
if (t == null) {
compare(key, key); // type (and possibly null) check
// 直接建立一個Entry,賦給根節點
root = new Entry<>(key, value, null);
// 樹節點的大小賦值為1
size = 1;
// 修改次數+1
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
// 獲取比較器
Comparator<? super K> cpr = comparator;
// 判斷該key是否存在,如果存在直接找到該節點,把節點的值修改為新value,然後直接返回
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 如果key不存在
// 建立一個新的Entry節點
Entry<K,V> e = new Entry<>(key, value, parent);
// key與parent的key進行比較
if (cmp < 0)
// key小,把新節點指向parent的左節點
parent.left = e;
else
// key大,把新節點指向parent的右節點
parent.right = e;
// 添加了一個紅色的新節點,可能會破壞原來的紅黑樹結構,那麼需要進行修復
fixAfterInsertion(e);
// 節點+1
size++;
// 修改次數+1
modCount++;
return null;
}
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
put()方法總結:
- 首先獲取樹根節點,如果根節點為空,那麼直接建立一個新節點指向根節點
- 根節點不為空,然後判斷樹裡面是否存在節點的key與新增的key相等
- 如果相等,那麼直接把該節點的value替換成新的value
- 如果不相等,然後建立一個新的節點,新增到紅黑樹中
- 添加了一個新的節點可能會破壞樹的結構,那麼呼叫fixAfterInsertion(),進行紅黑樹結構進行調整。
fixAfterInsertion()跟我們在上面講紅黑樹插入的情況,已經講的非常清楚了。
remove()
public V remove(Object key) {
// 首先判斷該key是否存在
Entry<K,V> p = getEntry(key);
if (p == null)
// 不存在直接返回null
return null;
V oldValue = p.value;
// 呼叫deleteEntry()刪除節點
deleteEntry(p);
return oldValue;
}
private void deleteEntry(Entry<K,V> p) {
// 修改次數+1
modCount++;
// 樹節點個數-1
size--;
// 如果p節點的左右孩子節點都不為空,那麼呼叫successor(p)尋找後繼節點
if (p.left != null && p.right != null) {
// 尋找後繼節點邏輯很簡單
// 即為:p節點的右子樹的最小的那個元素,即為p的後繼節點
Entry<K,V> s = successor(p);
// 把p替換成後繼節點
p.key = s.key;
p.value = s.value;
p = s;
}
// 獲取p節點的左孩子節點,如果左孩子節點不存在,則獲取p節點的右孩子節點
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
// 如果p節點的孩子節點不為空
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) {
// 如果p的父節點為null,則為root節點
root = null;
} else {
// 如果p節點沒有孩子節點
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
successor(),找到後繼節點
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
Entry<K,V> p = t.right;
// 沿著t的右節點的左子樹找到最小的元素
while (p.left != null)
p = p.left;
return p;
} else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
找到後繼節點原理很簡單,就是沿著右孩子節點的左子樹找到最小的元素
fixAfterDeletion(),對刪除節點的樹,進行修復
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) ==
