題目大意

輸入n、w、h（1≤n≤10，1≤w，h≤n），求能放在w*h網格里的不同的n連塊的個數（注意，平移、旋轉、翻轉後相同的算作同一種）。例如，2*4裡的5連塊有5種（第一行），而3*3裡的8連塊有以下3種（第二行）。

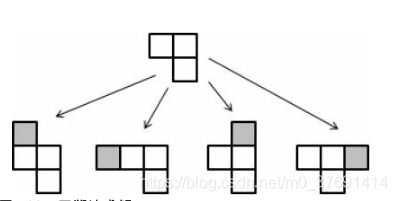
題目解析

本題難點在於如何判重，如果採用最簡單的寫法，每個n連塊都會被重複列舉很多次。那麼有沒有好的方法只判重一次呢？答案是當然有的呀，畢竟人類的智慧是無窮無盡的。那麼是什麼方法的，現在由主角

如何用資料結構表示圖形呢？

其實很簡單啦，我們關心的使圖形的形狀而不是位置，每一個圖形都是由若干個格子聯通，那麼我們只需要記錄下n個格子的位置，其整體表示就是圖形的形狀啦。對於格子位置的儲存，不必造輪子啦，只需要用我們強大的set<Cell>

那麼現在來解決的三大難題之圖形的平移、旋轉、翻轉

1、對於平移操作，我們可以定義一個normalize函式，找出x,y分別的最小值minX,minY，那麼它可以視為一個平移向量 (minX,minY)，將連通塊的每個單元格都減去該向量，即實現了標準化。

2、對於旋轉操作，我們可以定義一個rotate函式，表示將整個連通塊圍繞座標原點順時針旋轉90度。如何實現呢？只需要將每個格子都順時針旋轉90度即可。相應的幾何變換為(x,y)->(y,-x)。

3、對於翻轉操作，由於既可以沿x軸翻轉，也可以沿y軸翻轉，但實際上沿x軸翻轉後再繞座標原點順時針旋轉180度即可得到沿y軸翻轉的圖案。因此這裡我們定義一個flip函式，表示將一個連通塊沿x軸翻轉。相應的幾何變換為(x,y)->(x,-y)。

那麼如何推出n個格子組成的圖形有多少種呢？

當n>1時，一定是在n-1連通塊的基礎上生成的，即以每個n-1連通塊為基礎，以某一個n-1 連通塊的某個單元格開始，向上下左右4個方向擴充套件。如果可以擴充套件，且不出現重複，就找到了一個n連通塊，加入到集合中來。最終完成n連通塊的列舉。（這也是我們的打表技術啦）

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<set>
using namespace std;
struct Cell{
	int x, y;
	Cell(int x = 0, int y = 0):x(x), y(y){}
	bool operator < (const Cell rhs) const {
		return x < rhs.x || (x == rhs.x && y < rhs.y);
	}
};
typedef set<Cell> Polyomino;
#define FOR_CELL(c, p) for(Polyomino::const_iterator c = (p).begin(); c != (p).end(); ++c)

inline Polyomino normalize(const Polyomino &p){ //標準化
	Polyomino q;
	int minX = p.begin()->x, minY = p.begin()->y;
	FOR_CELL(c, p){
		minX = min(minX, c->x);
		minY = min(minY, c->y);
	}
	FOR_CELL(c, p){
		q.insert(Cell(c->x - minX, c->y - minY));
	}
	return q;
}
inline Polyomino rotate(const Polyomino &p){ //順時針旋轉90度
	Polyomino q;
	FOR_CELL(c, p){
		q.insert(Cell(c->y, -c->x));
	}
	return normalize(q);
}
inline Polyomino flip(const Polyomino &p){ //向x軸翻轉
	Polyomino q;
	FOR_CELL(c, p)
		q.insert(Cell(c->x, -c->y));
	return normalize(q);
}

int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, -1, 1};
const int maxn = 11;
set<Polyomino> Poly[maxn];
int ans[maxn][maxn][maxn];
inline bool flipInFourDir(Polyomino &p, const int &n){ //360 = 90 * 4度旋轉
	for(int i = 0; i < 4; ++i){
		if(Poly[n].count(p) != 0) return false;
		p = rotate(p);
	}
	return true;
}
void checkPolyomino(const Polyomino &p, const Cell &c){ 
	Polyomino q = p;
	q.insert(c);
	q = normalize(q);
	int n = q.size();
	if(flipInFourDir(q, n) == false) return;
	q = flip(q);
	if(flipInFourDir(q, n) == false) return;
	Poly[n].insert(q);
}
void generate(){
	Polyomino p;
	p.insert(Cell(0, 0));
	Poly[1].insert(p);
	for(int n = 2; n < maxn; ++n){
		for(set<Polyomino>::iterator s = Poly[n - 1].begin(); s != Poly[n - 1].end(); ++s){
			FOR_CELL(c, *s){
				for(int i = 0; i < 4; ++i){
					Cell newc(c->x + dx[i], c->y + dy[i]);
					if((*s).count(newc) == 0) checkPolyomino(*s, newc);
				}
			}
		}
	}

	for(int n = 1; n < maxn; ++n){
		for(int w = 1; w < maxn; ++w){
			for(int h = 1; h < maxn; ++h){
				int cnt = 0;
				for(set<Polyomino>::iterator s = Poly[n].begin(); s != Poly[n].end(); ++s){
					int maxX = 0, maxY = 0;
					FOR_CELL(c, *s){
						maxX = max(maxX, c->x);
						maxY = max(maxY, c->y);
					}
					if(min(h, w) > min(maxX, maxY) && max(h, w) > max(maxX, maxY)) ++cnt;
				}
				ans[n][w][h] = cnt;
			}
		}
	}
}
int main(){
	generate();
	int n, w, h;
	freopen("data.in", "r", stdin);
	while(scanf("%d%d%d", &n, &w, &h) == 3){
		printf("%d\n", ans[n][w][h]);
	}
	return 0;
}