（一）前 言

一元線性迴歸是一個主要影響因素作為自變數來解釋因變數的變化，但在現實問題中，因變數的變化往往受到多個重要因素的影響，這時就需要兩個或兩個以上的影響因素作為自變數來解釋因變數的變化，這便是多元迴歸，而當多個自變數與因變數之間是線性關係時，所進行的迴歸分析就是多元線性迴歸。多元線性迴歸的一般形式為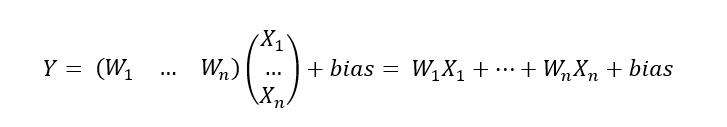： 同一元線性迴歸一樣，我們要在誤差平方和最小的情況下，使用最小二乘法求解引數，下面我們通過一個預測房屋租賃價格的例項來透徹理解多元線性迴歸模型。

（二）資料展示

在此例中房屋租賃價格為因變數，房屋面積和房屋數量為自變數，由4.1可知，此處我們要建立一個二元線性迴歸模型，首先構建訓練資料集，並對其進行視覺化。

構建資料集
x1_data = np.random.randn(100).astype(np.float32)# 生成100個[0，1）間的隨機數
x2_data = np.random.randn(100).astype(np.float32)# 房屋面積
y_data = x1_data * 2 + x2_data * 3 + 1.5 # 房屋價格

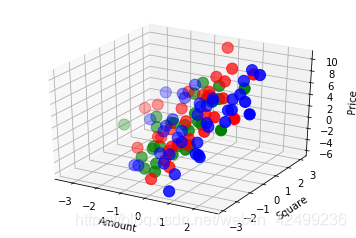繪圖程式碼:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 匯入3D繪相簿
x1_data = np.random.
 
randn(100).astype(np.float32)# 生成100個[0，1）間的隨機數
x2_data = np.random.randn(100).astype(np.float32)
y_data = x1_data+ x2_data + 1.5 
x, y, z = x1_data, x2_data, y_data
ax = plt.subplot(111, projection='3d')# 建立一個三維的繪圖工程
# 將資料點分成三部分畫，在顏色上有區分度
ax.scatter(x[:30], y[:30], z[:30], c='g',s = 125)  # 繪製資料點
ax.scatter(
 
x[30:60], y[30:60], z[30:60], c='r',s = 125)
ax.scatter(x[60:100], y[60:100], z[60:100], c='b',s = 125)
ax.set_zlabel('Price')# 設定座標軸
ax.set_ylabel('Square')
ax.set_xlabel('Amount')
plt.show()

（三）模型的TensorFlow實現

（1）模型引數設定

# 設定學習率
learning_rate = 0.01
# 設定最小誤差
threshold = 0.01

（2）輸入資料

# 構造訓練資料
x1_data = np.random.randn(100).astype(np.float32)
x2_data = np.random.randn(100).astype(np.float32)
y_data = 2 * x1_data + 3 * x2_data + 1

（3）構建模型

weight1 = tf.Variable(1.)
weight2 = tf.Variable(1.)
bias = tf.Variable(1.)
x1_ = tf.placeholder(tf.float32)
x2_ = tf.placeholder(tf.float32)
y_ = tf.placeholder(tf.float32)
# 構建模型Y = weight1 * X1 + weight2 * X2 + Bias
y_model = tf.add(tf.add(tf.multiply(weight1, x1_), tf.multiply(weight2, x2_)), bias)

（4）定義損失函式

# 採用均方差做為損失函式
loss = tf.reduce_mean(tf.pow((y_model - y_), 2))

（5）選擇優化器及定義訓練操作

# 使用隨機梯度下降演算法
train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

（6）建立會話進行訓練

with tf.Session() ,as ,sess:
# 引數初始化
    sess.run(tf.global_variables_initializer())
# 開始訓練
    print("Start training!")
    flag = 1
    while(flag):
# 使用zip進行巢狀，表示三個引數
         for (x,y) in zip(zip(x1_data, x2_data), y_data):
              sess.run(train_op, feed_dict = {x1_ : x[0],x2_ : x[1],y_ : y})
# 當訓練損失低於threshold時停止訓練
              if sess.run(loss, feed_dict = {x1_ : x[0],x2_ : x[1],y_ : y}) < threshold:
                  flag = 0
	w1 = sess.run(weight1)
	w2 = sess.run(weight2)
	b = sess.run(bias)
	print('n')
	print('線性迴歸方程為：')
	print("Y = %f * X1 + %f * X2 + %f " % (w1, w2, b))
	print('n')
	# 繪製模型圖
	fig = plt.figure()
	ax = Axes3D(fig)
	X, Y = np.meshgrid(x1_data, x2_data)
	Z = sess.run(weight1) * (X) + sess.run(weight2) * (Y) + sess.run(bias)
	ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1, cmap = plt.cm.hot)
	ax.contourf(X, Y, Z, zdir = 'z', offset = -1, camp = plt.cm.hot)
	ax.set_title('analysis')
	ax.set_ylabel('salary')
	ax.set_xlabel('age')
	ax.set_zlabel('amount')
	ax.set_zlim(-1, 1)
	plt.show()

（7）訓練結果

在學習率為0.01時，經過若干次迭代後，總體誤差小於0.01，最終得到的模型為：

Y = 1.894042 * X1 + 2.866999 * X2 + 1.003049

實際模型為：

Y = 2 * X1 + 3 * X2 + 1

進行視覺化，得：

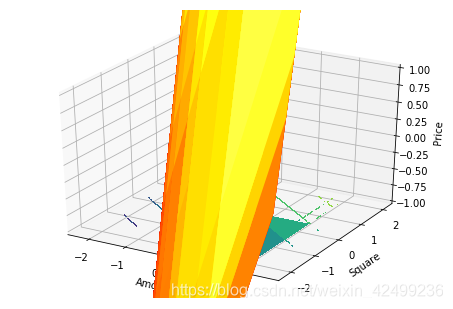
（8）完整程式碼

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D#呼叫matplotlib的3D繪圖功能
# 設定學習率
learning_rate = 0.01
# 設定最小誤差
threshold = 0.01
# 構造訓練資料
x1_data = np.random.randn(100).astype(np.float32)
x2_data = np.random.randn(100).astype(np.float32)
y_data = 2 * x1_data + 3 * x2_data + 1
# 構建模型
weight1 = tf.Variable(1.)
weight2 = tf.Variable(1.)
bias = tf.Variable(1.)
x1_ = tf.placeholder(tf.float32)
x2_ = tf.placeholder(tf.float32)
y_ = tf.placeholder(tf.float32)
# 構建模型Y = weight1 * X1 + weight2 * X2 + Bias
y_model = tf.add(tf.add(tf.multiply(weight1, x1_), tf.multiply(weight2, x2_)), bias)
# 採用均方差做為損失函式
loss = tf.reduce_mean(tf.pow((y_model - y_), 2))
# 使用隨機梯度下降演算法
train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
with tf.Session() as sess:
# 引數初始化
    sess.run(tf.global_variables_initializer())
# 開始訓練
    print("Start training!")
    flag = 1
    while(flag):
# 使用zip進行巢狀，表示三個引數
         for (x,y) in zip(zip(x1_data, x2_data), y_data):
              sess.run(train_op, feed_dict = {x1_ : x[0],x2_ : x[1],y_ : y})
# 當訓練損失低於threshold時停止訓練
              if sess.run(loss, feed_dict = {x1_ : x[0],x2_ : x[1],y_ : y}) < threshold:
                  flag = 0
	w1 = sess.run(weight1)
	w2 = sess.run(weight2)
	b = sess.run(bias)
	print('n')
	print('線性迴歸方程為：')
	print("Y = %f * X1 + %f * X2 + %f " % (w1, w2, b))
	print('n')
	# 繪製模型圖
	fig = plt.figure()
	ax = Axes3D(fig)
	X, Y = np.meshgrid(x1_data, x2_data)
	Z = sess.run(weight1) * (X) + sess.run(weight2) * (Y) + sess.run(bias)
	ax.plot_surface(X, Y, Z, rstride = 1, cstride = 1, cmap = plt.cm.hot)
	ax.contourf(X, Y, Z, zdir = 'z', offset = -1, camp = plt.cm.hot)
	ax.set_title('analysis')
	ax.set_ylabel('salary')
	ax.set_xlabel('age')
	ax.set_zlabel('amount')
	ax.set_zlim(-1, 1)
	plt.show()

（四）總 結

本文通過建立二元線性迴歸模型解決了房屋租賃價格的問題，給出了使用TensorFlow建立多元線性迴歸模型的一般方法，讀者遇到其他需要多元線性迴歸模型解決的問題時，可仿照上述過程進行程式碼修改即可，有任何疑問請在評論區留言，我會盡快回復，謝謝支援！