【Paper】Deep & Cross Network for Ad Click Predictions
目錄
背景
探索具有預測能力的組合特徵對提高CTR模型的效能十分重要,這也是大量人工特徵工程存在的原因。但是資料高維稀疏(大量離散特徵one-hot之後)的性質,對特徵探索帶來了巨大挑戰,進而限制了許多大型系統只能使用線性模型(比如邏輯迴歸)。線性模型簡單易理解並且容易擴充套件,但是表達能力有限,對模型表達能力有巨大作用的組合特徵通常需要人工不斷的探索。深度學習的成功激發了大量針對它的表達能力的理論分析,研究顯示給定足夠多隱藏層或者隱藏單元,DNN能夠在特定平滑假設下以任意的精度逼近任意函式。實踐中大多數函式並不是任意的,所以DNN能夠利用可行的引數量達到很好的效果。DNN憑藉Embedding向量以及非線性啟用函式能夠學習高階的特徵組合,並且殘差網路的成功使得我們能夠訓練很深的網路。
相關工作
由於資料集規模和維度的急劇增加,為了避免針對特定任務的大規模特徵工程,湧現了很多方法,這些方法主要是基於Embedding和神經網路技術。
- FM將稀疏特徵對映到低維稠密向量上,通過向量內積學習特徵組合,也就是通過隱向量的內積來建模組合特徵。
- FFM在FM的基礎上引入Field概念,允許每個特徵學習多個向量,針對不同的Field使用不同的隱向量。
- DNN依靠神經網路強大的學習能力,能夠自動的學習特徵組合,但是它隱式的學習了所有的特徵組合,這對於模型效果和學習效率可能是不利的。
遺憾的是FM和FFM的淺層結構限制了它們的表達能力(兩者都是針對低階的特徵組合進行建模),也有將FM擴充套件到高階的方法,但是這些方法擁有大量的引數產生了額外的計算開銷。Kaggle競賽中,很多取勝的方法中人工構造的組合特徵都是低階的,並且是顯性(具有明確意義)高效的。而DNN學習到的都是高度非線性的高階組合特徵,含義難以解釋。是否有一種模型能夠學習有限階數的特徵組合,並且高效可理解呢?本文提出的DCN就是一種。W&D也是這種思想,組合特徵作為線性模型的輸入,同時訓練線性模型和DNN,但是該模型的效果取決於組合特徵的選擇。
主要貢獻
交叉網路是個多層網路,能夠有效的學習特定階數的特徵組合,特徵組合的最高階數取決於網路層數。通過聯合(jointly)訓練交叉網路和DNN,DCN保留了DNN捕獲複雜特徵組合的能力。DCN不需要人工特徵工程,而且相對於DNN來說增加的複雜度也是微乎其微。實驗表明DCN在模型準確度和記憶體使用方面具有優勢,需要比DNN少一個數量級的引數。
- 支援稀疏、稠密輸入,能夠高效的學習特定階數限制下的特徵組合以及高階非線性特徵組合,並且不需要人工特徵工程,擁有較低的計算開銷;
- 交叉網路簡單有效,特徵組合的最高階數取決於網路層數,網路中包含了1價到特定階數的所有項的組合並且它們的係數不同;
- 節省記憶體並且易於實現,擁有比DNN低的logloss,而且引數量少了近一個數量級。
核心思想
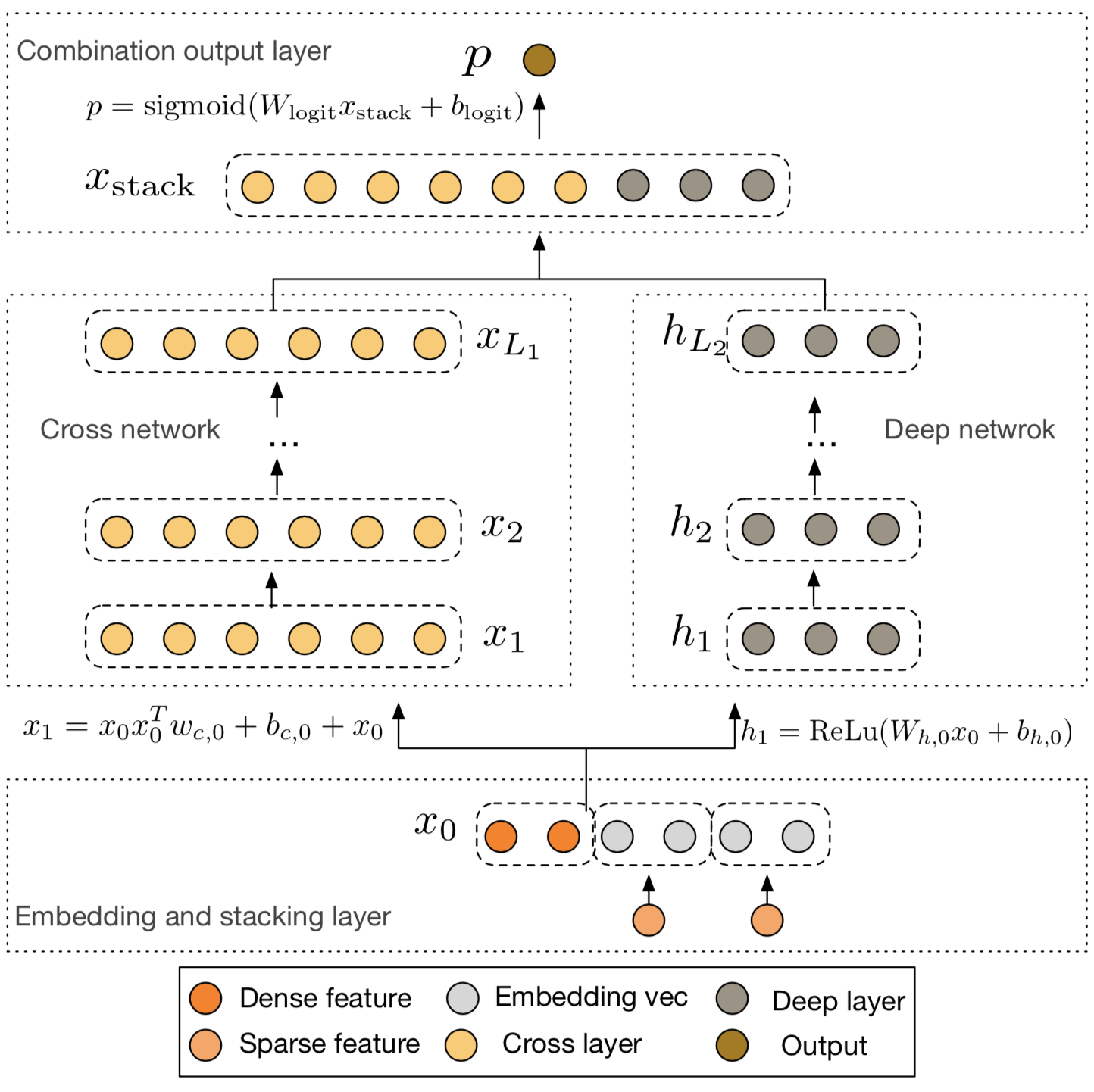
Embedding和Stacking層
模型的輸入大部分是類別特徵,這種特徵通常會進行one-hot編碼,這就導致了特徵空間是高維稀疏的(比如ID特徵經過one-hot編碼之後)。為了降低維度,通常會利用Embedding技術將這些二值特徵轉變成實值的稠密向量(Embedding向量)。Embedding過程用到的引數矩陣會和網路中的其它引數一塊進行優化。最後將這些Embedding向量和經過歸一化的稠密特徵組合(stack)到一起作為網路的輸入。 \[X_0=[X_{embed,1}^T,\dots,X_{embed,k}^T,X_{dense}^T]\]
交叉網路(Cross Network)

交叉網路的核心思想是以一種高效的方式進行顯性的特徵組合,每一層的神經元數量都相同而且等於輸入向量\(X_0\)的維度,每一層都符合下面公式(都是列向量),其中函式\(f\)擬合的是\(X_{l+1}-X_l\)的殘差。 \[X_{l+1} = X_0X_l^TW_l+B_l+X_l=f(X_l,W_l,B_l)+X_l\] \(l\)層的交叉網路組成了\((x_1,\dots,x_d)\)從1價到\(l+1\)價所有的特徵組合。另\(L_c\)表示交叉網路的層數,\(d\)表示輸入向量的維度,則交叉網路需要的引數為\(d \times L_c \times 2\),乘以2是因為每一層有兩個長度為\(d\)的引數\(W\)和\(B\),從而交叉網路的時空複雜度為\(O(d)\),所以交叉網路相對於DNN引入的複雜度是微乎其微的。得益於\(X_0X_l^T\)的一階性質,使得我們無需計算和儲存整個矩陣就能夠高效的生成所有交叉項。
深度網路(Deep Network)
交叉網路小規模的引數限制了模型的表達能力,為了獲得高度非線性的組合特徵,我們引入了DNN,該網路是一個全聯接前饋神經網路,每一層都符合下面公式,其中\(H_l\)表示隱藏層,\(f(\cdot)\)是ReLU啟用函式。 \[H_{l+1} = f(W_lH_{l}+B_l)\] 為了簡單起見假設每個隱藏層的神經元數目相同,另\(L_d\)表示層數\(m\)表示每層的神經元個數,則第一層需要的引數量為\(d\times m + m\),剩餘層需要的引數量為\((m^2 +m)\times (L_d -1)\)。
組合層(Combination Layer)
組合層將交叉網路和DNN的輸出組合到一塊,然後將組合向量輸入標準的logits層,用下面的公式解決二分類問題,其中$\sigma (x)=1/(1+exp(-x)) $。 \[p=\sigma ([X_{L_d} ^ T,H_{L_m}^T]\cdot W_{logits} + B_{logits})\] 損失函式如下式,其中\(p_i\)是通過上式計算出來的正例的概率,然後通過聯合訓練(jointly)交叉網路和DNN,使得兩個網路在訓練階段知道彼此的存在。 \[loss = -\frac{1}{N} \sum_{i=1}^N y_i log(p_i) + (1-y_i)log(1-p_i) + \lambda \sum_{l} ||w_l||^2\]
理論分析
多項式近似
根據Weierstrass逼近定理,在特定平滑假設下任意函式都可以被一個多項式以任意的精度逼近,所以可以從多項式近似的角度分析交叉網路。\(d\)元\(n\)階多項式引數量為\(O(d^n)\),交叉網路只需要\(O(d)\)引數量就可以生成相同階數多項式中出現的所有交叉項。
FM的泛化
交叉網路借鑑了FM共享引數的思想並將它擴充套件至更深的結構。FM模型中每個特徵\(x_i\)都有一個相關的權重向量\(v_i\),交叉項\(x_ix_j\)的權重通過\(<v_i,v_j>\)計算得到。DCN中每個特徵\(x_i\)都對應一個標量集\(\lbrace w_k^{(i)} \rbrace _{k=0}^l\),也就是每個交叉層權重向量\(W\)的第\(i\)分量組成的集合,這樣交叉項\(x_ix_j\)的權重通過\(\lbrace w_k^{(i)} \rbrace _{k=0}^l\)和\(\lbrace w_k^{(j)} \rbrace _{k=0}^l\)計算得到。兩個模型中每個特徵對應的引數都是獨立學習的,交叉項的引數通過對應的特徵引數計算得到。引數共享不僅使得模型更高效而且對沒見過的組合特徵具有更好的泛化能力,同時對噪聲更健壯。比如\(x_i\)和\(x_j\)在訓練資料中沒有同時出現過,\(x_ix_j\)對應的權重就無法學習到。FM是一個淺層結構,只能表示2價的特徵組合。DCN能夠學習高階的特徵組合,在特定階數限制下能夠構建所有的交叉項。而且同對FM的高階擴充套件相比,DCN的引數量是輸入向量維度的線性函式。
高效對映
每個交叉層都會建立\(X_0\)和\(X_l\)各元素之間的兩兩組合,生成\(d^2\)維度的向量,然後將該向量對映到\(d\)維的空間中。如果直接進行對映操作需要\(O(d^3)\),而DCN提供了一種高效的對映方式只需要\(O(d)\)即可。考慮\(X_p=X \tilde X^T W\),假設\(X\)和\(W\)都是2維列向量,如下所示上面公式是直接計算,下面公式是高效的計演算法法。 \[ X_p = X \tilde X^T W = \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} [\tilde x_1, \tilde x_2] W = \begin{bmatrix}x_1 \tilde x_1 & x_1 \tilde x_2 \\ x_2 \tilde x_1 & x_2 \tilde x_2 \\ \end{bmatrix} W \]
\[ X_p ^T = [x_1 \tilde x_1,x_1 \tilde x_2, x_2 \tilde x_1, x_2 \tilde x_2] \begin{bmatrix} W & 0 \\ 0 & W \\ \end{bmatrix} \] 其中\(W\)是一個列向量,可以拆開 \[\begin{bmatrix} w_1 & 0 \\ w_2 & 0 \\ 0 & w_1 \\ 0 & w_2 \\ \end{bmatrix} \]
總結及思考
- 交叉網路最終輸出是什麼?需要推導看一下和多項式的區別以及每個特徵的引數?
- \(X_0X_l^T\)的一階性質是秩為1嗎?為什麼會導致無需計算和儲存整個矩陣?
- 多項式近似的理論證明?為什麼需要的引數量少?
- 引數共享思想?FM和DCN到底怎麼實現的引數共享?
- 高效對映高效體現在哪裡?複雜度是\(O(d)\)嗎?
