Lisp之根源 --- 保羅格雷厄姆
Lisp之根源 --- 保羅格雷厄姆
來源 http://daiyuwen.freeshell.org/gb/rol/roots_of_lisp.html
約翰麥卡錫於1960年發表了一篇非凡的論文,他在這篇論文中對程式設計的貢獻有如 歐幾里德對幾何的貢獻.1 他向我們展示了,在只給定幾個簡單的操作符和一個 表示函式的記號的基礎上, 如何構造出一個完整的程式語言. 麥卡錫稱這種語 言為Lisp, 意為List Processing, 因為他的主要思想之一是用一種簡單的資料 結構表(list)來代表程式碼和資料.
值得注意的是,麥卡錫所作的發現,不僅是計算機史上劃時代的大事, 而且是一種 在我們這個時代程式設計越來越趨向的模式.我認為目前為止只有兩種真正乾淨利落, 始終如一的程式設計模式:C語言模式和Lisp語言模式.此二者就象兩座高地, 在它們 中間是尤如沼澤的低地.隨著計算機變得越來越強大,新開發的語言一直在堅定地 趨向於Lisp模式. 二十年來,開發新程式語言的一個流行的祕決是,取C語言的計 算模式,逐漸地往上加Lisp模式的特性,例如執行時型別和無用單元收集.
在這篇文章中我儘可能用最簡單的術語來解釋約翰麥卡錫所做的發現. 關鍵是我 們不僅要學習某個人四十年前得出的有趣理論結果, 而且展示程式語言的發展方 向. Lisp的不同尋常之處--也就是它優質的定義--是它能夠自己來編寫自己. 為了理解約翰麥卡錫所表述的這個特點,我們將追溯他的步伐,並將他的數學標記 轉換成能夠執行的Common Lisp程式碼.
七個原始操作符
開始我們先定義表示式.表示式或是一個原子(atom),它是一個字母序列(如 foo),或是一個由零個或多個表示式組成的表(list), 表示式之間用空格分開, 放入一對括號中. 以下是一些表示式:
foo () (foo) (foo bar) (a b (c) d)
最後一個表示式是由四個元素組成的表, 第三個元素本身是由一個元素組成的表.
在算術中表達式 1 + 1 得出值2. 正確的Lisp表示式也有值. 如果表示式e得出 值v,我們說e返回v. 下一步我們將定義幾種表示式以及它們的返回值.
如果一個表示式是表,我們稱第一個元素為操作符,其餘的元素為自變數.我們將 定義七個原始(從公理的意義上說)操作符: quote,atom,eq,car,cdr,cons,和 cond.
- (quote x) 返回x.為了可讀性我們把(quote x)簡記 為'x.
> (quote a) a > 'a a > (quote (a b c)) (a b c)
- (atom x)返回原子t如果x的值是一個原子或是空表,否則返回(). 在Lisp中我們 按慣例用原子t表示真, 而用空表表示假.
> (atom 'a) t > (atom '(a b c)) () > (atom '()) t
既然有了一個自變數需要求值的操作符, 我們可以看一下quote的作用. 通過引 用(quote)一個表,我們避免它被求值. 一個未被引用的表作為自變數傳給象 atom這樣的操作符將被視為程式碼:
> (atom (atom 'a)) t
反之一個被引用的表僅被視為表, 在此例中就是有兩個元素的表:
> (atom '(atom 'a)) ()
這與我們在英語中使用引號的方式一致. Cambridge(劍橋)是一個位於麻薩諸塞 州有90000人口的城鎮. 而``Cambridge''是一個由9個字母組成的單詞.
引用看上去可能有點奇怪因為極少有其它語言有類似的概念. 它和Lisp最與眾 不同的特徵緊密聯絡:程式碼和資料由相同的資料結構構成, 而我們用quote操作符 來區分它們.
- (eq x y)返回t如果x和y的值是同一個原子或都是空表, 否則返回().
> (eq 'a 'a) t > (eq 'a 'b) () > (eq '() '()) t
- (car x)期望x的值是一個表並且返回x的第一個元素.
> (car '(a b c)) a
- (cdr x)期望x的值是一個表並且返回x的第一個元素之後的所有元素.
> (cdr '(a b c)) (b c)
- (cons x y)期望y的值是一個表並且返回一個新表,它的第一個元素是x的值, 後 面跟著y的值的各個元素.
> (cons 'a '(b c)) (a b c) > (cons 'a (cons 'b (cons 'c '()))) (a b c) > (car (cons 'a '(b c))) a > (cdr (cons 'a '(b c))) (b c)
- (cond (
...
) ...(
...
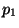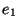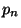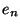)) 的求值規則如下. p表示式依次求值直到有一個 返回t. 如果能找到這樣的p表示式,相應的e表示式的值作為整個cond表示式的 返回值. > (cond ((eq 'a 'b) 'first) ((atom 'a) 'second)) second當表示式以七個原始操作符中的五個開頭時,它的自變數總是要求值的.2 我們稱這樣 的操作符為函式.
函式的表示
接著我們定義一個記號來描述函式.函式表示為(lambda (...) e),其中 ...是原子(叫做引數),e是表示式. 如果表示式的第一個元素形式如 上
((lambda (...) e) 
...
)
則稱為函式呼叫.它的值計算如下.每一個表示式
先求值,然後e再求值.在e的 求值過程中,每個出現在e中的
的值是相應的在最近一 次的函式呼叫中的值.
> ((lambda (x) (cons x '(b))) 'a) (a b) > ((lambda (x y) (cons x (cdr y))) 'z '(a b c)) (z b c)
如果一個表示式的第一個元素f是原子且f不是原始操作符
(f ...)
並且f的值是一個函式(lambda (...)),則以上表達式的值就是
((lambda (...) e) ...)
的值. 換句話說,引數在表示式中不但可以作為自變數也可以作為操作符使用:
> ((lambda (f) (f '(b c))) '(lambda (x) (cons 'a x))) (a b c)
有另外一個函式記號使得函式能提及它本身,這樣我們就能方便地定義遞迴函 數.3 記號
(label f (lambda (...) e))
表示一個象(lambda (...) e)那樣的函式,加上這樣的特性: 任何出現在e中的f將求值為此label表示式, 就好象f是此函式的引數.
假設我們要定義函式(subst x y z), 它取表示式x,原子y和表z做引數,返回一個 象z那樣的表, 不過z中出現的y(在任何巢狀層次上)被x代替.
> (subst 'm 'b '(a b (a b c) d)) (a m (a m c) d)
我們可以這樣表示此函式
(label subst (lambda (x y z)
(cond ((atom z)
(cond ((eq z y) x)
('t z)))
('t (cons (subst x y (car z))
(subst x y (cdr z)))))))
我們簡記f=(label f (lambda (...) e))為
(defun f (...) e)
於是
(defun subst (x y z)
(cond ((atom z)
(cond ((eq z y) x)
('t z)))
('t (cons (subst x y (car z))
(subst x y (cdr z))))))
偶然地我們在這兒看到如何寫cond表示式的預設子句. 第一個元素是't的子句總 是會成功的. 於是
(cond (x y) ('t z))
等同於我們在某些語言中寫的
if x then y else z
一些函式
既然我們有了表示函式的方法,我們根據七個原始操作符來定義一些新的函式. 為了方便我們引進一些常見模式的簡記法. 我們用cxr,其中x是a或d的序列,來 簡記相應的car和cdr的組合. 比如(cadr e)是(car (cdr e))的簡記,它返回e的 第二個元素.
> (cadr '((a b) (c d) e)) (c d) > (caddr '((a b) (c d) e)) e > (cdar '((a b) (c d) e)) (b)
我們還用(list ...)表示(cons ...(cons '()) ...).
> (cons 'a (cons 'b (cons 'c '()))) (a b c) > (list 'a 'b 'c) (a b c)
現在我們定義一些新函式. 我在函式名後面加了點,以區別函式和定義它們的原 始函式,也避免與現存的common Lisp的函式衝突.
- (null. x)測試它的自變數是否是空表.
(defun null. (x) (eq x '())) > (null. 'a) () > (null. '()) t
- (and. x y)返回t如果它的兩個自變數都是t, 否則返回().
(defun and. (x y) (cond (x (cond (y 't) ('t '()))) ('t '()))) > (and. (atom 'a) (eq 'a 'a)) t > (and. (atom 'a) (eq 'a 'b)) () - (not. x)返回t如果它的自變數返回(),返回()如果它的自變數返回t.
(defun not. (x) (cond (x '()) ('t 't))) > (not. (eq 'a 'a)) () > (not. (eq 'a 'b)) t - (append. x y)取兩個表並返回它們的連結.
(defun append. (x y) (cond ((null. x) y) ('t (cons (car x) (append. (cdr x) y))))) > (append. '(a b) '(c d)) (a b c d) > (append. '() '(c d)) (c d) - (pair. x y)取兩個相同長度的表,返回一個由雙元素表構成的表,雙元素表是相 應位置的x,y的元素對.
(defun pair. (x y) (cond ((and. (null. x) (null. y)) '()) ((and. (not. (atom x)) (not. (atom y))) (cons (list (car x) (car y)) (pair. (cdr) (cdr y)))))) > (pair. '(x y z) '(a b c)) ((x a) (y b) (z c)) - (assoc. x y)取原子x和形如pair.函式所返回的表y,返回y中第一個符合如下條 件的表的第二個元素:它的第一個元素是x.
(defun assoc. (x y) (cond ((eq (caar y) x) (cadar y)) ('t (assoc. x (cdr y))))) > (assoc. 'x '((x a) (y b))) a > (assoc. 'x '((x new) (x a) (y b))) new
一個驚喜
因此我們能夠定義函式來連線表,替換表示式等等.也許算是一個優美的表示法, 那下一步呢? 現在驚喜來了. 我們可以寫一個函式作為我們語言的直譯器:此函 數取任意Lisp表示式作自變數並返回它的值. 如下所示:
(defun eval. (e a)
(cond
((atom e) (assoc. e a))
((atom (car e))
(cond
((eq (car e) 'quote) (cadr e))
((eq (car e) 'atom) (atom (eval. (cadr e) a)))
((eq (car e) 'eq) (eq (eval. (cadr e) a)
(eval. (caddr e) a)))
((eq (car e) 'car) (car (eval. (cadr e) a)))
((eq (car e) 'cdr) (cdr (eval. (cadr e) a)))
((eq (car e) 'cons) (cons (eval. (cadr e) a)
(eval. (caddr e) a)))
((eq (car e) 'cond) (evcon. (cdr e) a))
('t (eval. (cons (assoc. (car e) a)
(cdr e))
a))))
((eq (caar e) 'label)
(eval. (cons (caddar e) (cdr e))
(cons (list (cadar e) (car e)) a)))
((eq (caar e) 'lambda)
(eval. (caddar e)
(append. (pair. (cadar e) (evlis. (cdr e) a))
a)))))
(defun evcon. (c a)
(cond ((eval. (caar c) a)
(eval. (cadar c) a))
('t (evcon. (cdr c) a))))
(defun evlis. (m a)
(cond ((null. m) '())
('t (cons (eval. (car m) a)
(evlis. (cdr m) a)))))
eval.的定義比我們以前看到的都要長. 讓我們考慮它的每一部分是如何工作的.
eval.有兩個自變數: e是要求值的表示式, a是由一些賦給原子的值構成的表,這 些值有點象函式呼叫中的引數. 這個形如pair.的返回值的表叫做環境. 正是 為了構造和搜尋這種表我們才寫了pair.和assoc..
eval.的骨架是一個有四個子句的cond表示式. 如何對錶達式求值取決於它的類 型. 第一個子句處理原子. 如果e是原子, 我們在環境中尋找它的值:
> (eval. 'x '((x a) (y b))) a
第二個子句是另一個cond, 它處理形如(a ...)的表示式, 其中a是原子. 這包 括所有的原始操作符, 每個對應一條子句.
> (eval. '(eq 'a 'a) '())
t
> (eval. '(cons x '(b c))
'((x a) (y b)))
(a b c)
這幾個子句(除了quote)都呼叫eval.來尋找自變數的值.
最後兩個子句更復雜些. 為了求cond表示式的值我們呼叫了一個叫 evcon.的輔助函式. 它遞迴地對cond子句進行求值,尋找第一個元素返回t的子句. 如果找到 了這樣的子句, 它返回此子句的第二個元素.
> (eval. '(cond ((atom x) 'atom)
('t 'list))
'((x '(a b))))
list
第二個子句的最後部分處理函式呼叫. 它把原子替換為它的值(應該是lambda 或label表示式)然後對所得結果表示式求值. 於是
(eval. '(f '(b c))
'((f (lambda (x) (cons 'a x)))))
變為
(eval. '((lambda (x) (cons 'a x)) '(b c))
'((f (lambda (x) (cons 'a x)))))
它返回(a b c).
eval.的最後cond兩個子句處理第一個元素是lambda或label的函式呼叫.為了對label 表示式求值, 先把函式名和函式本身壓入環境, 然後呼叫eval.對一個內部有 lambda的表示式求值. 即:
(eval. '((label firstatom (lambda (x)
(cond ((atom x) x)
('t (firstatom (car x))))))
y)
'((y ((a b) (c d)))))
變為
(eval. '((lambda (x)
(cond ((atom x) x)
('t (firstatom (car x)))))
y)
'((firstatom
(label firstatom (lambda (x)
(cond ((atom x) x)
('t (firstatom (car x)))))))
(y ((a b) (c d)))))
最終返回a.
最後,對形如((lambda (...) e) ...)的表示式求值,先呼叫evlis.來 求得自變數(...)對應的值(
...
),把()...()新增到 環境裡, 然後對e求值. 於是
(eval. '((lambda (x y) (cons x (cdr y)))
'a
'(b c d))
'())
變為
(eval. '(cons x (cdr y))
'((x a) (y (b c d))))
最終返回(a c d).
後果
既然理解了eval是如何工作的, 讓我們回過頭考慮一下這意味著什麼. 我們在這 兒得到了一個非常優美的計算模型. 僅用quote,atom,eq,car,cdr,cons,和cond, 我們定義了函式eval.,它事實上實現了我們的語言,用它可以定義任何我們想要 的額外的函式.
當然早已有了各種計算模型--最著名的是圖靈機. 但是圖靈機程式難以讀懂. 如果你要一種描述演算法的語言, 你可能需要更抽象的, 而這就是約翰麥卡錫定義 Lisp的目標之一.
約翰麥卡錫於1960年定義的語言還缺不少東西. 它沒有副作用, 沒有連續執行 (它得和副作用在一起才有用), 沒有實際可用的數,4 沒有動態可視域. 但這些限制可 以令人驚訝地用極少的額外程式碼來補救. Steele和Sussman在一篇叫做``直譯器 的藝術''的著名論文中描述瞭如何做到這點.5
如果你理解了約翰麥卡錫的eval, 那你就不僅僅是理解了程式語言歷史中的一個 階段. 這些思想至今仍是Lisp的語義核心. 所以從某種意義上, 學習約翰麥卡 錫的原著向我們展示了Lisp究竟是什麼. 與其說Lisp是麥卡錫的設計,不如說是 他的發現. 它不是生來就是一門用於人工智慧, 快速原型開發或同等層次任務的 語言. 它是你試圖公理化計算的結果(之一).
隨著時間的推移, 中級語言, 即被中間層程式設計師使用的語言, 正一致地向Lisp靠 近. 因此通過理解eval你正在明白將來的主流計算模式會是什麼樣.
註釋
把約翰麥卡錫的記號翻譯為程式碼的過程中我儘可能地少做改動. 我有過讓程式碼 更容易閱讀的念頭, 但是我還是想保持原汁原味.
在約翰麥卡錫的論文中,假用f來表示, 而不是空表. 我用空表表示假以使例子能 在Common Lisp中執行. (fixme)
我略過了構造dotted pairs, 因為你不需要它來理解eval. 我也沒有提apply, 雖然是apply(它的早期形式, 主要作用是引用自變數), 被約翰麥卡錫在1960年 稱為普遍函式, eval只是不過是被apply呼叫的子程式來完成所有的工作.
我定義了list和cxr等作為簡記法因為麥卡錫就是這麼做的. 實際上 cxr等可以 被定義為普通的函式. List也可以這樣, 如果我們修改eval, 這很容易做到, 讓 函式可以接受任意數目的自變數.
麥卡錫的論文中只有五個原始操作符. 他使用了cond和quote,但可能把它們作 為他的元語言的一部分. 同樣他也沒有定義邏輯操作符and和not, 這不是個問題, 因為它們可以被定義成合適的函式.
在eval.的定義中我們呼叫了其它函式如pair.和assoc.,但任何我們用原始操作 符定義的函式呼叫都可以用eval.來代替. 即
(assoc. (car e) a)
能寫成
(eval. '((label assoc.
(lambda (x y)
(cond ((eq (caar y) x) (cadar y))
('t (assoc. x (cdr y))))))
(car e)
a)
(cons (list 'e e) (cons (list 'a a) a)))
麥卡錫的eval有一個錯誤. 第16行是(相當於)(evlis. (cdr e) a)而不是(cdr e), 這使得自變數在一個有名函式的呼叫中被求值兩次. 這顯示當論文發表的 時候, eval的這種描述還沒有用IBM 704機器語言實現. 它還證明了如果不去運 行程式, 要保證不管多短的程式的正確性是多麼困難.
我還在麥卡錫的論文中碰到一個問題. 在定義了eval之後, 他繼續給出了一些 更高階的函式--接受其它函式作為自變數的函式. 他定義了maplist:
(label maplist
(lambda (x f)
(cond ((null x) '())
('t (cons (f x) (maplist (cdr x) f))))))
然後用它寫了一個做微分的簡單函式diff. 但是diff傳給maplist一個用x做參 數的函式, 對它的引用被maplist中的引數x所捕獲.6
這是關於動態可視域危險性的雄辯證據, 即使是最早的更高階函式的例子也因為 它而出錯. 可能麥卡錫在1960年還沒有充分意識到動態可視域的含意. 動態可 視域令人驚異地在Lisp實現中存在了相當長的時間--直到Sussman和Steele於 1975年開發了Scheme. 詞法可視域沒使eval的定義複雜多少, 卻使編譯器更難 寫了.
About this document ...
Lisp之根源
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split=0 roots_of_lisp.tex
The translation was initiated by Dai Yuwen on 2003-10-24
Footnotes
- ... 歐幾里德對幾何的貢獻. 1
- ``Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part1.'' Communication of the ACM 3:4, April 1960, pp. 184-195.
- ...當表示式以七個原始操作符中的五個開頭時,它的自變數總是要求值的. 2
- 以另外兩個操作符quote和cond開頭的表示式以不同的方式求值. 當 quote表示式求值時, 它的自變數不被求值,而是作為整個表示式的值返回. 在 一個正確的cond表示式中, 只有L形路徑上的子表示式會被求值.
- ... 數. 3
- 邏輯上我們不需要為了這定義一個新的記號. 在現有的記號中用 一個叫做Y組合器的函式上的函式, 我們可以定義遞迴函式. 可能麥卡錫在寫 這篇論文的時候還不知道Y組合器; 無論如何, label可讀性更強.
- ... 沒有實際可用的數, 4
- 在麥卡錫的1960 年的Lisp中, 做算術是可能的, 比如用一個有n個原子的表表示數n.
- ... 的藝術''的著名論文中描述瞭如何做到這點. 5
- Guy Lewis Steele, Jr. and Gerald Jay Sussman, ``The Art of the Interpreter, or the Modularity Complex(Parts Zero,One,and Two),'' MIT AL Lab Memo 453, May 1978.
- ... 對它的引用被maplist中的引數x所捕獲. 6
- 當代的Lisp程式 員在這兒會用mapcar代替maplist. 這個例子解開了一個謎團: maplist為什 麼會在Common Lisp中. 它是最早的對映函式, mapcar是後來增加的.
Dai Yuwen 2003-10-24 ============== End