同一空間參考體系中大地問題的解算

當採用某一橢球體（參考橢球）來描述地球時，橢球面則作為計算的基準面，計算地面點的空間位置。那麼，橢球面的橢球要素（點，線，面）的幾何特徵（座標，長度，面積）又該怎麼計算呢？

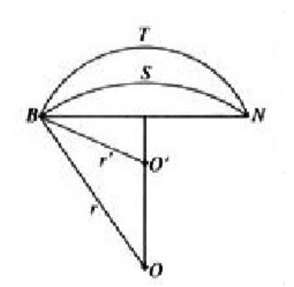
##曲面上幾何要素的定義 ###大圓，大圓弧 如圖，O為球體的幾何中心，OB為球體半徑。顯然在垂直BN，過O的旋轉軸上，可以以旋轉軸上的點為圓心（如O´），以圓心到B的距離為半徑（O´B）作很多個圓弧，但是隻有以OB為半徑作的圓為大圓，S為大圓弧。

###法線，法截線 曲面上某一點的法線指的是經過這一點並且與該點切平面垂直的那條直線（即向量）。

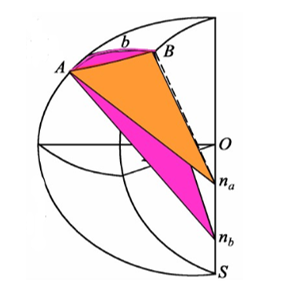
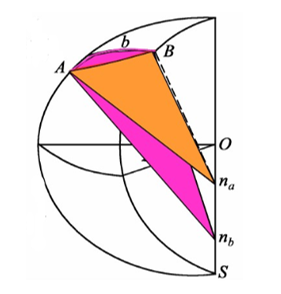
如圖，由於過A，B點所作的法線不交於一點（na,nb），A到B就可以得到兩條法截線。由橢球面上A點的法線與B點所確定的法截面與橢球面相割得到的曲線稱為A到B的法截線，橢球面上B點的法線與A點所確定的法截面與橢球面相割得到的曲線稱為B到A的法截線。

###卯酉圈 過橢球面上一點的法線，可作無線多個法截面，其中一個與該點子午線相垂直的法截面，與橢球面相截形成的閉合圈，稱為卯酉圈。

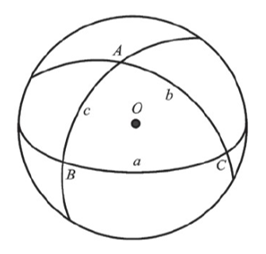
###球面三角形，球面角，球面角超 構成球面三角形的大圓弧稱為三角形的頂點，過球面三角形頂點分別作大圓弧的切線，兩條切線所成的角稱為球面三角形的角，顯然球面三角形的三個內角之和大於180度，大於180度部分我們稱為球面角超。如圖，圖一ABC則為球面三角形，圖二角B´AC´即為球面角。

在這裡插入圖片描述

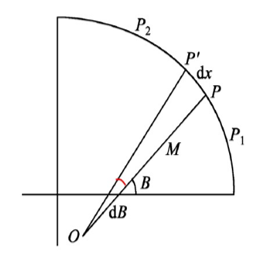
##橢球問題的解算內容 ###弧長 在球面上，弧長可由其所在的圓內，有簡單的弧長計算公式得到。而在橢球體面，我們需要通過微積分進行解算。

###測地線（大地線，短程線）長度 ####測地線的概念 在曲面上，連線兩點的最短路徑我們稱為測地線。

我們知道在二維平面上兩點之間線段最短，但在橢球面上，我們定義的座標是經緯度，我們無法穿透橢球以尋求最短距離。橢球上，起點和終點的連線可以有千萬條路徑，哪一條又是最短呢？

在球面上，連線兩點之間的最短距離是經過這兩點的一段大圓弧弧長。

在橢球面上，過橢球面的起點和終點可以得到兩條法截線，在兩條法截線之間取一條相對法截線，使兩點的距離最短，那麼，這條相對法截線就是測地線。而測地線和法截線的差異甚微，當長度達到600km，二者差異僅為0.007mm。通常，我們用法截線代替橢球面的測地線。

####測地線的使用 （1）已知地球表面任意兩個點的位置（B，L），我們可以求取這兩點間的測地線長度。

（2）已知地球表面的若干個點，同樣，我們可以求取通過這些點的連續測地線長度。

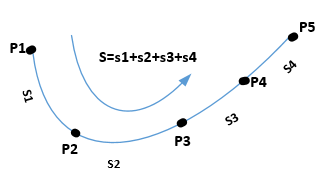
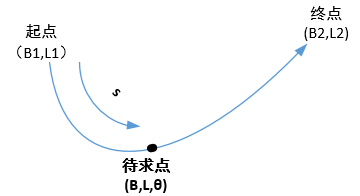
（3）由已知起點的位置（B1，L1），我們可以沿著特定的方向（方位角），經過一定的測地線距離，到達終點的位置（B2，L2）。

（4）在經過起點和終點的測地線上，我們可以求取沿該測地線任意一小段距離對應的點座標（B，L）。

測地線的使用具有重要的現實意義。比如，在飛機航飛，航空攝影，輪渡，鐵路修建的過程中，為了節省燃料，建材等資源，沿著測地線進行分段定點，不斷調整航向，使整個過程中，經過的直線距離總和近似地和測地線長度相等。

####測地線的計算 根據起終點的經緯度和方位角，法截線的計算可由卯酉圈曲率半徑，以及兩點間的角差進行解算。

其中，A為大地方位角，北方向為0度，順時針旋轉。

在精度允許的情況下，我們也可以採用球面上大圓弧弧長代替測地線的長度。

更為精密的大地線計算方式可由大地線微分方程和克萊姆方程，進行微積分解算。

###曲面周長和空間面積 在球面上，已知三角形的三個角的大小和三點的座標，分別求每一條弧線的長度，三條弧線之和即為周長，面積按照下式計算。

在橢球面上，曲面多邊形的邊長對應為測地線長度，內角為球面角。

如果為曲面多邊形，則對構成多邊形的曲線進行分割，按照微積分的方式進行計算，標準積分面積逆時針方向的點返回正面積，反向則計算得負面積。