P2144 [FJOI2007]輪狀病毒

題目描述

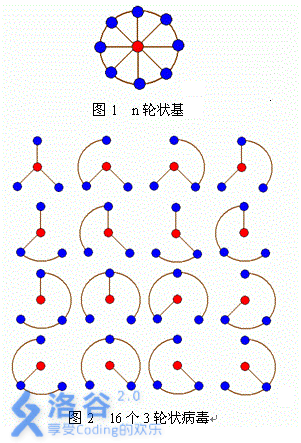
輪狀病毒有很多變種。許多輪狀病毒都是由一個輪狀基產生。一個\(n\)輪狀基由圓環上\(n\)個不同的基原子和圓心的一個核原子構成。\(2\)個原子之間的邊表示這\(2\)個原子之間的資訊通道，如圖\(1\)。

\(n\)輪狀病毒的產生規律是在\(n\)輪狀基中刪除若干邊，使各原子之間有唯一一條資訊通道。例如，共有\(16\)個不同的\(3\)輪狀病毒，如圖\(2\)所示。

給定\(n(n\le100)\)，程式設計計算有多少個不同的\(n\)輪狀病毒。

輸入輸出格式

輸入格式：

第一行有\(1\)個正整數\(n\)。

輸出格式：

將程式設計計算出的不同的\(n\)

發現題目要求求出看起來很有規律的無向圖生成樹個數，顯然可以找一些規律/打表/遞推之類的，但不妨採用比較暴力的方法，矩陣樹定理。

然後發現事情並沒有那麼簡單，如果用矩陣樹定理暴力去做的話，你可以選擇一些亂搞/手寫高精度小數類之類的方法

而之前又說，這個圖比較特殊，所以，我們可以研究一下基爾霍夫矩陣的行列式有沒有什麼比較特殊的求法，\(n+1(n>2)\)階的基爾霍夫矩陣大概長這個樣子

\[\begin{bmatrix}n&-1&-1&-1&-1&\cdots&-1&-1&-1\\-1&3&-1&0&0&\cdots&0&0&-1\\-1&-1&3&-1&0&\dots&0&0&0\\-1&0&-1&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\-1&0&0&0&0&\cdots&-1&3&-1\\-1&-1&0&0&0&\cdots&0&-1&3\end{bmatrix}\]

\(n\)階主子式肯定是扔第一行第一列啊，因為我們想找行列式的遞推規律，然後變成這樣

\[\begin{bmatrix}3&-1&0&0&\cdots&0&0&-1\\-1&3&-1&0&\dots&0&0&0\\0&-1&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&0&\cdots&-1&3&-1\\-1&0&0&0&\cdots&0&-1&3\end{bmatrix}\]

設這個矩陣為\(A_n\)，那麼\(n\)的答案就是\(\det A_n\)，然後我們考慮求出這個矩陣的行列式

由“行列式等於它的任一行（列）的各元素與其對應的代數餘子式乘積之和”

• 餘子式：在\(n\)階行列式中，把元素\(a_{i,j}\)所在第\(i\)行和第\(j\)行劃去後，留下的\(n-1\)階行列式叫元素\(a_{i,j}\)的餘子式，記做\(M_{i,j}\)，定義代數餘子式為\(A_{i,j}=(-1)^{i+j}M_{i,j}\)

我們可以扔第一行，因為\((1,n)\)和\((n,1)\)兩個位置的東西看起來巨難受。

拆開第一行第一列得到

\[3\begin{vmatrix}3&-1&0&\dots&0&0&0\\-1&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&\cdots&-1&3&-1\\0&0&0&\cdots&0&-1&3\end{vmatrix}\]

這個看起來就可以遞推的東西，設\(n-1\)階的它為\(B_{n-1}\)。為了方便，以下\(A_n,B_n\)也指代行列式的值。

然後剩下有貢獻的第一行第二列和第一行第\(n-1\)列，因為餘子式的正負與\(n\)有關，不妨先設\(n\)為奇數，偶數的情況是一樣的。

\[\begin{vmatrix}-1&-1&0&\dots&0&0&0\\0&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&\cdots&-1&3&-1\\-1&0&0&\cdots&0&-1&3\end{vmatrix}\]

這是拆了第一行第二列，沒思路再拆，發現扔第一行第一列後是\(-B_{n-2}\)，扔第\(n-1\)行第\(1\)列是主對角線全為\(-1\)的下三角，行列式的值為\(-1\)，再乘上\((-1)^{n-1+1}(-1)\)還是\(-1\)

然後是第一行第\(n\)列

\[-\begin{vmatrix}-1&3&-1&0&\dots&0&0\\0&-1&3&-1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&-1&3\\-1&0&0&0&\cdots&0&-1\end{vmatrix}\]

注意這裡是負的，因為\(n\)是奇數。然後還是拆第一列，發現答案還是\(-B_{n-2}\)和\(-1\)

於是我們有\(A_n=3B_{n-1}-2B_{n-2}-2\)

以同樣的方法對\(B\)做討論，可以得到\(B_n=3B_{n-1}-B_{n-2}\)

然後聯立一下得到\(A_{n}=3A_{n-1}-A_{n-2}+2\)，帶入到\(n\le2\)發現式子仍然成立，然後直接遞推+高精即可。

Code:

#include <cstdio>
#include <cstring>
const int N=110;
struct bignum
{
    int num[N];
    bignum(){memset(num,0,sizeof(num));}
    bignum friend operator +(bignum n1,bignum n2)
    {
        int len=n1.num[0]>n2.num[0]?n1.num[0]:n2.num[0];
        for(int i=1;i<=len;i++)
        {
            n1.num[i]+=n2.num[i];
            n1.num[i+1]+=n1.num[i]/10;
            n1.num[i]%=10;
        }
        if(n1.num[len+1]) n1.num[0]=len+1;
        else n1.num[0]=len;
        return n1;
    }
    bignum friend operator -(bignum n1,bignum n2)
    {
        int len=n1.num[0];
        for(int i=1;i<=len;i++)
        {
            n1.num[i]-=n2.num[i];
            if(n1.num[i]<0)
                n1.num[i]+=10,n1.num[i+1]--;
        }
        if(n1.num[len]) n1.num[0]=len;
        else n1.num[0]=len-1;
        return n1;
    }
}ans[N],two;
int main()
{
    int n;scanf("%d",&n);
    ans[1].num[0]=1,ans[1].num[1]=1,ans[2].num[0]=1,ans[2].num[1]=5,two.num[0]=1,two.num[1]=2;
    for(int i=3;i<=n;i++) ans[i]=ans[i-1]+ans[i-1]+ans[i-1]-ans[i-2]+two;
    for(int i=ans[n].num[0];i;i--) printf("%d",ans[n].num[i]);
    return 0;
}

2018.12.20