單源最短路徑問題是：對於給定的有向網路G=（V，E）及單個源點v，求v到G的其餘各頂點的最短路徑。

演算法的基本思想

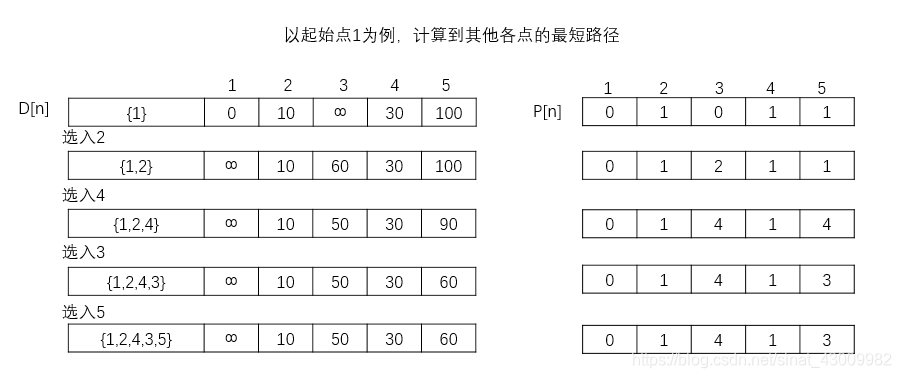
a.初始時，S只包含源點，即S＝{v}，v的距離為0。U包含除v外的其他頂點，即:U={其餘頂點}，若v與U中頂點u有邊，則<u,v>正常有權值，若u不是v的出邊鄰接點，則<u,v>權值為∞。

b.從U中選取一個距離v最小的頂點k，把k，加入S中（該選定的距離就是v到k的最短路徑長度）。

c.以k為新考慮的中間點，修改U中各頂點的距離；若從源點v到頂點u的距離（經過頂點k）比原來距離（不經過頂點k）短，則修改頂點u的距離值，修改後的距離值的頂點k的距離加上邊上的權。

d.重複步驟b和c直到所有頂點都包含在S中。

演算法程式碼

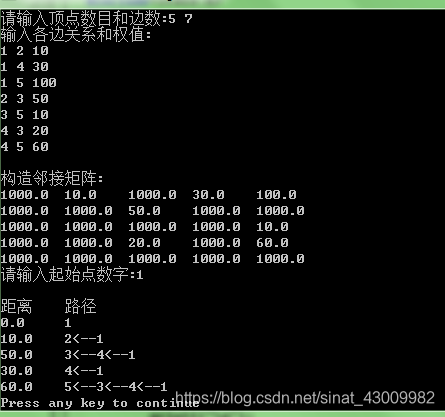
#include<stdio.h>
#define max 1000                        //1000定義為最大值正無窮，表示兩點之間不直接相通，或與自己相連線。
#define n 100                           //n表示一個範圍，需要大於圖的頂點數目，以便定義一個數組儲存。n的具體值根據情況而定。
main()
{
	void DIJ(float C[n][n],int v);
	int i,j,k,e,r;
	float z;
	float a[n][n];                       //定義一個足夠大的陣列，用於儲存圖的資料。
	for(i=0;i<n;i++)
	for(j=0;j<n;j++)
	{
		a[i][j]=max;                      //在正式寫入資料之前，定義任意兩點之間是不連通的，以便在後面為連通的資料單獨賦值。
	}
	printf("請輸入頂點數目和邊數:");      //明確圖中的節點數目和之間的邊數。
	scanf("%d%d",&r,&e);
	printf("輸入各邊關係和權值:\n");
	for(k=0;k<e;k++)                      //輸入各邊之間的連線點與權值。如1,2點之間的距離是10，應該輸入“1 2 10”。
	{
		scanf("%d%d%f",&i,&j,&z);
		a[i-1][j-1]=z;                    //只建立有向圖用這句
	}
	printf("\n構造鄰接矩陣:");
	for(i=0;i<r;i++)                       //把圖用鄰接矩陣的形式輸出。
	{
		printf("\n");
		for(j=0;j<r;j++)
		{
			printf("%.1f\t",a[i][j]);
		}
	}
	printf("\n");
	printf("請輸入起始點數字:");           //輸入需要從某個節點開始。
	scanf("%d",&i);
	printf("\n距離\t路徑");
	DIJ(a,i);
}
void DIJ(float C[n][n],int v)                //Dijkstra演算法
{
	float D[n];                              //用於儲存起始點到其他各點間的距離
	int P[n],S[n];                           //P[n]用陣列儲存當前點的前驅結點，S[n]表示已經取過的點集，代表紅點集。
	int i,j,k,v1,pre;
	float min,inf=200;                       //inf一定要大於所有點間路徑最大的數，這樣才保證距離最大值的點能擴充到已經取好的點
	v1=v-1;
	for(i=0;i<n;i++)                        
	{
		D[i]=C[v1][i];                       //置初始距離值
		if(D[i]!=max)                        //初始狀態下各前驅結點。
			P[i]=v;
		else P[i]=0;                         //如果兩點非連線定義其前驅為0
	}
	for(i=0;i<n;i++)                          
		S[i]=0;                              //紅點集開始是空集
	S[v1]=1;                                 //初始點入紅點集
	D[v1]=0;                                 //設定初始點到自身的距離為0
	for(i=0;i<n-1;i++)                       //擴充紅點集
	{
		min=inf;                              
		for(j=0;j<n;j++)                     
			if((!S[j])&&(D[j]<min))
			{
				min=D[j];
				k=j;
			}
			S[k]=1;							//在當前藍點集中選取距離最小的頂點k+1，並加入紅點集
			for(j=0;j<n;j++)
				if((!S[j])&&(D[j]>D[k]+C[k][j]))//調整各藍點的間距值
				{
					D[j]=D[k]+C[k][j];         //修改藍點j+1到紅點集的距離
					P[j]=k+1;                  //改變j+1的前驅為k+1
				}
	}										//所有頂點都擴充到S中
	for(i=0;i<n;i++)
	{
		if(D[i]!=max)
		printf("\n%.1f\t%d",D[i],i+1);        //列印兩點間能連通的結果
		pre=P[i];
		while(pre!=0)							//用於繼續找前驅結點
		{
			printf("<--%d",pre);
			pre=P[pre-1];
		}
	}
	printf("\n");
}

 

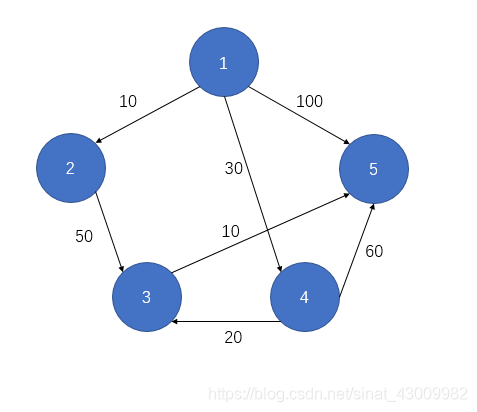
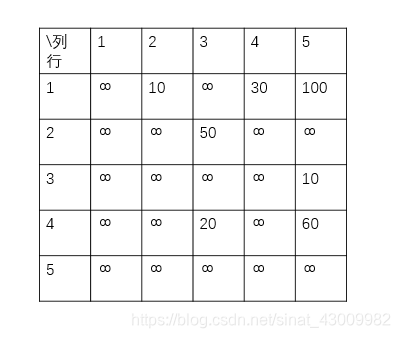
以下圖有向網路為例 其鄰接矩陣為 先舉個例子，求1到其它各點的最短路徑。 具體分析步驟如下圖 最後一行就是求得的結果。 1->1=0。 1->2=10:看最後一行，到達2的前驅是1。則輸出1->2。 1->3=50:到達3的前驅是4，到達4的前驅是1。則輸出1->4->3。 1->4=30:到達4的前驅是1。則輸出1->4。 1->5=60:到達5的前驅是3，到達3的前驅是4，到達4的前驅是1。則依次輸出1->4->3->5。 程式輸出結果如下