梯度下降是機器學習常用的優化方法之一，用來求解無約束目標函式(損失函式)的極值。但是它收斂到的是區域性最小值，當函式是凸函式時，可以收斂到全域性最小值。當我們在模型中運用梯度下降法求解時，其實就是求解在該模型損失函式取得最小值時所對用的模型引數值是多少。當然梯度下降也可以單純的用來求解一個函式的極值。

梯度是函式值上升變化最快的方向，可以求得函式的最大值；所以負梯度就是函式值下降變化最快的方向，可以求得函式的最小值。因為梯度指引的只是一個方向，具體要變化多少就需要步長，也就是學習率。下面是梯度下降演算法的描述：

資料集為D = {(x1, y1), (x2, y2),......, (xm, ym)},

初始化引數：模型需要求得的引數                                                           

           迭代更新引數, 其中 i  為迭代的次數，alpha為學習率，為所有樣本的損失：

當損失函式的值小於一個閾值時，就停止迭代。

在這裡舉一個簡單的線性迴歸，利用梯度下降求解模型引數的?：

線性迴歸的假設函式為, 其中θ0和θ1就是模型的引數；：

損失函式為 ：

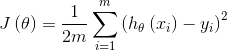
初始化θ0 ，θ1= 0；

將所有的樣本帶入到損失函式中，然後分別對θ0和θ1求導，並更新θ0和θ1：

直到的值小於一個閾值，則停止迭代

在搜尋極值的過程中，學習率大小的選擇很重要。

學習率太小，函式值下降收斂的速度就很慢；

           學習率太大，收斂的過程就會出現震盪，還有可能最終不能收斂。