題目描述

【問題描述】 Hanks 博士是BT (Bio-Tech，生物技術) 領域的知名專家，他的兒子名叫Hankson。現 在，剛剛放學回家的Hankson 正在思考一個有趣的問題。 今天在課堂上，老師講解了如何求兩個正整數c1 和c2 的最大公約數和最小公倍數。現 在Hankson 認為自己已經熟練地掌握了這些知識，他開始思考一個“求公約數”和“求公 倍數”之類問題的“逆問題”，這個問題是這樣的：已知正整數a0,a1,b0,b1，設某未知正整 數x 滿足： 1． x 和a0 的最大公約數是a1； 2． x 和b0 的最小公倍數是b1。 Hankson 的“逆問題”就是求出滿足條件的正整數x。但稍加思索之後，他發現這樣的 x 並不唯一，甚至可能不存在。因此他轉而開始考慮如何求解滿足條件的x 的個數。請你幫 助他程式設計求解這個問題。 【輸入】 輸入檔名為 son.in。第一行為一個正整數n，表示有n 組輸入資料。接下來的n 行每 行一組輸入資料，為四個正整數a0，a1，b0，b1，每兩個整數之間用一個空格隔開。輸入 資料保證a0 能被a1 整除，b1 能被b0 整除。 【輸出】 輸出檔案 son.out 共n 行。每組輸入資料的輸出結果佔一行，為一個整數。 對於每組資料：若不存在這樣的 x，請輸出0； 若存在這樣的 x，請輸出滿足條件的x 的個數；

題解：

由題得 ：

gcd( x , a0)=a1

x*b0/gcd(x,b0)=b1;

這樣不好看 

x=p*a1;   p=x/a1

a0=q*a1;  q=a0/a1

我們猜測 p,q的關係 ：gcd(p,q)==1

設 gcd(p,q)=K != 1

p=k*n

q=k*m

所以 x=k*n*a1,a0=k*m*a1

顯然 gcd(x,a0)=K*a1 不成立

可以推廣結論:

gcd(x,y)=k 則有 gcd(x/k,y/k)=1

這樣就很明朗了

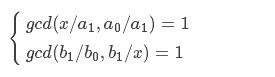
列舉b1的因子記數就行了

#include<cstdio>
#include<cstring>
#include<algorithm>
typedef long long ll;
using namespace std;
int a0,a1,b0,b1;
int cas,ans;
int gcd(int a,int b){
	return a==0?b:gcd(b%a,a); 
}
int main(){
//	freopen("p1072.in","r",stdin);
	scanf("%d",&cas);
	while(cas--){
		scanf("%d%d%d%d",&a0,&a1,&b0,&b1);
		ans=0;int p=a0/a1;int q=b1/b0;
		for(int x=1;x*x<=b1;x++ ){
			if(b1%x==0){
				if(x%a1==0 && gcd(x/a1,p)==1 && gcd(b1/x,q)==1) ans++;
				int y=b1/x;if(y==x) continue;
				if(y%a1==0 && gcd(y/a1,p)==1 && gcd(b1/y,q)==1) ans++;
			}
		}
		printf("%d\n",ans);
	}
	
	
	return 0;
}