在引入時間序列前，先介紹幾個matlab函式

matlab中的gallery函式簡析

Matlab 中的 gallery 函式是一個測試矩陣生成函式。當我們需要對某些演算法進行測試的時候，可以利用gallery函式來生成各種性質的測試矩陣。其用法如下：
[A,B,C,…] =gallery(matname,P1,P2,…,classname)
其中matname表示矩陣性質，classname表示矩陣元素是single還是double
例如：

x=gallery('uniformdata',[1 10],0)
>>x =
  1 至 7 列
    0.9501    0.2311    0.6068    0.4860    0.8913    0.7621    0.4565
  8 至 10 列
    0.0185    0.8214    0.4447
y = gallery('uniformdata',[1 10],1)
>>y =
  1 至 7 列
    0.9528    0.7041    0.9539    0.5982    0.8407    0.4428    0.8368
  8 至 10 列
    0.5187    0.0222    0.3759
 

其中 uniformdata 表示均勻分佈，[1 10] 表示x是一個長度為10的陣列，最後一個引數 0和1表示不同的矩陣，如果反覆引用x=gallery(‘uniformdata’,[1 10],0)，那麼得到的陣列總是相同的。
下面我們按照測試矩陣生成的點畫出來

x=gallery('uniformdata',[1 10],0)；
y = gallery('uniformdata',[1 10],1)；
plot(x,y,'o')
hold on
voronoi(x,y)

如下圖所示：

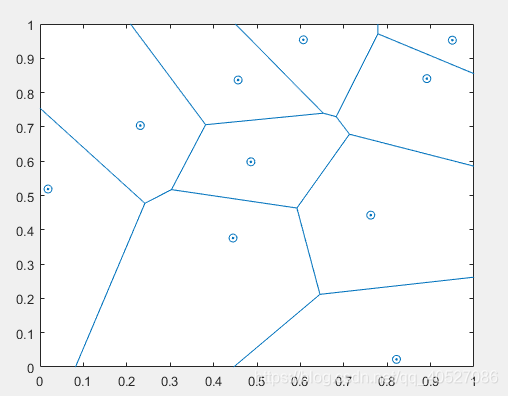
其中，中心點為按照某種模式生成的點。邊框為voronoi diagram

模擬時間序列分析

介紹了剛才的gallery函式，下面基於其模擬的時間序列數值進行相關操作。

模擬

建立一個模擬資料集並計算其平均值。假設 sdata表示股票的每日價格變化。

t = 0:200;
dailyFluct = gallery('normaldata',size(t),2);
sdata = cumsum(dailyFluct) + 20 + t/100;
%計算均值
mean_data = mean(sdata)

畫出來生成的模擬資料大概長成這樣，我們假設橫座標為時間，縱座標為股票價格。從模擬函式sdata = cumsum(dailyFluct) + 20 + t/100和圖看來資料是具有趨勢性的。

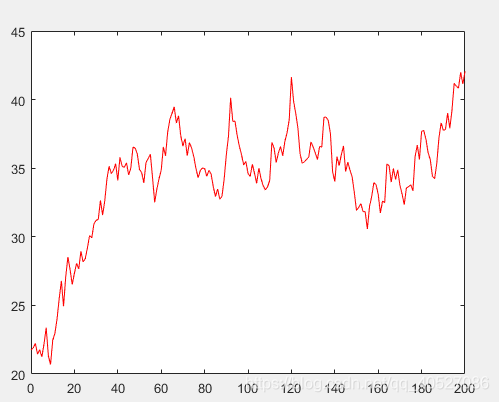
去趨勢

目的：去趨勢（detrend）處理可以消除感測器在獲取資料時產生的偏移對後期計算產生的影響。從資料中刪除趨勢可以將分析集中在資料趨勢本身的波動上。但是，去趨勢的意義取決於自己的研究的目的。

方法：資料去趨勢，就是對資料減去一條最優（最小二乘）的擬合直線、平面或曲面，使去趨勢後的資料均值為零。

在matlab中，可以使用detrend函式去除時間序列x中的均值或線性趨勢，這在FFT處理中尤其常用。
格式引數如下：

y = detrend(x) % 消除時間序列中的線性趨勢項
y = detrend(x,'constant') % 消除時間序列中的均值
y = detrend(x,'linear',bp) % 分段消除時間序列中的線性趨勢項,bp為分段點向量

例如如：

sig = [0 1 -2 1 0 1 -2 1 0]; % 無線性趨勢的訊號
trend = [0 1 2 3 4 3 2 1 0]; % 有兩段線性的趨勢
x = sig+trend; % 將上面趨勢疊加到訊號上
y = detrend(x,'linear',5) % 根據指定的分段點去除兩段線性趨勢

我們對上述資料進行去趨勢處理如下：

%計算去趨勢資料，並且從原始資料中移除
detrend_sdata = detrend(sdata);
trend = sdata - detrend_sdata;
mean(detrend_sdata)

最後，我們繪圖如下：

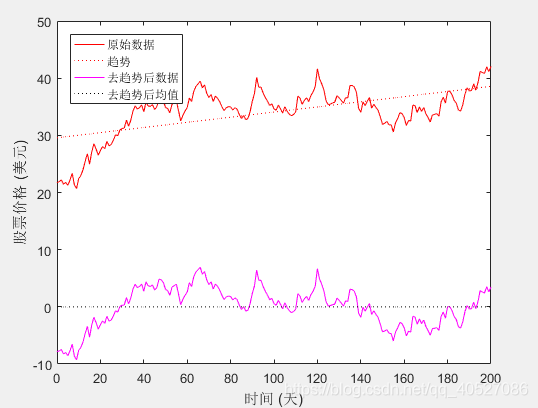
完整程式碼：

t = 0:200;
dailyFluct = gallery('normaldata',size(t),2);
sdata = cumsum(dailyFluct) + 20 + t/100;
%計算均值
mean_data = mean(sdata);
figure(1)
plot(t,sdata,'r')
legend('Original Data','Location','northwest');
xlabel('Time (days)');
ylabel('Stock Price (dollars)');
%計算去趨勢資料，並且從原始資料中移除
detrend_sdata = detrend(sdata);
%原資料減去去趨勢後的資料就是趨勢項了
trend = sdata - detrend_sdata;
%計算去趨勢後的均值，發現極小接近於0
mean(detrend_sdata)

hold on
plot(t,trend,':r')
plot(t,detrend_sdata,'m')
plot(t,zeros(size(t)),':k')
legend('原始資料','趨勢','去趨勢後資料',...
       '去趨勢後均值','Location','northwest')
xlabel('時間 (天)');

一個具體的案例 --移動開戶數分析

我們有一份移動公司兩年間共計700余天的每日開戶樹，我們想探尋其中的隨機因素。

去趨勢項和去季節項

繪製原開戶資料的變化趨勢如下：

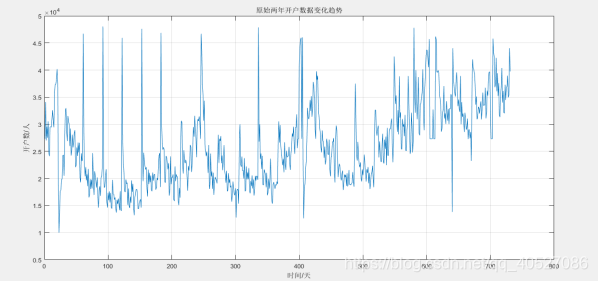
圖一.原開戶資料趨勢變化的觀察

可以發現，開戶數在區域性區間的極值變化具有一定的週期性。但是資料太多且有點雜亂。
為了更好的觀察資料的規律，擬將資料進行滑動平均處理，在一定程度上更能看出規律性。並且，依據兩年的月數天數變化，設定標記每月天數變化的向量，計算每月，每個季度，每年的平均開戶數進行觀察。計算並繪製得到下圖：

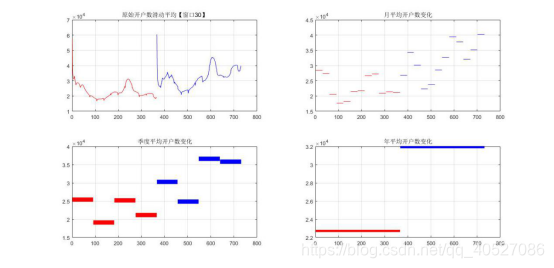
圖二.開戶資料趨勢變化週期的觀察

上圖紅色標記為2012年，藍色標記為2013年。總的看來均有上升的趨勢。圖二左上角繪製的是2012和2013的開戶數滑動平均觀察（使用matlab smooth函式，滑動視窗設定為30），容易發現在年這個層面上趨勢具有較大的相關性，一年顯然可以是一個大週期的刻畫。但是這個週期太大了，如果選取這個週期做去季節性，顯然會損失大量資料。因此，我們想找到一個更小的週期來刻畫，其實我們還可以發現圖一中有明顯的小起伏，經驗證起伏平均間隔為30即一個月，那麼一個月是否為一個週期呢？右上圖是按月進行平均的統計值繪製，起伏貌似沒有什麼規律。但是還是可以作為參考。左下角圖繪製的是季度的平均開戶數變化，可以發現兩個季度為一個週期，因為起伏在兩個週期中進行。右下角圖繪製的是年平均變化圖，如我們所料，隨著移動網際網路的普及，2013年開戶平均數比2012年高。

綜上觀察，我們可以得出以下結論：
1.一個月應該是一個最小週期，兩個季度是一箇中週期，一年為一個確定的大週期。
2.開戶人數有明顯的上升趨勢。
3.由觀測值我們可以認為存在異常值。

2.資料的預處理
2.1缺失值處理
資料中不存在缺失值
2.2異常值處理
擬採用三倍標準差即拉以達法則篩選異常值，考慮到時間序列的短期影響性，用其周圍值平均代替。

3.平穩化–去趨勢與去週期
進行了簡單的觀察和資料預處理後，我們開始正式進行時間序列平穩化的操作。考慮到有兩年，我們從單獨考慮2012，2013，然後集中考慮2012和2013來進行處理和檢驗。
3.1去趨勢
由於資料變化有一定的集中性，且有滑動平均看來近似可以用一次函式擬合。所以採用一次差分的方法去除資料的趨勢項。這裡採用diff函式實現一次差分。去趨勢後，我們進行了如下的觀察：

圖三.週期為一個月的檢驗圖
我們發現相鄰極值點間的時間差距十分接近於一個月，這讓我們欣喜萬分。

3.2去週期
由以上的觀察資料和去趨勢後資料綜合考慮，採用一個月作為週期是個不錯的選擇。這裡自定義d步差分函式對去趨勢後的資料進行去週期的處理。
經過3.1和3.2,我們得到如下結果：

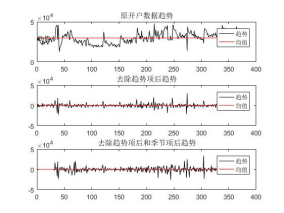
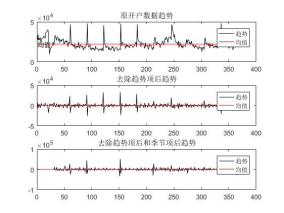
圖四.2012年去趨勢和去週期比較圖 圖五.2013年去趨勢和去週期比較圖

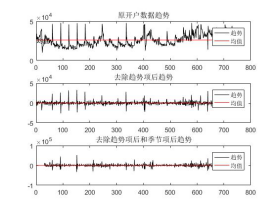
圖六.2012-2013年去趨勢和去週期比較圖

肉眼看來，效果還算不錯，從均值線看來均值均十分接近於0。為了更客觀的看待平穩的效果，採用自相關圖還進行平穩性的驗證。

自相關性平穩性檢驗結果如下：

圖七.自相關圖檢驗平穩性
從自相關圖看來，經過去趨勢和去週期後的資料的確是平穩的。 經過以上步驟，我們就成功的將非平穩的時間序列轉換為了平穩的時間序列，得到了隨機誤差項的表示。