摘要：本文討論如何使用一個簡單的演算法計算一個大整數n的階乘，大數採用char陣列儲存，一個元素表示1位10進位制數。本中給出一個完整的計算大數階乘的程式,該程式在迅馳1.7G筆記本上計算10000的階乘大約2.7秒。
 
    在《大數階乘之計算從入門到精通－大數的表示》中，我們學習瞭如何表示和儲存一個大數。在這篇文章中，我們將討論如何對大數做乘法運算，並給出一個可以求出一個整數n的階乘的所有有效數字的程式。大整數的儲存和表示已經在上一篇文章做了詳細的介紹。其中最簡單的表示法是:大數用一個字元型陣列來表示，陣列的每一個元素表示一位十進位制數字，高位在前，低位在後。那麼，用這種表示法，如何做乘法運算呢？其實這個問題並不困難，可以使用模擬手算的方法來實現。回憶一下我們在小學時，是如何做一位數乘以多位數的乘法運算的。例如：2234*8。
  
 
我們將被乘數表示為一個數組A[], a[1],a[2],a[3],a[4]分別為2,2,3,4,a[0]置為0。
Step1: 從被乘數的個位a[4]起，取出一個數字4.
Step2: 與乘數8相乘，其積是兩位數32，其個位數2作為結果的個位,存入a[4], 十位數3存入進位c。
Step3: 取被乘數的上一位數字a[3]與乘數相乘，並加上上一步計算過程的進位C,得到27，將這個數的個位7作為結果的倒數第二位，存入a[3]，十位數2存入進位c。
Step4：重複Step3,取a[i]（i依次為4,3,2,1）與乘數相乘並加上c,其個位仍存入a[i],　十位數字存入c，直到i等於1為止。
Step5:將最後一步的進位c作為積的最高位a[0]。
 
這一過程其實和小學學過的多位數乘以一位數的珠算乘法一模一樣，學過珠算乘法的朋友還有印象嗎？
 
在計算大數階乘的過程中，乘數一般不是一位數字，那麼如何計算呢？我們可以稍作變通，將上次的進位加上本次的積得到數P,　將P除以10的餘數做為結果的本位，將P除以10的商作為進位。當被乘數的所有數字都和乘數相乘完畢後，將進位C放在積的最前面即可。下面給出C語言程式碼。
一個m位數乘以n位數，其結果為m+n-1,或者m+n位，所以需首先定義一個至少m+n個元素的陣列，並置前n位為0。
 
計算一個m位的被乘數乘以一個n位的整數k，積仍儲存於陣列a

void mul(unsigned char a[],unsigned long k,int m,int n)
{
	int i;
	unsigned long p;
	unsigned long c=0;
	
	for ( i=m+n-1; i>=n;i--)
	{
		p= a[i] * k +c;
		a[i]=(unsigned char)( p % 10);
		c= p / 10;
	}
	
	while (c>0)
	{
		a[i]=(unsigned char)( c % 10);
		i--;
		c /=10;
	}
}
 
int main(int argc, char* argv[])
{
	int i;
	unsigned char a[]={0,0,0,2,3,4,5};
	mul(a,678,4,3);
	i=0;
	while ( a[i]==0)
		i++;
	for (;i<4+3;i++)
		printf("%c",a[i]+’0’); //由於數a[i]（0<=a[i] <=9）對應的可列印字任符為’0’到’9’,所以顯示為i＋’0’ 
	return 0;
}

從上面的例子可知，在做乘法之前，必須為陣列保留足夠的空間。具體到計算n!的階乘時，必須準備一個能容納的n!的所有位數的陣列或者記憶體塊。即陣列採有靜態分配或者動態分配。前者程式碼簡潔，但只適應於n小於一個固定的值，後者靈活性強，只要有足夠的記憶體，可計算任意n的階乘，我們這裡討論後一種情況，如何分配一塊大小合適的記憶體。

n!有多少位數呢？我們給出一個近似的上限值：n!<(n+12)nn!<(n+12)n，下面是推導過程。
Caes 1: n是奇數，則中間的那個數m=(n+1)/2, 除了這個數外，我們可以將1到n之間的數分成n/2組，每組的兩個數為 m-i 和m+i (i=1到m-1),如1,2,3,4,5,6,7 可以分為數4，和3對數，它們是(3,5),(2,6)和(1,7),容易知道，每對數的積都於小 m2m2，故 n!<mn=(n+12)nn!<mn=(n+12)n的次方。
 
 
     Case 2: n 是個偶數，則中間的兩個數(n/2)和(n/2+1),其它的幾對兒數是(n/2-1,n/2+2),(n/2-2,n/2+3)等等。容易證明，這幾對兒數中，中間的那對數n/2和n/2+1的乘積最大，因為共有n/2對數，故
    n!<(n2(n2+1))n/2=(n2+2n4)n2<((n+12)2)n2=(n+12)nn!<(n2(n2+1))n/2=(n2+2n4)n2<((n+12)2)n2=(n+12)n

     由以上兩種情況可知，對於任意大於1的正整數n, n!<(n+12)nn!<(n+12)n。如果想求出n!更準確的上限，可以使用司特林公式，參見該系列文章《階乘之計算從入門到精通－近似計算之二》。
 
到此，我們已經解決大數階乘之計算的主要難題，到了該寫出一個完整程式的時候了，下面給出一個完整的程式碼。

程式執行

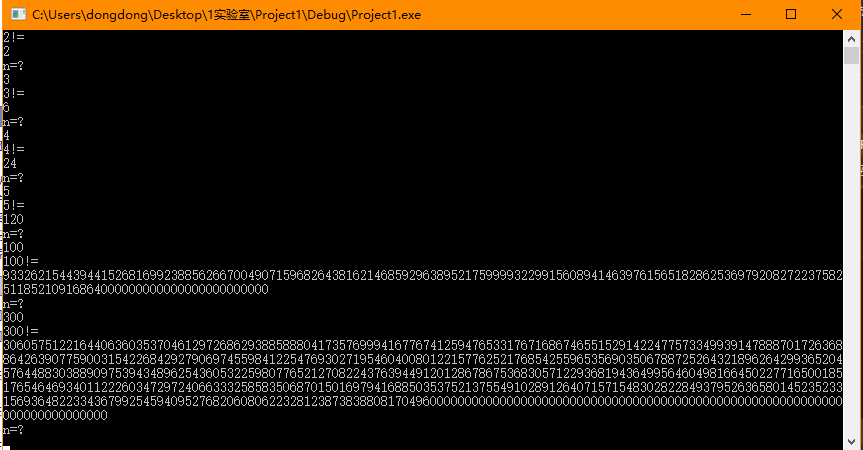
新建一個VS工程

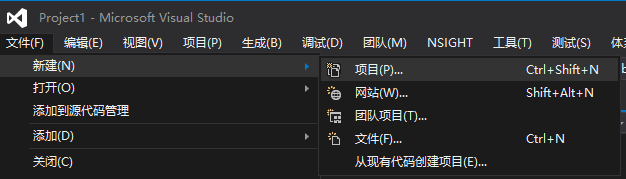
選擇空專案

新增一個cpp檔案

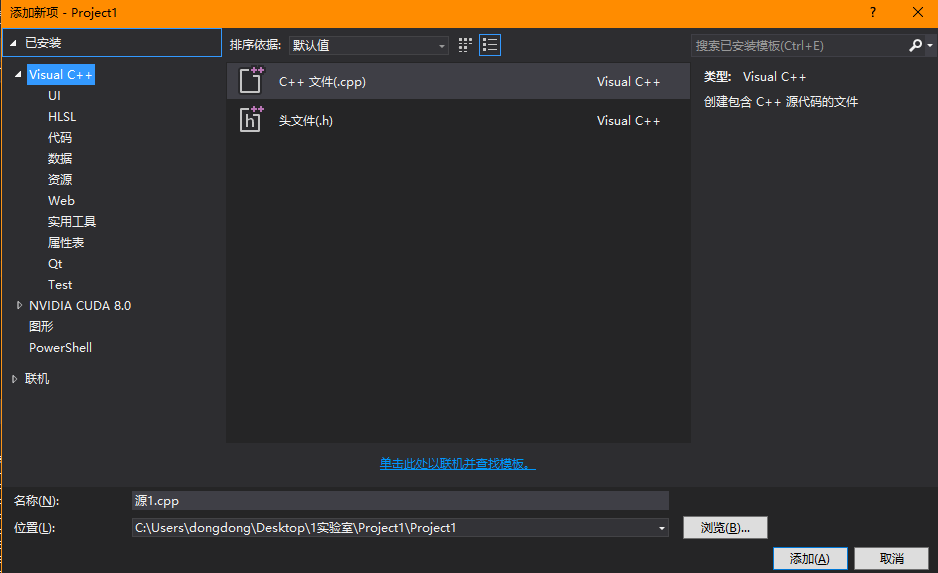
把程式碼貼進去

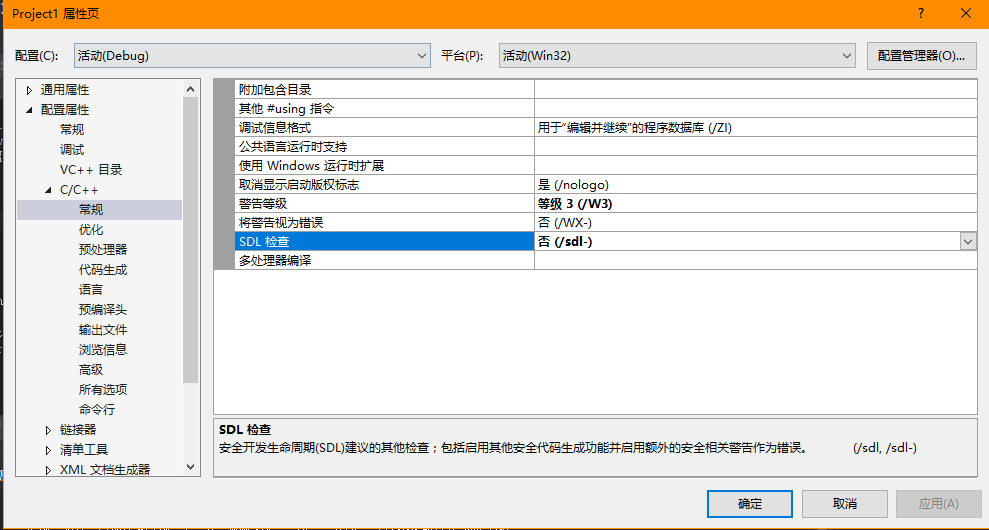
遇到 scanf（）函式報錯問題

右鍵專案-屬性

圖示選否

#include "stdio.h" 
#include "stdlib.h" 
#include "memory.h" 
#include "math.h" 
#include "malloc.h" 

void calcFac(unsigned long n)
{
	unsigned long i, j, head, tail;
	int blkLen = (int)(n*log10(double(n + 1) / 2)); //計算n!有數數字的個數 
	blkLen += 4;  //保險起見，多加4位 

	if (n <= 1)
	{
		printf("%d!=0\n", n);     return;
	}

	char *arr = (char *)malloc(blkLen);
	if (arr == NULL)
	{
		printf("alloc memory fail\n"); return;
	}

	memset(arr, 0, sizeof(char)*blkLen);
	head = tail = blkLen - 1;
	arr[tail] = 1;

	for (i = 2; i <= n; i++)
	{
		unsigned long c = 0;
		for (j = tail; j >= head; j--)
		{
			unsigned long prod = arr[j] * i + c;
			arr[j] = (char)(prod % 10);
			c = prod / 10;
		}
		while (c>0)
		{
			head--;
			arr[head] = (char)(c % 10);
			c /= 10;
		}
	}
	printf("%d!=\n", n);
	for (i = head; i <= tail; i++)
		printf("%c", arr[i] + '0');
	printf("\n");

	free(arr);
}

void testCalcFac()
{
	int n;
	while (1)
	{
		printf("n=?\n");
		scanf("%ld", &n);
		if (n == 0)
			break;
		calcFac(n);
	}
}

int main(int argc, char* argv[])
{
	testCalcFac();
	return 0;
}