Android翻頁效果原理實現之曲線的實現
尊重原創轉載請註明:From AigeStudio(http://blog.csdn.net/aigestudio)Power by Aige 侵權必究!
炮兵
上一節我們通過引入折線實現了頁面的摺疊翻轉效果,有了前面兩節的基礎呢其實曲線的實現可以變得非常簡單,為什麼這麼說呢?因為曲線無非就是在折線的基礎上對Path加入了曲線的實現,進而只是影響了我們的Region區域,而其他的什麼事件啊、滑動計算啊之類的幾乎都是不變的對吧,說白了就是對現有的折線View進行update改造,雖然是改造,但是我們該如何下手呢?首先我們來看看現實中翻頁的效果應該是怎樣的呢?如果大家身邊有書或本子甚至一張紙也行,嘗試以不同的方式去翻動它,你會發現除了我們前面兩節曾提到過的一些限制外,還有一些special的現象:
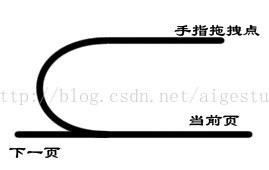
一、翻起來的區域從側面來看是一個有弧度的區域,如圖所示側面圖:
而我們將按照第一節中的約定忽略這部分弧度的表現,因為從正俯視的角度我們壓根看不到弧度的效果,So~我們強制讓其與頁面平行:
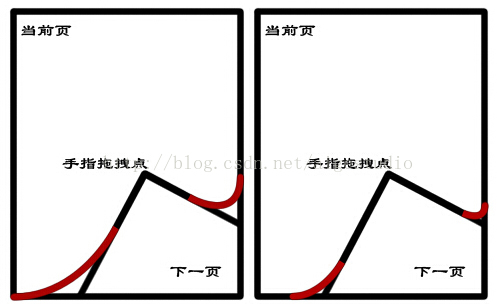
二、根據拖拽點距離頁面高度的不同,我們可以得到不同的捲曲度:
而其在我們正俯視點的表現則是曲線的弧度不同:
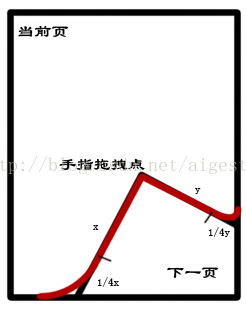
同樣的,我們按照第一節的約定,為了簡化問題,我們將拖拽點距離頁面的高度視為一個定值使在我們正俯視點表現的曲線起點從距離控制元件交點1/4處開始:
三、如上一節末所說,在彎曲的區域影象也會有相似的扭曲效果
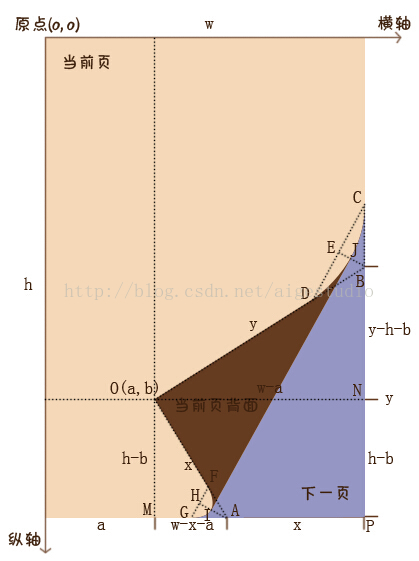
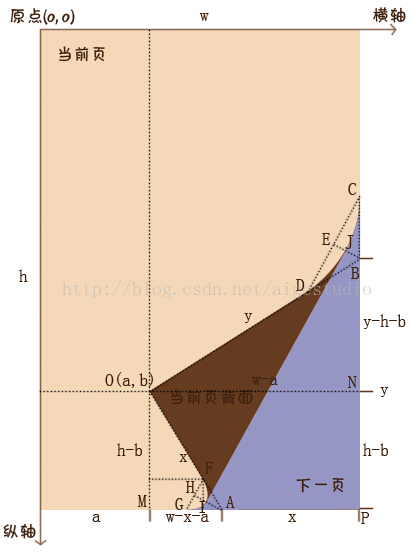
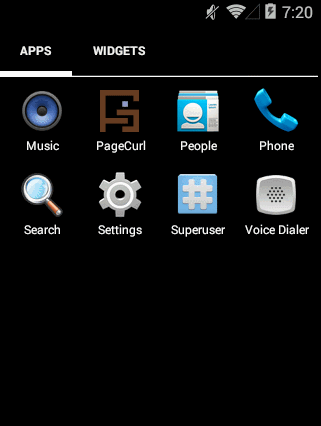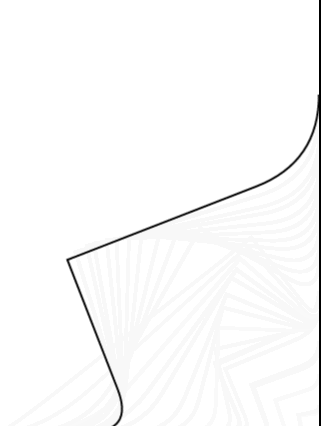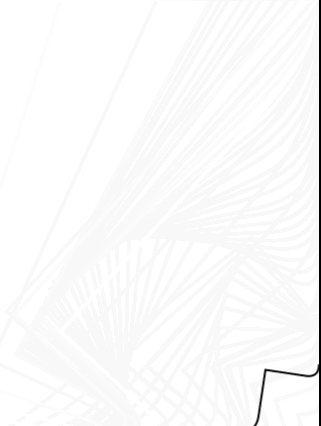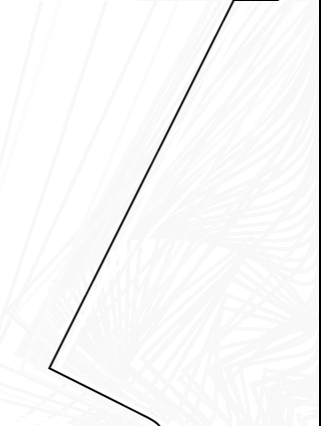
OK,大致的一個分析就是這樣,我們根據分析結果可以得出下面的一個分析圖:
由上圖配合我們上面的分析我們可知:DB = 1/4OB,FA = 1/4OA,而點F和點D分別為兩條曲線(如無特殊宣告,我們所說的曲線均為貝賽爾曲線,下同)的起點(當然你也可以說是終點無所謂),這時,我們以點A、B為曲線的控制點並以其為端點分別沿著x軸和y軸方向作線段AG、BC,另AG = AF、BC = BD,並令點G、C分別為曲線的終點,這樣,我們的這兩條二階貝塞爾曲線就非常非常的特殊,例如上圖中的曲線DC,它是由起始點D、C和控制點B構成,而BD = BC,也就是說三角形BDC是的等腰三角形,進一步地說就是曲線DC的兩條控制桿力臂相等,進一步地我們可以推斷出曲線DC的頂點J必定在直線DC的中垂線上,更進一步地我們可以根據《自定義控制元件其實很簡單5/12》所說的二階貝塞爾曲線公式得出當且僅當t = 0.5時曲線的端點剛好會在頂點J上,由此我們可以非常非常簡單地得到曲線的頂點座標。好了,YY歸YY我們還是要回歸到具體的操作中來,首先,我們要計算出點G、F、D、C的座標值,這四點座標也相當easy,就拿F點座標來說,我們過點F分別作OM、AM的垂線:
因為FA = 1/4OA,那麼我們可以得到F點的x座標Fx = a + 3/4MA,y座標Fy = b + 3/4OM,而G點的x座標Gx = a + MA - 1/4x;其他兩點D、C就不多扯了,那麼在程式碼中如何體現呢?首先,為了便於觀察效果,我們先註釋掉圖片的繪製:
/* * 如果座標點在原點(即還沒發生觸碰時)則繪製第一頁 */if (mPointX == 0 && mPointY == 0) { // canvas.drawBitmap(mBitmaps.get(mBitmaps.size() - 1), 0, 0, null); return;}// 省略大量程式碼//drawBitmaps(canvas); canvas.drawPath(mPath, mPaint);if (sizeLong > mViewHeight) { //…………………………} else { //…………………………}// 計算曲線起點float startXBtm = btmX2 - CURVATURE * sizeShort;float startYBtm = mViewHeight;// 計算曲線終點float endXBtm = mPointX + (1 - CURVATURE) * (tempAM);float endYBtm = mPointY + (1 - CURVATURE) * mL;// 計算曲線控制點float controlXBtm = btmX2;float controlYBtm = mViewHeight;// 計算曲線頂點float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm;float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm;/* * 生成帶曲線的四邊形路徑 */mPath.moveTo(startXBtm, startYBtm);mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);mPath.lineTo(mPointX, mPointY);mPath.lineTo(topX1, 0);mPath.lineTo(topX2, 0);mPath.lineTo(bezierPeakXBtm, bezierPeakYBtm);PS:為了便於大家對引數的理解,我對每一個點的座標都重新給予了一個引用其命名也淺顯易懂,實際過程可以省略這一步簡化程式碼
而當sizeLong <= mViewHeight時這時候不但底部有曲線效果,右側也有:
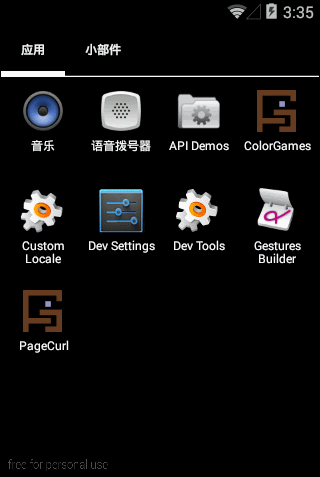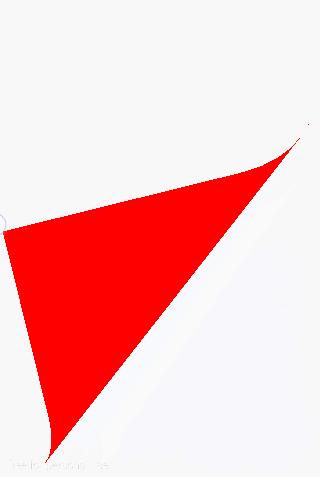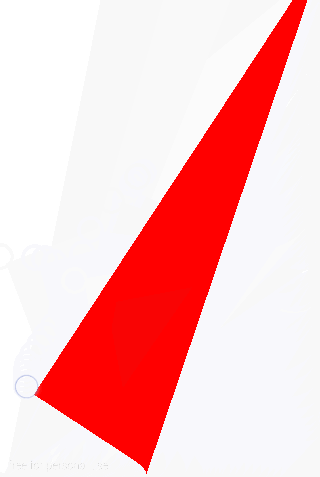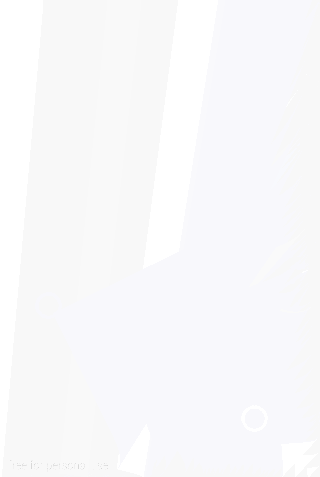
/* * 計算引數 */float leftY = mViewHeight - sizeLong;float btmX = mViewWidth - sizeShort;// 計算曲線起點float startXBtm = btmX - CURVATURE * sizeShort;float startYBtm = mViewHeight;float startXLeft = mViewWidth;float startYLeft = leftY - CURVATURE * sizeLong;/* * 限制左側曲線起點 */if (startYLeft <= 0) { startYLeft = 0;}/* * 限制右側曲線起點 */if (startXBtm <= 0) { startXBtm = 0;}// 計算曲線終點float endXBtm = mPointX + (1 - CURVATURE) * (tempAM);float endYBtm = mPointY + (1 - CURVATURE) * mL;float endXLeft = mPointX + (1 - CURVATURE) * mK;float endYLeft = mPointY - (1 - CURVATURE) * (sizeLong - mL);// 計算曲線控制點float controlXBtm = btmX;float controlYBtm = mViewHeight;float controlXLeft = mViewWidth;float controlYLeft = leftY;// 計算曲線頂點float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm;float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm;float bezierPeakXLeft = 0.25F * startXLeft + 0.5F * controlXLeft + 0.25F * endXLeft;float bezierPeakYLeft = 0.25F * startYLeft + 0.5F * controlYLeft + 0.25F * endYLeft;/* * 生成帶曲線的三角形路徑 */mPath.moveTo(startXBtm, startYBtm);mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);mPath.lineTo(mPointX, mPointY);mPath.lineTo(endXLeft, endYLeft);mPath.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft);Path有了,我們就該考慮如何將其轉換為Region,在這個過程中呢又一個問題,曲線路徑不像上一節的直線路徑我們可以輕易獲得其範圍區域,因為我們的摺疊區域其實應該是這樣的:
如圖所示紅色路徑區域,這部分割槽域則是我們摺疊的區域,而事實上我們為了計算方便將整條二階貝賽爾曲線都繪製了出來,也就是說我們的Path除了紅色線條部分還包含了藍色線條部分對吧,那麼問題來了,如何將這兩部分“做掉”呢?其實方法很多,我們可以在計算的時候就只生成半條曲線,這是方法一我們利用純計算的方式,記得我在該系列文章開頭曾說過翻頁效果的實現可以有兩種方式,一種是純計算而另一種則是利用圖形的組合思想,如何組合呢?這裡對於區域的計算我們就不用純計算的方式了,我們嘗試用圖形組合來試試。首先我們將Path轉為Region看看是什麼樣的:
Region region = computeRegion(mPath);canvas.clipRegion(region);canvas.drawColor(Color.RED);// canvas.drawPath(mPath, mPaint);可以看到我們沒有封閉的Path形成的Region效果,事實呢跟我們需要的區域差距有點大,首先上下兩個月半圓是多餘的,其次目測少了一塊對吧:
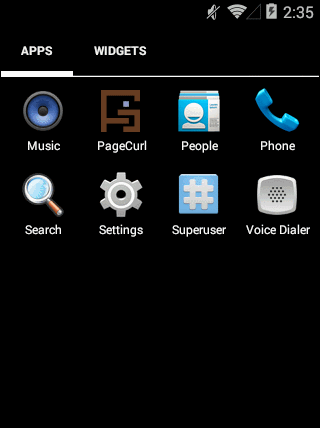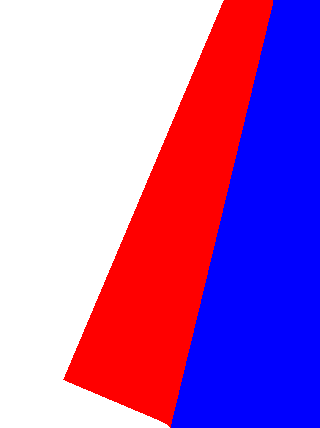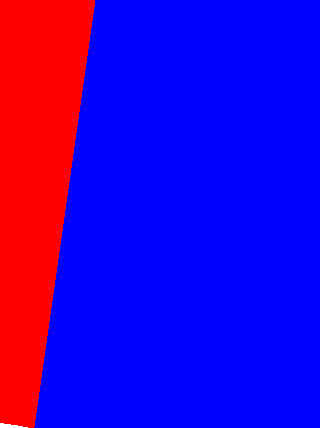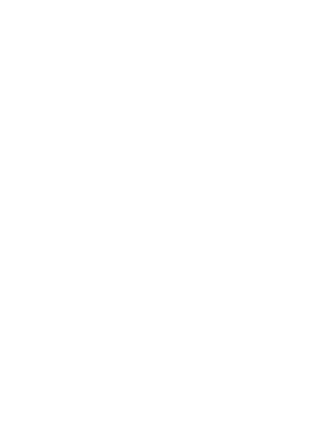
如上圖藍色的那塊,那麼我們該如何把這塊“補”回來呢?利用圖形組合的思想,我們設法為該Region補一塊矩形:
然後差集掉兩個月半圓不就成了?這部分程式碼改動較大,我先貼程式碼再說吧:
if (sizeLong > mViewHeight) { // 計算……額……按圖來AN邊~ float an = sizeLong - mViewHeight; // 三角形AMN的MN邊 float largerTrianShortSize = an / (sizeLong - (mViewHeight - mPointY)) * (mViewWidth - mPointX); // 三角形AQN的QN邊 float smallTrianShortSize = an / sizeLong * sizeShort; /* * 計算引數 */ float topX1 = mViewWidth - largerTrianShortSize; float topX2 = mViewWidth - smallTrianShortSize; float btmX2 = mViewWidth - sizeShort; // 計算曲線起點 float startXBtm = btmX2 - CURVATURE * sizeShort; float startYBtm = mViewHeight; // 計算曲線終點 float endXBtm = mPointX + (1 - CURVATURE) * (tempAM); float endYBtm = mPointY + (1 - CURVATURE) * mL; // 計算曲線控制點 float controlXBtm = btmX2; float controlYBtm = mViewHeight; // 計算曲線頂點 float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm; float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm; /* * 生成帶曲線的四邊形路徑 */ mPath.moveTo(startXBtm, startYBtm); mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm); mPath.lineTo(mPointX, mPointY); mPath.lineTo(topX1, 0); mPath.lineTo(topX2, 0); /* * 替補區域Path */ mPathTrap.moveTo(startXBtm, startYBtm); mPathTrap.lineTo(topX2, 0); mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm); mPathTrap.close(); /* * 底部月半圓Path */ mPathSemicircleBtm.moveTo(startXBtm, startYBtm); mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm); mPathSemicircleBtm.close(); /* * 生成包含摺疊和下一頁的路徑 */ //暫時沒用省略掉 // 計算月半圓區域 mRegionSemicircle = computeRegion(mPathSemicircleBtm);} else { /* * 計算引數 */ float leftY = mViewHeight - sizeLong; float btmX = mViewWidth - sizeShort; // 計算曲線起點 float startXBtm = btmX - CURVATURE * sizeShort; float startYBtm = mViewHeight; float startXLeft = mViewWidth; float startYLeft = leftY - CURVATURE * sizeLong; // 計算曲線終點 float endXBtm = mPointX + (1 - CURVATURE) * (tempAM); float endYBtm = mPointY + (1 - CURVATURE) * mL; float endXLeft = mPointX + (1 - CURVATURE) * mK; float endYLeft = mPointY - (1 - CURVATURE) * (sizeLong - mL); // 計算曲線控制點 float controlXBtm = btmX; float controlYBtm = mViewHeight; float controlXLeft = mViewWidth; float controlYLeft = leftY; // 計算曲線頂點 float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm; float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm; float bezierPeakXLeft = 0.25F * startXLeft + 0.5F * controlXLeft + 0.25F * endXLeft; float bezierPeakYLeft = 0.25F * startYLeft + 0.5F * controlYLeft + 0.25F * endYLeft; /* * 限制右側曲線起點 */ if (startYLeft <= 0) { startYLeft = 0; } /* * 限制底部左側曲線起點 */ if (startXBtm <= 0) { startXBtm = 0; } /* * 根據底部左側限制點重新計算貝塞爾曲線頂點座標 */ float partOfShortLength = CURVATURE * sizeShort; if (btmX >= -mValueAdded && btmX <= partOfShortLength - mValueAdded) { float f = btmX / partOfShortLength; float t = 0.5F * f; float bezierPeakTemp = 1 - t; float bezierPeakTemp1 = bezierPeakTemp * bezierPeakTemp; float bezierPeakTemp2 = 2 * t * bezierPeakTemp; float bezierPeakTemp3 = t * t; bezierPeakXBtm = bezierPeakTemp1 * startXBtm + bezierPeakTemp2 * controlXBtm + bezierPeakTemp3 * endXBtm; bezierPeakYBtm = bezierPeakTemp1 * startYBtm + bezierPeakTemp2 * controlYBtm + bezierPeakTemp3 * endYBtm; } /* * 根據右側限制點重新計算貝塞爾曲線頂點座標 */ float partOfLongLength = CURVATURE * sizeLong; if (leftY >= -mValueAdded && leftY <= partOfLongLength - mValueAdded) { float f = leftY / partOfLongLength; float t = 0.5F * f; float bezierPeakTemp = 1 - t; float bezierPeakTemp1 = bezierPeakTemp * bezierPeakTemp; float bezierPeakTemp2 = 2 * t * bezierPeakTemp; float bezierPeakTemp3 = t * t; bezierPeakXLeft = bezierPeakTemp1 * startXLeft + bezierPeakTemp2 * controlXLeft + bezierPeakTemp3 * endXLeft; bezierPeakYLeft = bezierPeakTemp1 * startYLeft + bezierPeakTemp2 * controlYLeft + bezierPeakTemp3 * endYLeft; } /* * 替補區域Path */ mPathTrap.moveTo(startXBtm, startYBtm); mPathTrap.lineTo(startXLeft, startYLeft); mPathTrap.lineTo(bezierPeakXLeft, bezierPeakYLeft); mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm); mPathTrap.close(); /* * 生成帶曲線的三角形路徑 */ mPath.moveTo(startXBtm, startYBtm); mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm); mPath.lineTo(mPointX, mPointY); mPath.lineTo(endXLeft, endYLeft); mPath.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft); /* * 生成底部月半圓的Path */ mPathSemicircleBtm.moveTo(startXBtm, startYBtm); mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm); mPathSemicircleBtm.close(); /* * 生成右側月半圓的Path */ mPathSemicircleLeft.moveTo(endXLeft, endYLeft); mPathSemicircleLeft.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft); mPathSemicircleLeft.close(); /* * 生成包含摺疊和下一頁的路徑 */ //暫時沒用省略掉 /* * 計算底部和右側兩月半圓區域 */ Region regionSemicircleBtm = computeRegion(mPathSemicircleBtm); Region regionSemicircleLeft = computeRegion(mPathSemicircleLeft); // 合併兩月半圓區域 mRegionSemicircle.op(regionSemicircleBtm, regionSemicircleLeft, Region.Op.UNION);}// 根據Path生成的摺疊區域Region regioFlod = computeRegion(mPath);// 替補區域Region regionTrap = computeRegion(mPathTrap);// 令摺疊區域與替補區域相加regioFlod.op(regionTrap, Region.Op.UNION);// 從相加後的區域中剔除掉月半圓的區域獲得最終摺疊區域regioFlod.op(mRegionSemicircle, Region.Op.DIFFERENCE);/* * 根據裁剪區域填充畫布 */canvas.clipRegion(regioFlod);canvas.drawColor(Color.RED);如上程式碼46-49行
/* * 替補區域Path */mPathTrap.moveTo(startXBtm, startYBtm);mPathTrap.lineTo(topX2, 0);mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm);mPathTrap.close();對應程式碼54-56行
/* * 底部月半圓Path */mPathSemicircleBtm.moveTo(startXBtm, startYBtm);mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);mPathSemicircleBtm.close();// 計算月半圓區域mRegionSemicircle = computeRegion(mPathSemicircleBtm);// ………………中間省略巨量程式碼………………// 根據Path生成的摺疊區域Region regioFlod = computeRegion(mPath);// 替補區域Region regionTrap = computeRegion(mPathTrap);// 令摺疊區域與替補區域相加regioFlod.op(regionTrap, Region.Op.UNION);// 從相加後的區域中剔除掉月半圓的區域獲得最終摺疊區域regioFlod.op(mRegionSemicircle, Region.Op.DIFFERENCE);兩一種情況則稍微複雜些,除了要計算底部,我們還要計算右側的月半圓Path區域,程式碼165-174:
/* * 生成底部月半圓的Path */mPathSemicircleBtm.moveTo(startXBtm, startYBtm);mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);mPathSemicircleBtm.close();/* * 生成右側月半圓的Path */mPathSemicircleLeft.moveTo(endXLeft, endYLeft);mPathSemicircleLeft.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft);mPathSemicircleLeft.close();替補區域的計算,147-151:/* * 替補區域Path */mPathTrap.moveTo(startXBtm, startYBtm);mPathTrap.lineTo(startXLeft, startYLeft);mPathTrap.lineTo(bezierPeakXLeft, bezierPeakYLeft);mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm);mPathTrap.close();區域的轉換,184-188:/* * 計算底部和右側兩月半圓區域 */Region regionSemicircleBtm = computeRegion(mPathSemicircleBtm);Region regionSemicircleLeft = computeRegion(mPathSemicircleLeft);// 合併兩月半圓區域mRegionSemicircle.op(regionSemicircleBtm, regionSemicircleLeft, Region.Op.UNION);結合兩種情況,我們可以得到下面的效果:
然後,我們需要計算“下一頁”的區域,同樣,根據上一節我們的講解,我們先獲取摺疊區域和下一頁區域之和再減去摺疊區域就可以得到下一頁的區域:
mRegionNext = computeRegion(mPathFoldAndNext);mRegionNext.op(mRegionFold, Region.Op.DIFFERENCE);最後,我們結合上兩節,注入資料:
/** * 繪製點陣圖資料 * * @param canvas * 畫布物件 */private void drawBitmaps(Canvas canvas) { // 繪製點陣圖前重置isLastPage為false isLastPage = false; // 限制pageIndex的值範圍 mPageIndex = mPageIndex < 0 ? 0 : mPageIndex; mPageIndex = mPageIndex > mBitmaps.size() ? mBitmaps.size() : mPageIndex; // 計算資料起始位置 int start = mBitmaps.size() - 2 - mPageIndex; int end = mBitmaps.size() - mPageIndex; /* * 如果資料起點位置小於0則表示當前已經到了最後一張圖片 */ if (start < 0) { // 此時設定isLastPage為true isLastPage = true; // 並顯示提示資訊 showToast("This is fucking lastest page"); // 強制重置起始位置 start = 0; end = 1; } /* * 計算當前頁的區域 */ canvas.save(); canvas.clipRegion(mRegionCurrent); canvas.drawBitmap(mBitmaps.get(end - 1), 0, 0, null); canvas.restore(); /* * 計算摺疊頁的區域 */ canvas.save(); canvas.clipRegion(mRegionFold); canvas.translate(mPointX, mPointY); /* * 根據長短邊標識計算摺疊區域影象 */ if (mRatio == Ratio.SHORT) { canvas.rotate(90 - mDegrees); canvas.translate(0, -mViewHeight); canvas.scale(-1, 1); canvas.translate(-mViewWidth, 0); } else { canvas.rotate(-(90 - mDegrees)); canvas.translate(-mViewWidth, 0); canvas.scale(1, -1); canvas.translate(0, -mViewHeight); } canvas.drawBitmap(mBitmaps.get(end - 1), 0, 0, null); canvas.restore(); /* * 計算下一頁的區域 */ canvas.save(); canvas.clipRegion(mRegionNext); canvas.drawBitmap(mBitmaps.get(start), 0, 0, null); canvas.restore();}該部分的程式碼就不貼出了,大部分跟上一節相同,因為過兩天要去旅遊時間略緊這節略講得粗糙,不過也沒什麼太大的改動,如果大家有不懂的地方可以留言或群裡@哥,下一節我們將嘗試實現翻頁時影象扭曲的效果。
原始碼地址:傳送門