Leetcode 84 柱狀圖中最大的面積
給定 n 個非負整數,用來表示柱狀圖中各個柱子的高度。每個柱子彼此相鄰,且寬度為 1 。
求在該柱狀圖中,能夠勾勒出來的矩形的最大面積。
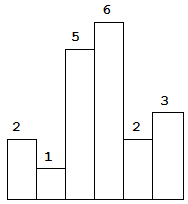
以上是柱狀圖的示例,其中每個柱子的寬度為 1,給定的高度為 [2,1,5,6,2,3]。
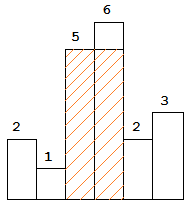
圖中陰影部分為所能勾勒出的最大矩形面積,其面積為 10 個單位。
示例:
輸入: [2,1,5,6,2,3] 輸出: 10
一開始看到後想也沒想就用暴力解法去做 方法就是當寬為1時,即比較每個陣列中最大的那個元素值,寬為2時,比較相鄰兩個元素之間取最小的值,遍歷完一邊後找到相鄰元素之間最小的值的集合中最大的值,寬為3的話也是以此類推,比較相鄰三個元素之間取最小值然後取集合中最大的值
程式碼如下:
class Solution { public: int largestRectangleArea(vector<int>& heights) { int size=heights.size(); if(size==0)return 0; if(size==1)return heights[0]; int maxres=INT_MIN; int minres=INT_MIN; vector<int>res; vector<int>first; int count=1; for(int i=0;i<size;i++){ first.push_back(heights[i]); } sort(first.begin(),first.end()); maxres=first[first.size()-1]; for(int i=1;i<size;i++){ count++; res=fun(heights); heights.clear(); for(int k=0;k<res.size();k++){ heights.push_back(res[k]); } sort(res.begin(),res.end()); minres=res[res.size()-1]; maxres=max(maxres,count*minres); } return maxres; } vector<int> fun(vector<int>& temp){ vector<int>res; if(temp.size()==1)res.push_back(temp[0]); for(int i=1;i<temp.size();i++){ if(temp[i]>temp[i-1]){ res.push_back(temp[i-1]); }else{ res.push_back(temp[i]); } } return res; } };
然後一跑,果然 測試到最後2個例子就超出時間限制了 時間複雜度為O(n的2次方)
然後就去網上查閱了一下方法 用到了單調棧於是記錄一下方法
思路大概就是這樣:如果我們的陣列是升序的話 例如:5 6 7 8 9 那麼我們解的集合就是從5*5,6*4,7*3,8*2,9*1中去取
所以我們為了往升序的陣列靠近 就用到單調棧,通過比較當前棧頂元素值和當前陣列heights[i]的大小,如果棧頂元素小於當前陣列heights[i]就加入棧中,否則將棧頂元素移除pop,並且記錄此時的矩形面積=移除的元素*移除的個數。移除後繼續與棧頂元素比較依次迴圈直至棧頂元素小於當前陣列heights[i]然後加入棧中。
例如題目中 :2 1 5 6 2 3
首先我們將0加入棧中 不會引發錯誤
然後① 2>0 直接加入棧頂 繼續
② 1<棧頂元素2 所以將2移除棧 將1加入棧中 此時記錄面積2 *1 =2
③5>1 直接加入棧中 1 5
④6>5 直接加入棧中 1 5 6
⑤2<棧頂元素6 將6移除 此時記錄面積為6*1 繼續 2<棧頂元素5 將5移除 此時記錄面積為5*2 繼續 2>1 所以將2加入棧中 1 2
⑥3>2 直接加入棧中 此時棧中元素 1 2 3 通過一開始那個升序方法求得 這個的面積集合有1*3,2*2 ,3*1
⑦我們只要將上面最大的面積取出來即是答案
程式碼如下:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
// Exceptional Case:
if(n == 0){
return 0;
}
if(n == 1){
return heights[0];
}
// insert 0 height
heights.push_back(0);
stack<int> st;
int ans = 0;
for(int i = 0; i <= n; i++){
if(st.empty() || heights[i] >= heights[st.top()]){
st.push(i);
}
else{
int top = st.top();
st.pop();
int w = st.empty()? i: i - 1 - st.top();
ans = max(ans, heights[top] * w);
i--;
}
}
return ans;
}
};
