幾種排序方法
一、選擇排序
原理:
1、依次比較陣列中元素,從而記錄下陣列中最小的元素
2、將最小元素與陣列第一個元素交換
3、依次比較陣列中剩餘元素,從而記錄下剩餘陣列中最小的元素 與陣列第二個元素交換,以此類推
特點:
需要大約(N-1)+(N-2)+....+1 ~ N^2/2次比較和N次交換,演算法的時間效率取決於比較的次數。

程式碼:
#include<iostream> using namespace std; template <class T> void select_sort(T *a, int len) { for (int i = 0; i < len; i++){ int min = i; for (int j = i + 1; j < len; j++) if (a[i] > a[j]) min = j; T t = a[min]; a[min] = a[i]; a[i] = t; } for (int i = 0; i != len; i++) { cout << a[i] <<" "; } } int main() { int a[3]={1, 3, 2}; select_sort(a, 3); system("pause"); return 0; }
結果:
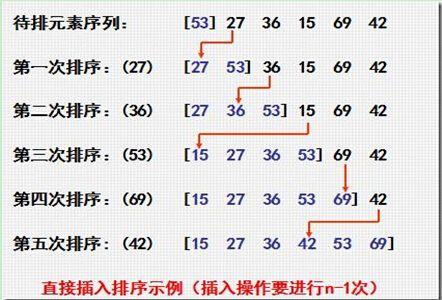
二、插入排序
原理:
1、從陣列的第一個元素出發 不斷的向右移動
2、每走一步把之前的元素排序
特點:
插入排序所需要的時間取決於輸入中元素的初始順序。對於一個很大的且其中的元素已經有序的陣列進行排序要比隨機的陣列快的多。至少要進行N-1次比較和0次交換,最多需要大約N^2/2次比較和交換。平均N^2/4次比較和交換。
程式碼:
#include<iostream> using namespace std; template <class T> void insert_sort(T *a, int len) { int i, j; for (i = 1; i < len; i++){ T tem = *(a + i); for (j = i; j != 0 && *(a + j - 1) > tem; j--) *(a + j) = *(a + j - 1); *(a + j) = tem; } for (int n = 0; n != len; n++) { cout << a[n] <<" "; } } int main() { int a[3]={1, 3, 2}; insert_sort(a, 3); system("pause"); return 0; }
三、氣泡排序
原理:
1、從陣列的第一個元素開始,比較前兩個元素大小,大的替換較後的位置
2、在依次比較二三號位置的數值,直到陣列末尾n為一個迴圈,這時最大的數移動到陣列末尾,其他順序不變
3、按照上述方法比較前n-1個元素
特點:
最簡單基本的的排序方式
程式碼
#include<iostream> using namespace std; template <class T> void bubble_sort(T *a, int len) { T tem; for (int i = 1; i != len; i++) { for (int j = i; j != len; j++) { if (a[j] < a[j - 1]) { tem = a[j]; a[j] = a[j - 1]; a[j - 1] = tem; } } } for (int i = 0; i < len; i++) { cout << a[i]; } } int main() { int a[3]={1, 3, 2}; insert_sort(a, 3); system("pause"); return 0; }
四、桶排序
簡單的桶排序:
原理:
1、給定一組數a[],其中最大的數為max,定義一個數組b[],長度為max+1
2、將陣列中的數都置零,遍歷給定的a[]中的元素i, 在對應陣列b[]索引為i的位置加1
3、最終輸出b中元素值的索引
特點:

程式碼:
#include<iostream>
using namespace std;
template <class T>
void insert_sort(T *a, int len)
{
int m, n;
T *b = new T[len+1];
for (n = 0; n != len + 1; n++)
{
b[n] = 0;
}
for (m = 0; m != len; m++)
{
b[a[m]]++;
}
for (int i = 0; i < len + 1; i++)
{
for (int j = 0; j != b[i]; j++)
cout << i;
}
}
int main()
{
int a[3]={1, 3, 2};
insert_sort(a, 3);
system("pause");
return 0;
}複雜一點的桶排序
原理:
和簡單的桶排序差不多隻不多陣列不在是max+1,而是分成幾個區間
每個桶用一個連結串列表示,桶中放著相應的元素
//每一個節點的結構
struct node
{
int key; //關鍵字,在桶中統計桶中資料量,在資料節點中就是節點的資料
struct node *next;
};
//宣告:
void PrintBucketSort(node** bucket, int bucket_size);
int f(int x);
void BucketSort(int* a, int size,int bucket_size)
{
assert(a);
//給桶申請空間
node** bucket = new node*[bucket_size*sizeof(node)];
//初始化
for (int i = 0; i < bucket_size; ++i)
{
bucket[i] = new node[sizeof(node)]; //每一個桶
bucket[i]->key = 0;
bucket[i]->next = nullptr;
}
for (int j = 0; j < size; ++j)
{
node* sub_node = new node[sizeof(node)]; //桶下的每一個節點
sub_node->key = a[j];
sub_node->next = nullptr;
//計算這資料在哪個桶中
int num = f(a[j]);
//讓一個指標指向這個桶號的頭
node* sub_head = bucket[num];
//開始插入
if (sub_head->next == nullptr)
{
bucket[num]->next = sub_node;
bucket[num]->key++;
}
//該桶號不為空,那麼插入排序
else
{
while (sub_head->next != nullptr && sub_node->key >= sub_head->next->key)
{
sub_head = sub_head->next;
}
sub_node->next = sub_head->next;
sub_head->next = sub_node;
bucket[num]->key++;
}
}
//列印
PrintBucketSort(bucket, bucket_size);
}
//對映函式
int f(int x)
{
return (x / 10);
}
//列印
void PrintBucketSort(node** bucket, int bucket_size)
{
//多少桶鏈(桶號)
for (int i = 0; i < bucket_size; ++i)
{
node* cur = bucket[i]->next;
while (cur)
{
cout << cur->key << " ";
cur = cur->next;
}
}
cout << endl;
}
void Test7()
{
int a[10] = { 49, 38, 35, 97, 76, 73, 27, 49, 34, 78 };
cout << "桶排序" << endl;
BucketSort(a, 10, 10); //桶資料最大才97,所以需要10個桶
} 五、歸併排序
原理:要將一個數組排序,先將他分成兩半分別進行排序,然後再把結果歸併起來
特點:能夠保證將任意長度為N的陣列排序所需時間和NLogN成正比,缺點是所需的空間和NLogN成正比。
程式碼:
#include<iostream>
using namespace std;
template<class T>
void Merge(T* A, T* left, int leftCount, int *right, int rightCount)
{
int i = 0;
int j = 0;
int n = 0;
while (i < leftCount && j < rightCount)
{
if (*(left + i) < *(right + j))
{
*(A + n) = *(left + i);
i++; n++;
}
else
{
*(A + n) = *(right + j);
j++; n++;
}
}
while (i < leftCount) {
*(A + n) = *(left + i); n++; i++;
}
while (j < rightCount) {
*(A + n) = *(right + j); n++; j++;
}
}
template<class T>
void Merge_sort(T *A, int n)
{
int mid, i;
T *left, *right;
if (n < 2) return;
mid = n / 2;
left = new T[mid];
right = new T[n - mid];
for (i = 0; i < mid; i++) *(left + i) = *(A + i);
for (i = mid; i < n; i++) *(right+i - mid) = *(A + i);
Merge_sort(left, mid);
Merge_sort(right, mid);
Merge(A, left, mid, right, n - mid);
delete[] right;
delete[] left;
}
int main()
{
int A[] = { 6, 2, 3, 1, 9, 10, 15, 13, 12, 17 }; // creating an array of integers.
int i, numberOfElements;
numberOfElements = sizeof(A) / sizeof(A[0]);
// Calling merge sort to sort the array.
Merge_sort(A, numberOfElements);
for (i = 0; i < numberOfElements; i++)
cout << " " << A[i];
system("pause");
return 0;
}各演算法複雜度:



