1.曼哈頓距離

曼哈頓距離又稱馬氏距離（Manhattan distance），用以標明兩個點上在標準座標系上的絕對軸距之總和。

例如在平面上，座標（x1, y1）的點P1與座標（x2, y2）的點P2的曼哈頓距離為：

2.歐式距離

歐式距離又稱歐幾里得距離或歐幾里得度量（Euclidean Metric），以空間為基準的兩點之間最短距離，與之後的切比雪夫距離的差別是，只算在空間下。

說的通俗點，就是初中知識，兩點之間直線最短的概念。

3.切比雪夫距離

切比雪夫距離又稱（Chebyshev distance）或者（Supremum distance）。數學上，切比雪夫距離（Chebyshev distance）或是L∞度量是向量空間中的一種度量，二個點之間的距離定義為其各座標數值差的最大值。

例如，兩個人同時從A到B，二者經歷的歐式距離來相等，但由於存在其他維度上的差異（比如交通方式），切比雪夫距離可能不同。

4.明式距離

明氏距離又叫做明可夫斯基距離（Minkowski distance）。

當緯度等於1時候，其公式等價於曼哈頓距離。

等於2時候，其公式等價於歐式距離。

當大於2到無窮大時候，其公式等價於切比雪夫距離。

5.漢明距離

漢明距離是以理查德·衛斯里·漢明的名字命名的。在資訊理論中，兩個等長字串之間的漢明距離是兩個字串對應位置的不同字元的個數。換句話說，它就是將一個字串變換成另外一個字串所需要替換的字元個數。例如：

ab 與ac 有一個字元不同，漢明距離是1
ab與ca有兩個字元不同，漢明距離是2
1011101 與 1001001 之間的漢明距離是 2。
2143896 與 2233796 之間的漢明距離是 3。
"toned" 與 "roses" 之間的漢明距離是 3。

6.餘弦距離

也稱為餘弦相似度，是用向量空間中兩個向量夾角的餘弦值作為衡量兩個個體間差異的大小的度量。

向量，是多維空間中有方向的線段，如果兩個向量的方向一致，即夾角接近零，那麼這兩個向量就相近。而要確定兩個向量方向是否一致，這就要用到餘弦定理計算向量的夾角。

餘弦定理描述了三角形中任何一個夾角和三個邊的關係。給定三角形的三條邊，可以使用餘弦定理求出三角形各個角的角度。假定三角形的三條邊為a，b和c，對應的三個角為A，B和C，那麼角A的餘弦為：

如果將三角形的兩邊b和c看成是兩個向量，則上述公式等價於：

其中分母表示兩個向量b和c的長度，分子表示兩個向量的內積。

7.大圓距離

大圓距離（英語：Great-circle distance）指的是從球面的一點A出發到達球面上另一點B，所經過的最短路徑的長度。一般說來，球面上任意兩點A和B都可以與球心確定唯一的大圓，這個大圓被稱為黎曼圓，而在大圓上連線這兩點的較短的一條弧的長度就是大圓距離。若這兩點和球心正好都在球的直徑上，則過這三點可以有無數大圓，但兩點之間的弧長都相等，且等於該大圓周長的一半{\displaystyle \pi r}, r 是球的半徑。

計算公式如下圖

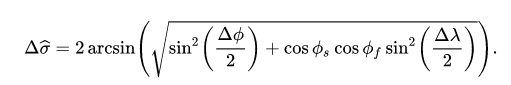
8.李距離

在編碼理論裡，"李"距離是評價兩個長度為n,q進位制的字串和之間的距離，. 它在國際單位制中定義為

當或者，李距離等價於漢明距離。

由李距離所長產生的度量空間是一個類似於離散的橢圓幾何

例如：

假設，字串3340和2543之間的李距離是1+2+0+3=6

參考：

3. wiki百科