定理： 已知前序和中序遍歷，可以確定一棵二叉樹。已知中序和後序遍歷，可以確定一棵二叉樹。但是，已知前序和後序遍歷，不能確定一棵二叉樹。換句話說，已知中序遍歷和前序遍歷或後序遍歷能夠確定一顆二叉樹。

題目描述

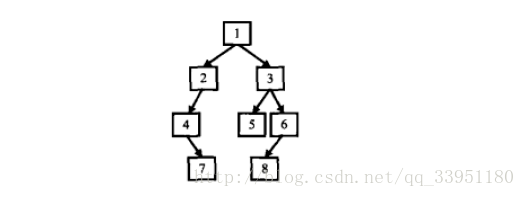
輸入某二叉樹的前序遍歷和中序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷結果中都不含重複的數字。例如輸入前序遍歷序列｛1,2,4,7,3,5,6,8｝和中序遍歷序列｛4,7,2,1,5,3,8,6｝，則重建出如圖所示的二叉樹並輸出它的頭結點。

分析及實現：

根據二叉樹前序遍歷的特點（根-左-右），每次讀取的第一個值一定是根節點，這樣我們可以在中序遍歷的序列中找到當前的根節點的位置。 根據中序遍歷的特點（左-根-右），當確定了一個根節點後，其左邊序列就是這個根節點的左子樹，右邊序列就是其右子樹。

//根據前序遍歷和中序遍歷重建二叉樹
Node* RebuildTree(vector<int> prev, vector<int> vin)
{
    if (prev.empty() || vin.empty())
        return NULL;

    //在前序遍歷中prev中找根節點，並確定其在vin的位置
    size_t index = 0;
    for (; index<vin.size(); index++)
    {
        if (vin[index] == prev[0])
            break;
    }
    //已經找到根節點，並構造根節點
    Node* root = new Node(prev[0]);
    //Print(root);
    //根據中序遍歷將根節點左右兩側一分為二，根節點的左側為左子樹，右側為右子樹
    vector<int> prev_left,prev_right;
    vector<int> vin_left,vin_right;
    //先將前序、中序中根節點的左右子樹記錄下來
    for (size_t j=0; j<index; j++)
    {
        prev_left.push_back(prev[j+1]);
        vin_left.push_back(vin[j]);
    }
    for (size_t j=index+1; j<vin.size(); j++)
    {
        prev_right.push_back(prev[j]);
        vin_right.push_back(vin[j]);
    }
    //遞迴構造左右子樹
    root->_left = RebuildTree(prev_left,vin_left);
    root->_right = RebuildTree(prev_right,vin_right);

    return root;
}