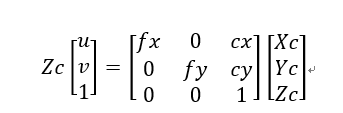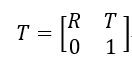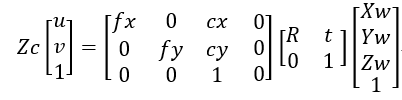前言：

發呆了一個寒假，在開學之前乾點什麼吧~

歡迎指出文章的不足之處~

//---------------------------------------------------------------------------------------------------------------------------

世界座標系：物體的真實世界座標（三維）

相機座標系：相對於相機建立的座標系（三維）

影象座標系：成像面上以光軸為原點的座標系（二維）

畫素座標系：成像面上以左上角為原點的座標系（二維），注意單位是整形的，因為畫素是一個一個的。

齊次座標：可以簡單的理解成用多一維表示低緯的座標。

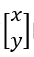
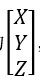
例如的齊次形式可以表示為,對應的關係為

x=X/Z

y=Y/Z

一般可以令Z=1,則x=X,y=Y

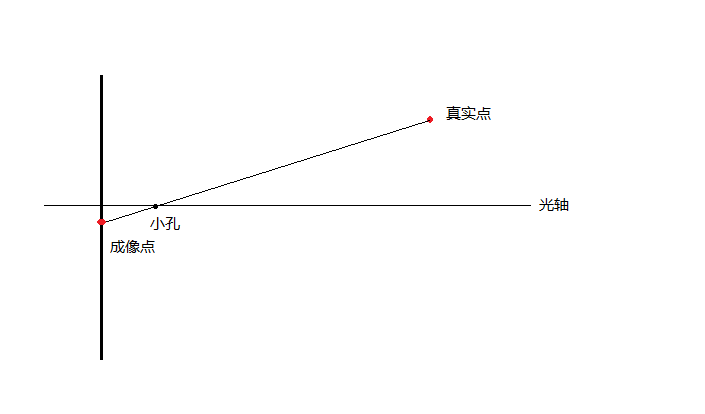
相機成像的原理就是小孔成像的原理如圖所示。

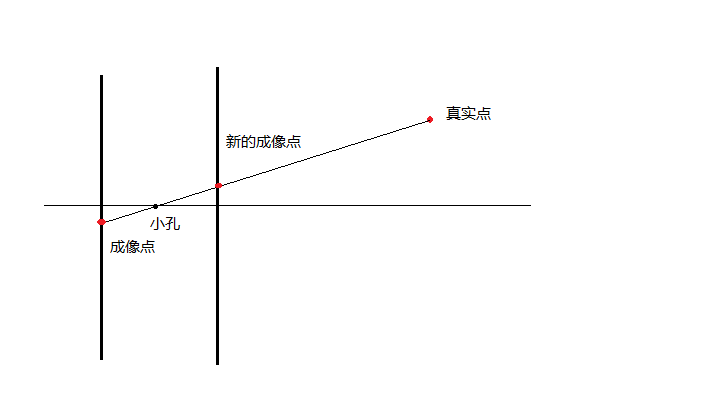
由於小孔成像會導致成像翻轉問題，一般相機都會處理成正立的影象。數學上直接把成像面放置到小孔前面，這樣思考問題會比較簡單，並且結果一致

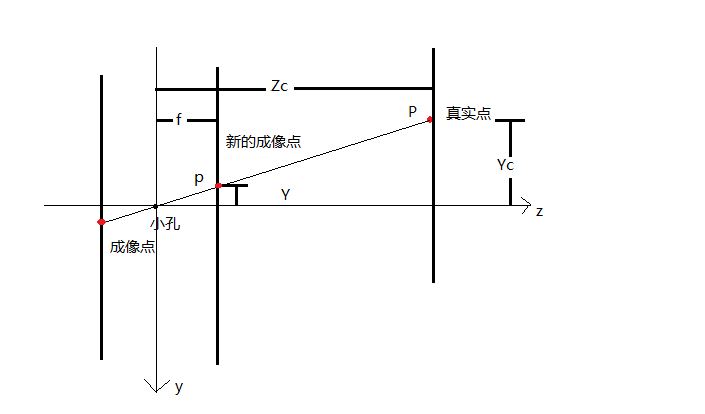
接下來開始推導相機成像的數學模型，所用到的數學知識也只有相似三角形的知識。

設P(Xc,Yc,Zc),p(X,Y,Z),根據相似三角形的知識，可以得到

X=Xc/Zc*f

Y=Yc/Zc*f

Z=f

到這裡已經把相機座標系轉化到了圖片座標系，但是我們常用的是畫素座標系，所以還要繼續進行轉化。

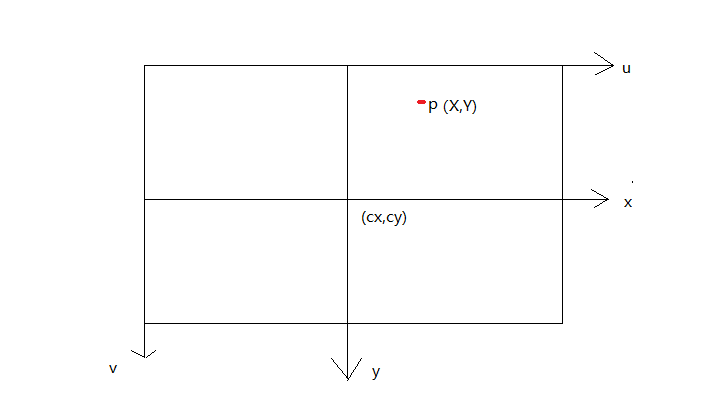
設p點的畫素座標為(u,v)，每個畫素塊的寬度是dx，高度是dy（可以將圖片想象成一個矩陣，裡面密集的排列著很多個光感器件，每個光感器件便是一個畫素，光感器件的寬度便是dx，高度便是dy），理想情況下(cx,cy)為影象的中心點，但是由於相機安裝製作過程中會有這樣或那樣的問題，所以一般來說cx，cy不會剛剛好是圖片的中心點。則u-cx=X/dx,v-cy=Y/dy

變形並且帶入之前所推導的結果，可得

u=Xc/Zc*fx+cx

v=Yc/Zc*fy+cy

其中

fx=f/dx

fy=f/dy

將上式子寫成矩陣的形式為

稱矩陣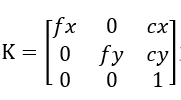為內參數矩陣。

到目前位置，我們所有的一切都是建立在相機座標系上的推導，但是一般來講，世界座標系和相機座標系不會是同一個，我們需要將世界座標系轉換到相機座標系。任何兩個三維座標系之間都只差一個旋轉矩陣R和平移矩陣t，Pc=RPw+t

R是一個3*3的正交矩陣，t是一個3*1的向量。

將R和T寫在一起，並且表示為齊次座標的形式為

T稱為外引數矩陣，將內外引數矩陣寫在一起

到此便是整個相機模型了，注意有Zc

之後若有興趣可以接著看標定的文章

相機標定的數學原理及其推導過程

參考連線：

https://www.cnblogs.com/wangguchangqing/p/8126333.html