假設檢驗(一)總體分佈已知
總體分佈已知時,對總體X的分佈中的引數提出的檢驗問題又稱引數假設檢驗問題
基本概念
-
原假設:H0:θ∈Θ0
-
備擇假設:H1:θ∈Θ1
-
拒絕域:W={(x1,x2,…,xn):T(x)≥c}
-
接受域:Wc={(x1,x2,…,xn):T(x)<c}
-
拒絕原假設H0:(x1,x2,…,xn)∈ W
其中T(x)是能從樣本空間劃分出拒絕域的統計量,稱為檢驗統計量;c是一個待定的常數,稱其為檢驗的臨界值 -
檢驗函式:拒絕域上的示性函式
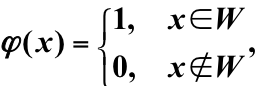
-
第一類錯誤:H0為真時,拒絕原假設,其概率為:
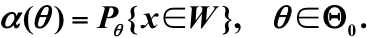
-
第二類錯誤:H0為假時,接受原假設,其概率為:
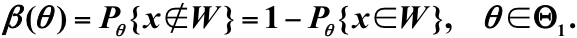
-
檢驗的勢(功效):當H0不成立時拒絕它的概率(這回是對的):
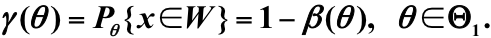
-
勢函式(功效函式):檢驗犯第一類錯誤的概率:
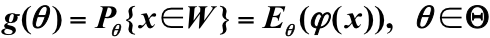
當θ∈Θ0時,g(θ)=α(θ)
當θ∈Θ1時,g(θ)=γ(θ) -
Neyman-Pearson檢驗原理:控制犯第一類錯誤的概率在給定的範圍內,尋找檢驗量使犯第二類錯誤的概率儘可能小(即使檢驗的功效儘可能大),即給定一個較小的數α∈(0<α<1),在滿足
Pθ{x∈W}=Eθ(φ(x))≤α, θ∈Θ0
的檢驗函式中,尋找勢儘可能大的檢驗函式 -
水平為α的檢驗:φ(x)滿足Eθ(φ(x))≤α,其中θ∈Θ0,α(0<α<1)
-
檢驗的大小(真實水平):對任何滿足α<α′≤1的α′,φ(x)也是水平為α′的檢驗,稱
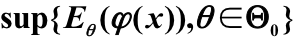
為檢驗φ(x)的大小或真實水平
相關推薦
假設檢驗(一)總體分佈已知
總體分佈已知時,對總體X的分佈中的引數提出的檢驗問題又稱引數假設檢驗問題 基本概念 原假設:H0:θ∈Θ0H_0:\theta\in\Theta_0H0:θ∈Θ0 備擇假設:H1:θ∈Θ1H_1:\theta\in\Theta_1H1:θ∈Θ1
Sail.js官方文件閱讀筆記(一)——總體結構
sails.js是一個後端開發框架,它是基於Node的著名框架express之上的。當前工作接手了一個系統,該系統的console部分是以sails.js完成其前後端功能的,故學習了sails.js的部分官方文件,特以此係列筆記以記之。因初學乍練,如有錯誤,歡迎指正。 在官網中,使用Sail
[轉帖]VMware Vsphere 6.0安裝部署 (一) 總體部署架構
(一)總體部署架構本教程用於學習目的,力求詳盡的介紹安裝部署過程和各元件之間的關係,部署過程從最簡單的模型開始,系列文章按時間順序依次展開,每篇介紹一個元件。 開始階段,按照一臺物理伺服器,部署所有VMware元件的模型進行,這也是為了貼近大部分初學者在沒有就職於商業機構,缺乏實際測試,生產環境的情形下,利
假設檢驗(總結)
假設檢驗是數理統計學中根據一定假設條件由樣本推斷總體的一種方法。具體的做法是:根據問題需要對研究的總體做某種假設記作H0;選取合適的統計量,這個統計量要是的假設H0成立時,其分佈已知。這樣我們就可以根據統計量的分佈是否滿足某種分佈,並根據預先設定的顯著性水平進行
libevent原始碼解讀(一)--總體閱讀
我學習新東西的方法是對新東西有個大概的瞭解,然後在逐步深入。我不知道這種方法好不好,如果有什麼好的學習方法,望推薦! 廢話少說,先下載原始碼然後安裝。本人使用的原始碼是穩定版的libevent-2.0.6。至於他的詳細更新,可以到他的程式碼庫去看。https
Framebuffer 驅動學習總結(一) ---- 總體架構及關鍵結構體
一、Framebuffer 裝置驅動總體架構 幀緩衝裝置為標準的字元型裝置,在Linux中主裝置號29,定義在/include/
高併發&效能優化(一)------總體介紹
【開篇詞】 本文主要通過一些經典的高併發場景,以及一些基本的運維工具來講述一些關於高併發以及效能優化相關的內容,主要包括效能瓶頸的定位,效能調優的思路和技巧等。 【效能的衡量指標】 ?什麼是效能 效能就是,在有限的時間內,使用有限的資源,完成任務。 在儲存資源成本越來越低
企業級自定義表單引擎解決方案(一)--總體介紹
大家回想一下,有多少軟體公司,多少專案,多少初中級程式設計師在做著CRUD方面的一些重複而繁雜的工作呢?對於公司專案來說,可能60-70%的成本都花費在CRUD方面的開發管理上,對於程式設計師職業生涯來說,可能也有60-70%的工作也是在做著一些CRUD方面的工作,無可否認,作者也是。 如果這些CRU
ABP總體介紹 - 入門介紹(一)
通知 模式 5.0 control 技術 BE lock erp 支持 ABP是“ASP.NET Boilerplate Project (ASP.NET樣板項目)”的簡稱。 ASP.NET Boilerplate是一個用最佳實踐和流行技術開發現代WEB應用程序的新起點,它
假設檢驗(Hypothesis Testing)
基本思想 ddc 控制 .com bcd 樣本 course bbf 正態分布 什麽是假設檢驗 假設檢驗是用來判斷樣本與樣本,樣本與總體的差異是由抽樣誤差引起還是本質差別造成的統計推斷方法。其基本原理是先對總體的特征作出某種假設,然後通過抽樣研究的統計推理,對此假
基於Maven的SSM總體架構設計(一)
基於Maven的SSM總體架構設計(一) 1 概述 1.1 編寫目的 1.2 讀者物件 1.3 引用檔案 1.4 術語表 2 相關技術介紹 2.1 Spring框架介紹 2.1.1
關於Unity3D開發三星Gear VR的初步嘗試(一):已實現打包到手機顯示
這兩天老師催我把前段時間買的三星GearVR在Unity3D嘗試打包,不然就白買了,到現在已經成功實現了打包。我把記錄貼下來,以免未來可能用。 1.需要的硬體:三星GearVR、三星s8+(其他的幾代應該也可以) 2.需要的軟體:Unity3D(本人使用的是2017.4.2f2版本)、J
Vue專案實戰優化:已有元件優化系列(一)
一_原有元件效果 其中,核取方塊為一個元件,根據資料庫中的值,進行是否勾選,並且核取方塊只能是禁用的 二_原有元件程式碼 <template> <input v-if="gearboxtype === 'A'" checked type="
centos7下Hadoop2.8.4全分佈搭建之HDFS叢集搭建(一)
1)搭建前的準備 注意:(以下操作可以先配置一臺,然後通過scp命令傳送到其他兩臺虛擬機器上 傳送到其他機器 scp -r 主機名: 注意:載入環境變數 source /etc/profile
Java設計模式之總體簡介(一)——簡單易懂
設計模式(Design pattern)是一套被反覆使用、多數人知曉的、經過分類編目的、程式碼設計經驗的總結。使用設計模式是為了可重用程式碼、讓程式碼更容易被他人理解、保證程式碼可靠性。 毫無疑問,設計模式於己於他人於系統都是多贏的,設計模式使程式碼編制真正工程化,設計模式是
野牛NBIOT 環境監測專案---總體介紹(STM32L4+BC35)(一)
本部落格文件以Demo專案形式和同學們一起學習STM32L4+BC35 1、專案目的及願景: 這個環境監測Demo專案主要需要完成以下功能: 1、通過低功耗MCU採集溫度、溼度、光照 2、通過NBIOT模組將資料傳送至後臺 3、PC端或者
(一)HDFS總體架構
1、背景 海量的非結構化資料,幾乎沒法梳理成一個個的欄位,來儲存在關係型資料庫中。所以實際應用中,對於這類資料需要考慮資料如何儲存。資料如何計算的問題。 2、hadoop兩個核心 HDFS(以分散式方式來儲存海量資料) MapReduce(以HDFS上的資料為基礎進行計算
目標檢測(一)--Objectness演算法總體理解,整理及總結
1.原始碼下載及轉換為VS2012 WIN32版本。 http://www.cnblogs.com/larch18/p/4560690.html 2.原文: http://wenku.baidu.com/link?url=ls5vmcYnsUdC-ynKdBzWgx
(一)我的畢業設計之總體概述篇
經過兩個月的開發,我的畢業設計-《校園網溝通平臺》終於基本開發完成了,感到非常高興,但由於時間緊迫,還要趕著寫論文,所以肯定存在很多bug,希望大家多給點建議,同時歡迎使用校園網的同學幫手執行測試,先謝謝了。 技術簡介:我的設計是基於SOA架構的,主要採用微
理論分佈和抽樣分佈------(一)事件、概率和隨機變數(離散、連續)
抽樣分佈:從間斷性變數總體的理論分佈(二項分佈和泊松分佈)和連續性變數總體的理論分佈中抽出的樣本統計數的分佈,即抽樣分佈。 一、事件和事件發生的概率 事件:在自然界中一種事物,常存在幾種可能出現的情況,每一種可能出現的情況稱為事件 事件的概率:每一件事出現的可能性,稱為
