資料結構開發(21):樹中屬性操作與層次遍歷
阿新 • • 發佈:2018-12-21
0.目錄
1.樹中屬性操作的實現
2.樹形結構的層次遍歷
3.小結
1.樹中屬性操作的實現
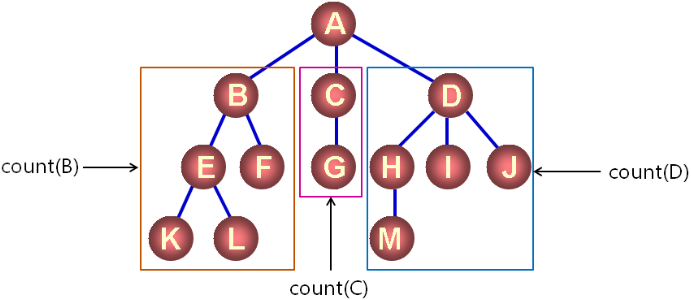
樹中結點的數目:
- 定義功能:count(node)
- 在 node 為根結點的樹中統計結點數目

樹結點數目的計算示例:
- count(A) = count(B) + count(C) + count(D) + 1
在GTree.h中實現統計結點數目:
protected: int count(GTreeNode<T>* node) const { int ret = 0; if( node != NULL ) { ret = 1; for(node->child.move(0); !node->child.end(); node->child.next()) { ret += count(node->child.current()); } } return ret; } public: int count() const { return count(root()); }
樹的高度:
- 定義功能:height(node)
- 獲取 node 為根結點的樹的高度

樹的高度計算示例:
- height(A) = MAX{ height(B), height(C), height(D) } + 1

在GTree.h中實現獲取樹的高度:
protected: int height(GTreeNode<T>* node) const { int ret = 0; if( node != NULL ) { for(node->child.move(0); !node->child.end(); node->child.next()) { int h = height(node->child.current()); if( ret < h ) { ret = h; } } ret = ret + 1; } return ret; } public: int height() const { return height(root()); }
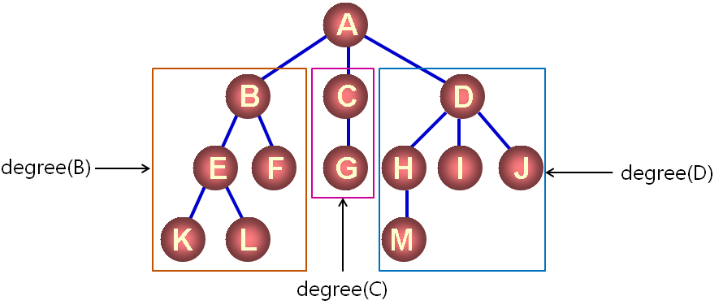
樹的度數:
- 定義功能:degree(node)
- 獲取 node 為根結點的樹的度數

樹的度計算示例:
- degree(A) = MAX{ degree(B), degree(C), degree(D), 3 }
在GTree.h中實現獲取樹的度數:
protected: int degree(GTreeNode<T>* node) const { int ret = 0; if( node != NULL ) { ret = node->child.length(); for(node->child.move(0); !node->child.end(); node->child.next()) { int d = degree(node->child.current()); if( ret < d ) { ret = d; } } } return ret; } public: int degree() const { return degree(root()); }
統一mian.cpp測試:
#include <iostream>
#include "GTree.h"
using namespace std;
using namespace StLib;
int main()
{
GTree<char> t;
GTreeNode<char>* node = NULL;
GTreeNode<char> root;
root.value = 'A';
root.parent = NULL;
t.insert(&root);
node = t.find('A');
t.insert('B', node);
t.insert('C', node);
t.insert('D', node);
node = t.find('B');
t.insert('E', node);
t.insert('F', node);
node = t.find('E');
t.insert('K', node);
t.insert('L', node);
node = t.find('C');
t.insert('G', node);
node = t.find('D');
t.insert('H', node);
t.insert('I', node);
t.insert('J', node);
node = t.find('H');
t.insert('M', node);
cout << t.count() << endl;
cout << t.height() << endl;
cout << t.degree() << endl;
return 0;
}執行結果為:
13
4
32.樹形結構的層次遍歷
問題:
- 如何按層次遍歷通用樹結構中的每一個數據元素?
當前的事實:
- 樹是非線性的資料結構,樹的結點沒有固定的編號方式
新的需求:
- 為通用樹結構提供新的方法,快速遍歷每一個結點
設計思路(遊標):
- 在樹中定義一個遊標 ( GTreeNode
- 遍歷開始前將遊標指向根結點 ( root() )
- 獲取遊標指向的資料元素
- 通過結點中的 child 成員移動遊標
提供一組遍歷相關的函式,按層次訪問樹中的資料元素。

層次遍歷演算法:
- 原料:
class LinkQueue<T>; - 遊標:
LinkQueue<T>: :front(); - 思想:
- begin() → 將根結點壓入佇列中
- current() → 訪問隊頭元素指向的資料元素
- next() → 隊頭元素彈出,將隊頭元素的孩子壓入佇列中 ( 核心 )
- end() → 判斷佇列是否為空
層次遍歷演算法示例:
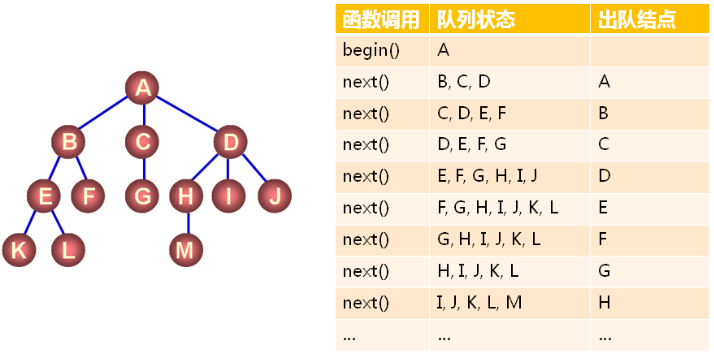
在GTree.h中實現樹形結構的層次遍歷:
protected:
LinkQueue<GTreeNode<T>*> m_queue;
public:
bool begin()
{
bool ret = (root() != NULL);
if( ret )
{
m_queue.clear();
m_queue.add(root());
}
return ret;
}
bool end()
{
return (m_queue.length() == 0);
}
bool next()
{
bool ret = (m_queue.length() > 0);
if( ret )
{
GTreeNode<T>* node = m_queue.front();
m_queue.remove();
for(node->child.move(0); !node->child.end(); node->child.next())
{
m_queue.add(node->child.current());
}
}
return ret;
}
T current()
{
if( !end() )
{
return m_queue.front()->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
}
}然後在其他地方加入對應的清空佇列的程式碼:
public:
SharedPointer< Tree<T> > remove(const T& value)
{
GTree<T>* ret = NULL;
GTreeNode<T>* node = find(value);
if( node == NULL )
{
THROW_EXCEPTION(InvalidParameterException, "Can not find the node via parameter value ...");
}
else
{
remove(node, ret);
m_queue.clear();
}
return ret;
}
SharedPointer< Tree<T> > remove(TreeNode<T>* node)
{
GTree<T>* ret = NULL;
node = find(node);
if( node == NULL )
{
THROW_EXCEPTION(InvalidParameterException, "Parameter node is invalid ...");
}
else
{
remove(dynamic_cast<GTreeNode<T>*>(node), ret);
m_queue.clear();
}
return ret;
}最後把GTree和GTreeNode類的拷貝構造和賦值操作都宣告為保護成員函式:
GTree.h
protected:
GTree(const GTree<T>&);
GTree<T>& operator = (const GTree<T>&);
public:
GTree()
{
}GTreeNode.h
protected:
GTreeNode(const GTreeNode<T>&);
GTreeNode<T>& operator = (const GTreeNode<T>&);最終main.cpp測試
#include <iostream>
#include "GTree.h"
using namespace std;
using namespace StLib;
int main()
{
GTree<char> t;
GTreeNode<char>* node = NULL;
GTreeNode<char> root;
root.value = 'A';
root.parent = NULL;
t.insert(&root);
node = t.find('A');
t.insert('B', node);
t.insert('C', node);
t.insert('D', node);
node = t.find('B');
t.insert('E', node);
t.insert('F', node);
node = t.find('E');
t.insert('K', node);
t.insert('L', node);
node = t.find('C');
t.insert('G', node);
node = t.find('D');
t.insert('H', node);
t.insert('I', node);
t.insert('J', node);
node = t.find('H');
t.insert('M', node);
for(t.begin(); !t.end(); t.next())
{
cout << t.current();
}
cout << endl;
return 0;
}執行結果為:
ABCDEFGHIJKLM3.小結
- 樹的結點沒有固定的編號方式
- 可以按照層次關係對樹中的結點進行遍歷
- 通過遊標的思想設計遍歷成員函式
- 遍歷成員函式是相互依賴,相互配合的關係
- 遍歷演算法的核心為佇列的使用
最終的GTree.h程式碼:
#ifndef GTREE_H
#define GTREE_H
#include "Tree.h"
#include "GTreeNode.h"
#include "Exception.h"
#include "LinkQueue.h"
namespace StLib
{
template <typename T>
class GTree : public Tree<T>
{
protected:
LinkQueue<GTreeNode<T>*> m_queue;
GTree(const GTree<T>&);
GTree<T>& operator = (const GTree<T>&);
GTreeNode<T>* find(GTreeNode<T>* node, const T& value) const
{
GTreeNode<T>* ret = NULL;
if( node != NULL )
{
if( node->value == value )
{
return node;
}
else
{
for(node->child.move(0); !node->child.end() && (ret == NULL); node->child.next())
{
ret = find(node->child.current(), value);
}
}
}
return ret;
}
GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj) const
{
GTreeNode<T>* ret = NULL;
if( node == obj )
{
return node;
}
else
{
if( node != NULL )
{
for(node->child.move(0); !node->child.end() && (ret == NULL); node->child.next())
{
ret = find(node->child.current(), obj);
}
}
}
return ret;
}
void free(GTreeNode<T>* node)
{
if( node != NULL )
{
for(node->child.move(0); !node->child.end(); node->child.next())
{
free(node->child.current());
}
if( node->flag() )
{
delete node;
}
}
}
void remove(GTreeNode<T>* node, GTree<T>*& ret)
{
ret = new GTree<T>();
if( ret == NULL )
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ...");
}
else
{
if( root() == node )
{
this->m_root = NULL;
}
else
{
LinkList<GTreeNode<T>*>& child = dynamic_cast<GTreeNode<T>*>(node->parent)->child;
child.remove(child.find(node));
node->parent = NULL;
}
ret->m_root = node;
}
}
int count(GTreeNode<T>* node) const
{
int ret = 0;
if( node != NULL )
{
ret = 1;
for(node->child.move(0); !node->child.end(); node->child.next())
{
ret += count(node->child.current());
}
}
return ret;
}
int height(GTreeNode<T>* node) const
{
int ret = 0;
if( node != NULL )
{
for(node->child.move(0); !node->child.end(); node->child.next())
{
int h = height(node->child.current());
if( ret < h )
{
ret = h;
}
}
ret = ret + 1;
}
return ret;
}
int degree(GTreeNode<T>* node) const
{
int ret = 0;
if( node != NULL )
{
ret = node->child.length();
for(node->child.move(0); !node->child.end(); node->child.next())
{
int d = degree(node->child.current());
if( ret < d )
{
ret = d;
}
}
}
return ret;
}
public:
GTree()
{
}
bool insert(TreeNode<T>* node)
{
bool ret = true;
if( node != NULL )
{
if( this->m_root == NULL )
{
node->parent = NULL;
this->m_root = node;
}
else
{
GTreeNode<T>* np = find(node->parent);
if( np != NULL )
{
GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node);
if( np->child.find(n) < 0 )
{
np->child.insert(n);
}
}
else
{
THROW_EXCEPTION(InvalidOperationException, "Invalid parent tree node ...");
}
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Parameter node cannot be NULL ...");
}
return ret;
}
bool insert(const T& value, TreeNode<T>* parent)
{
bool ret = true;
GTreeNode<T>* node = GTreeNode<T>::NewNode();
if( node != NULL )
{
node->value = value;
node->parent = parent;
insert(node);
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree node ...");
}
return ret;
}
SharedPointer< Tree<T> > remove(const T& value)
{
GTree<T>* ret = NULL;
GTreeNode<T>* node = find(value);
if( node == NULL )
{
THROW_EXCEPTION(InvalidParameterException, "Can not find the node via parameter value ...");
}
else
{
remove(node, ret);
m_queue.clear();
}
return ret;
}
SharedPointer< Tree<T> > remove(TreeNode<T>* node)
{
GTree<T>* ret = NULL;
node = find(node);
if( node == NULL )
{
THROW_EXCEPTION(InvalidParameterException, "Parameter node is invalid ...");
}
else
{
remove(dynamic_cast<GTreeNode<T>*>(node), ret);
m_queue.clear();
}
return ret;
}
GTreeNode<T>* find(const T& value) const
{
return find(root(), value);
}
GTreeNode<T>* find(TreeNode<T>* node) const
{
return find(root(), dynamic_cast<GTreeNode<T>*>(node));
}
GTreeNode<T>* root() const
{
return dynamic_cast<GTreeNode<T>*>(this->m_root);
}
int degree() const
{
return degree(root());
}
int count() const
{
return count(root());
}
int height() const
{
return height(root());
}
void clear()
{
free(root());
this->m_root = NULL;
m_queue.clear();
}
bool begin()
{
bool ret = (root() != NULL);
if( ret )
{
m_queue.clear();
m_queue.add(root());
}
return ret;
}
bool end()
{
return (m_queue.length() == 0);
}
bool next()
{
bool ret = (m_queue.length() > 0);
if( ret )
{
GTreeNode<T>* node = m_queue.front();
m_queue.remove();
for(node->child.move(0); !node->child.end(); node->child.next())
{
m_queue.add(node->child.current());
}
}
return ret;
}
T current()
{
if( !end() )
{
return m_queue.front()->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
}
}
~GTree()
{
clear();
}
};
}
#endif // GTREE_H