2. 程式人生 > >資料結構開發(24)：二叉樹中屬性操作、層次遍歷與典型遍歷

資料結構開發(24)：二叉樹中屬性操作、層次遍歷與典型遍歷

阿新 • • 發佈：2018-12-23

0.目錄

1.二叉樹中屬性操作的實現

2.二叉樹結構的層次遍歷

3.二叉樹的典型遍歷方式

4.小結

1.二叉樹中屬性操作的實現

二叉樹的屬性操作：

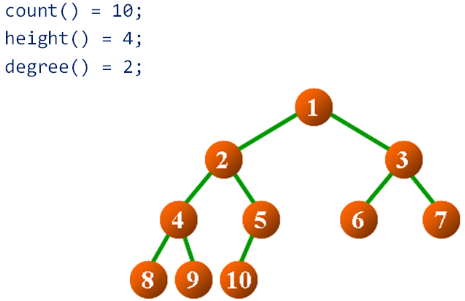
二叉樹中結點的數目：

  • 定義功能：count(node)
    1. 在 node 為根結點的二叉樹中統計結點數目

在BTree.h中實現統計結點數目：

protected:
    int count(BTreeNode<T>* node) const
    {
        int ret = 0;

        if( node != NULL )
        {
            ret = count(node->left) + count(node->right) + 1;
        }

        return ret;
    }
public:
    int count() const
    {
        return count(root());
    }

優化程式碼：

protected:
    int count(BTreeNode<T>* node) const
    {
        return (node != NULL) ? (count(node->left) + count(node->right) + 1) : 0;
    }
public:
    int count() const
    {
        return count(root());
    }

二叉樹的高度：

  • 定義功能：height(node)
    1. 獲取 node 為根結點的二叉樹的高度

在BTree.h中實現獲取二叉樹的高度：

protected:
    int height(BTreeNode<T>* node) const
    {
        int ret = 0;

        if( node != NULL )
        {
            int lh = height(node->left);
            int rh = height(node->right);

            ret = ((lh > rh) ? lh : rh) + 1;
        }

        return ret;
    }
public:
    int height() const
    {
        return height(root());
    }

樹的度數：

  • 定義功能：degree(node)
    1. 獲取 node 為根結點的二叉樹的度數

在BTree.h中實現獲取二叉樹的度數：

protected:
    int degree(BTreeNode<T>* node) const
    {
        int ret = 0;

        if( node != NULL )
        {
            int dl = degree(node->left);
            int dr = degree(node->right);

            ret = (!!node->left + !!node->right);

            if( ret < dl )
            {
                ret = dl;
            }

            if( ret < dr )
            {
                ret = dr;
            }
        }

        return ret;
    }
public:
    int degree() const
    {
        return degree(root());
    }

優化程式碼：

protected:
    int degree(BTreeNode<T>* node) const
    {
        int ret = 0;

        if( node != NULL )
        {
            BTreeNode<T>* child[] = { node->left, node->right };

            ret = (!!node->left + !!node->right);

            for(int i=0; (i<2) && (ret<2); i++)
            {
                int d = degree(child[i]);

                if( ret < d )
                {
                    ret = d;
                }
            }
        }

        return ret;
    }
public:
    int degree() const
    {
        return degree(root());
    }

統一mian.cpp測試：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

int main()
{
    BTree<int> bt;
    BTreeNode<int>* n = NULL;

    bt.insert(1, NULL);

    n = bt.find(1);
    bt.insert(2, n);
    bt.insert(3, n);

    n = bt.find(2);
    bt.insert(4, n);
    bt.insert(5, n);

    n = bt.find(4);
    bt.insert(8, n);
    bt.insert(9, n);

    n = bt.find(5);
    bt.insert(10, n);

    n = bt.find(3);
    bt.insert(6, n);
    bt.insert(7, n);

    cout << bt.count() << endl;
    cout << bt.height() << endl;
    cout << bt.degree() << endl;

    return 0;
}

執行結果為：

10
4
2

2.二叉樹結構的層次遍歷

二叉樹的遍歷：

  • 二叉樹的遍歷 ( Traversing Binay Tree ) 是指從根結點出發，按照某種次序依次訪問二叉樹中的所有結點，使得每個結點被訪問一次，且僅被訪問一次。

需要考慮的問題：

  • 通用樹結構的層次遍歷演算法是否可以用在二叉樹結構上？
  • 如果可以，程式碼需要做怎樣的改動？

設計思路 ( 遊標 )：

  • 提供一組遍歷相關的函式，按層次訪問二叉樹中的資料元素。

層次遍歷演算法：

  • 原料：class LinkQueue
  • 遊標：LinkQueue
  • 思想：
    1. begin() → 將根結點壓入佇列中
    2. current() → 訪問隊頭元素指向的資料元素
    3. next() → 隊頭元素彈出，將隊頭元素的孩子壓入佇列中 ( 核心 )
    4. end() → 判斷佇列是否為空

層次遍歷演算法示例：

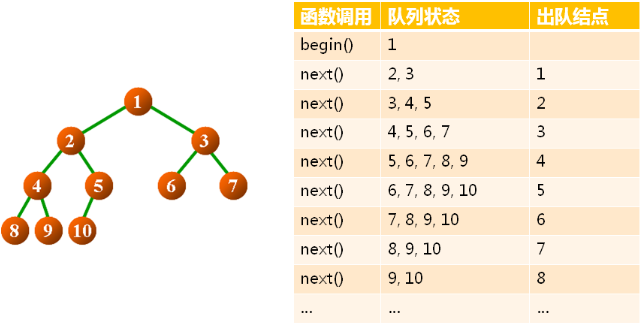
在BTree.h中實現二叉樹結構的層次遍歷：
（並且在clear()函式和remove()函式中要加上清空佇列的操作。另外，將遍歷操作的四個函式在父類中宣告為虛擬函式。）

public:
    bool begin()
    {
        bool ret = (root() != NULL);

        if( ret )
        {
            m_queue.clear();
            m_queue.add(root());
        }

        return ret;
    }

    bool end()
    {
        return (m_queue.length() == 0);
    }

    bool next()
    {
        bool ret = (m_queue.length() > 0);

        if( ret )
        {
            BTreeNode<T>* node = m_queue.front();

            m_queue.remove();

            if( node->left != NULL )
            {
                m_queue.add(node->left);
            }

            if( node->right != NULL )
            {
                m_queue.add(node->right);
            }

        }

        return ret;
    }

    T current()
    {
        if( !end() )
        {
            return m_queue.front()->value;
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
        }
    }

mian.cpp測試：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

int main()
{
    BTree<int> bt;
    BTreeNode<int>* n = NULL;

    bt.insert(1, NULL);

    n = bt.find(1);
    bt.insert(2, n);
    bt.insert(3, n);

    n = bt.find(2);
    bt.insert(4, n);
    bt.insert(5, n);

    n = bt.find(4);
    bt.insert(8, n);
    bt.insert(9, n);

    n = bt.find(5);
    bt.insert(10, n);

    n = bt.find(3);
    bt.insert(6, n);
    bt.insert(7, n);

    for(bt.begin(); !bt.end(); bt.next())
    {
        cout << bt.current() << " ";
    }

    cout << endl;

    return 0;
}

執行結果為：

1 2 3 4 5 6 7 8 9 10

3.二叉樹的典型遍歷方式

問題：

  • 二叉樹是否只有一種遍歷方式 ( 層次遍歷 ) ？

典型的二叉樹遍歷方式：

  • 先序遍歷 ( Pre-Order Traversal )
  • 中序遍歷 ( In-Order Traversal )
  • 後序遍歷 ( Post-Order Traversal )

先序遍歷 ( Pre-Order Traversal )：

  • 二叉樹為空：
    1. 無操作，直接返回
  • 二叉樹不為空：
    1. 訪問根結點中的資料元素
    2. 先序遍歷左子樹
    3. 先序遍歷右子樹

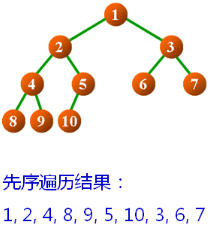
先序遍歷功能定義：

中序遍歷 ( In-Order Traversal )：

  • 二叉樹為空：
    1. 無操作，直接返回
  • 二叉樹不為空：
    1. 中序遍歷左子樹
    2. 訪問根結點中的資料元素
    3. 中序遍歷右子樹

中序遍歷功能定義：

後序遍歷 ( Post-Order Traversal )：

  • 二叉樹為空：
    1. 無操作，直接返回
  • 二叉樹不為空：
    1. 後序遍歷左子樹
    2. 後序遍歷右子樹
    3. 訪問根結點中的資料元素

後序遍歷功能定義：

需要考慮的問題：

  • 是否可以將二叉樹的典型遍歷演算法整合到 BTree 中？
  • 如果可以，程式碼需要做怎樣的改動？

設計要點：

  • 不能與層次遍歷函式衝突，必須設計新的函式介面
  • 演算法執行完成後，能夠方便的獲得遍歷結果
  • 遍歷結果能夠反映結點訪問的先後次序

函式介面設計

  • SharedPointer< Array<T> > traversal(BTTraversal order)
    1. 根據引數 order 選擇執行遍歷演算法 ( 先序，中序，後序 )
    2. 返回值為堆中的陣列物件 ( 生命期由智慧指標管理 )
    3. 陣列元素的次序反映遍歷的先後次序

典型遍歷示例：

二叉樹的典型遍歷方式：

#include "LinkQueue.h"
#include "DynamicArray.h"
namespace StLib
{

enum BTTraversal
{
    PreOrder,
    InOrder,
    PostOrder
};

template <typename T>
class BTree : public Tree<T>
{
protected:
    void preOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
    {
        if( node != NULL )
        {
            queue.add(node);
            preOrderTraversal(node->left, queue);
            preOrderTraversal(node->right, queue);
        }
    }

    void inOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
    {
        if( node != NULL )
        {
            inOrderTraversal(node->left, queue);
            queue.add(node);
            inOrderTraversal(node->right, queue);
        }
    }

    void postOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
    {
        if( node != NULL )
        {
            postOrderTraversal(node->left, queue);
            postOrderTraversal(node->right, queue);
            queue.add(node);
        }
    }
public:
    SharedPointer< Array<T> > traversal(BTTraversal order)
    {
        DynamicArray<T>* ret = NULL;
        LinkQueue<BTreeNode<T>*> queue;

        switch (order) {
        case PreOrder:
            preOrderTraversal(root(), queue);
            break;
        case InOrder:
            inOrderTraversal(root(), queue);
            break;
        case PostOrder:
            postOrderTraversal(root(), queue);
            break;
        default:
            THROW_EXCEPTION(InvalidParameterException, "Parameter order is invalid ...");
            break;
        }

        ret = new DynamicArray<T>(queue.length());

        if( ret != NULL )
        {
            for(int i=0; i<ret->length(); i++, queue.remove())
            {
                ret->set(i, queue.front()->value);
            }
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create return array ...");
        }

        return ret;
    }
};

}

main.cpp測試：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

int main()
{
    BTree<int> bt;
    BTreeNode<int>* n = NULL;

    bt.insert(1, NULL);

    n = bt.find(1);
    bt.insert(2, n);
    bt.insert(3, n);

    n = bt.find(2);
    bt.insert(4, n);
    bt.insert(5, n);

    n = bt.find(4);
    bt.insert(8, n);
    bt.insert(9, n);

    n = bt.find(5);
    bt.insert(10, n);

    n = bt.find(3);
    bt.insert(6, n);
    bt.insert(7, n);

    cout << bt.count() << endl;
    cout << bt.height() << endl;
    cout << bt.degree() << endl;

    cout << "層次遍歷：" << endl;
    for(bt.begin(); !bt.end(); bt.next())
    {
        cout << bt.current() << " ";
    }
    cout << endl;

    SharedPointer< Array<int> > sp = NULL;

    sp = bt.traversal(PreOrder);

    cout << "先序遍歷：" << endl;
    for(int i=0; i<(*sp).length(); i++)
    {
        cout << (*sp)[i] << " ";
    }
    cout << endl;

    sp = bt.traversal(InOrder);

    cout << "中序遍歷：" << endl;
    for(int i=0; i<(*sp).length(); i++)
    {
        cout << (*sp)[i] << " ";
    }
    cout << endl;

    sp = bt.traversal(PostOrder);

    cout << "後序遍歷：" << endl;
    for(int i=0; i<(*sp).length(); i++)
    {
        cout << (*sp)[i] << " ";
    }
    cout << endl;

    return 0;
}

執行結果為：

10
4
2
層次遍歷：
1 2 3 4 5 6 7 8 9 10 
先序遍歷：
1 2 4 8 9 5 10 3 6 7 
中序遍歷：
8 4 9 2 10 5 1 6 3 7 
後序遍歷：
8 9 4 10 5 2 6 7 3 1

4.小結

  • 二叉樹的典型遍歷都是以遞迴方式執行的
  • BTree 以不同的函式介面支援典型遍歷
  • 層次遍歷與典型遍歷互不衝突
  • 遍歷結果能夠反映樹結點訪問的先後次序

最終的BTree.h程式碼：
BTree.h

#ifndef BTREE_H
#define BTREE_H

#include "Tree.h"
#include "BTreeNode.h"
#include "Exception.h"
#include "LinkQueue.h"
#include "DynamicArray.h"

namespace StLib
{

enum BTTraversal
{
    PreOrder,
    InOrder,
    PostOrder
};

template <typename T>
class BTree : public Tree<T>
{
protected:
    LinkQueue<BTreeNode<T>*> m_queue;

    virtual BTreeNode<T>* find(BTreeNode<T>* node, const T& value) const
    {
        BTreeNode<T>* ret = NULL;

        if( node != NULL )
        {
            if( node->value == value )
            {
                return node;
            }
            else
            {
                if( ret == NULL )
                {
                    ret = find(node->left, value);
                }

                if( ret == NULL )
                {
                    ret = find(node->right, value);
                }
            }
        }

        return ret;
    }

    virtual BTreeNode<T>* find(BTreeNode<T>* node, BTreeNode<T>* obj) const
    {
        BTreeNode<T>* ret = NULL;

        if( node == obj )
        {
            return node;
        }
        else
        {
            if( node != NULL )
            {
                if( ret == NULL )
                {
                    ret = find(node->left, obj);
                }

                if( ret == NULL )
                {
                    ret = find(node->right, obj);
                }
            }
        }

        return ret;
    }

    virtual bool insert(BTreeNode<T>* n, BTreeNode<T>* np, BTNodePos pos)
    {
        bool ret = true;

        if( pos == ANY )
        {
            if( np->left == NULL )
            {
                np->left = n;
            }
            else if( np->right == NULL )
            {
                np->right = n;
            }
            else
            {
                ret = false;
            }
        }
        else if( pos == LEFT )
        {
            if( np->left == NULL )
            {
                np->left = n;
            }
            else
            {
                ret = false;
            }
        }
        else if( pos == RIGHT )
        {
            if( np->right == NULL )
            {
                np->right = n;
            }
            else
            {
                ret = false;
            }
        }
        else
        {
            ret = false;
        }

        return ret;
    }

    virtual void remove(BTreeNode<T>* node, BTree<T>*& ret)
    {
        ret = new BTree<T>();

        if( ret == NULL )
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ...");
        }
        else
        {
            if( root() == node )
            {
                this->m_root = NULL;
            }
            else
            {
                BTreeNode<T>* parent = dynamic_cast<BTreeNode<T>*>(node->parent);

                if( parent->left == node )
                {
                    parent->left = NULL;
                }
                else if( parent->right == node )
                {
                    parent->right = NULL;
                }

                node->parent = NULL;
            }

            ret->m_root = node;
        }
    }

    virtual void free(BTreeNode<T>* node)
    {
        if( node != NULL )
        {
            free(node->left);
            free(node->right);

            if( node->flag() )
            {
                delete node;
            }
        }
    }

    int count(BTreeNode<T>* node) const
    {
        return (node != NULL) ? (count(node->left) + count(node->right) + 1) : 0;
    }

    int height(BTreeNode<T>* node) const
    {
        int ret = 0;

        if( node != NULL )
        {
            int lh = height(node->left);
            int rh = height(node->right);

            ret = ((lh > rh) ? lh : rh) + 1;
        }

        return ret;
    }

    int degree(BTreeNode<T>* node) const
    {
        int ret = 0;

        if( node != NULL )
        {
            BTreeNode<T>* child[] = { node->left, node->right };

            ret = (!!node->left + !!node->right);

            for(int i=0; (i<2) && (ret<2); i++)
            {
                int d = degree(child[i]);

                if( ret < d )
                {
                    ret = d;
                }
            }
        }

        return ret;
    }

    void preOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
    {
        if( node != NULL )
        {
            queue.add(node);
            preOrderTraversal(node->left, queue);
            preOrderTraversal(node->right, queue);
        }
    }

    void inOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
    {
        if( node != NULL )
        {
            inOrderTraversal(node->left, queue);
            queue.add(node);
            inOrderTraversal(node->right, queue);
        }
    }

    void postOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
    {
        if( node != NULL )
        {
            postOrderTraversal(node->left, queue);
            postOrderTraversal(node->right, queue);
            queue.add(node);
        }
    }
public:
    bool insert(TreeNode<T>* node)
    {
        return insert(node, ANY);
    }

    virtual bool insert(TreeNode<T>* node, BTNodePos pos)
    {
        bool ret = true;

        if( node != NULL )
        {
            if( this->m_root == NULL )
            {
                node->parent = NULL;
                this->m_root = node;
            }
            else
            {
                BTreeNode<T>* np = find(node->parent);

                if( np != NULL )
                {
                    ret = insert(dynamic_cast<BTreeNode<T>*>(node), np, pos);
                }
                else
                {
                    THROW_EXCEPTION(InvalidParameterException, "Invalid parent tree node ...");
                }
            }
        }
        else
        {
            THROW_EXCEPTION(InvalidParameterException, "Parameter node can not be NULL ...");
        }

        return ret;
    }

    bool insert(const T& value, TreeNode<T>* parent)
    {
        return insert(value, parent, ANY);
    }

    virtual bool insert(const T& value, TreeNode<T>* parent, BTNodePos pos)
    {
        bool ret = true;
        BTreeNode<T>* node = BTreeNode<T>::NewNode();

        if( node == NULL )
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new node ...");
        }
        else
        {
            node->value = value;
            node->parent = parent;

            ret = insert(node, pos);

            if( !ret )
            {
                delete node;
            }
        }

        return ret;
    }

    SharedPointer< Tree<T> > remove(const T& value)
    {
        BTree<T>* ret = NULL;
        BTreeNode<T>* node = find(value);

        if( node == NULL )
        {
            THROW_EXCEPTION(InvalidParameterException, "Can not find the tree node via value ...");
        }
        else
        {
            remove(node, ret);

            m_queue.clear();
        }

        return ret;
    }

    SharedPointer< Tree<T> > remove(TreeNode<T>* node)
    {
        BTree<T>* ret = NULL;

        node = find(node);

        if( node == NULL )
        {
            THROW_EXCEPTION(InvalidParameterException, "Parameter node is invalid ...");
        }
        else
        {
            remove(dynamic_cast<BTreeNode<T>*>(node), ret);

            m_queue.clear();
        }

        return ret;
    }

    BTreeNode<T>* find(const T& value) const
    {
        return find(root(), value);
    }

    BTreeNode<T>* find(TreeNode<T>* node) const
    {
        return find(root(), dynamic_cast<BTreeNode<T>*>(node));
    }

    BTreeNode<T>* root() const
    {
        return dynamic_cast<BTreeNode<T>*>(this->m_root);
    }

    int degree() const
    {
        return degree(root());
    }

    int count() const
    {
        return count(root());
    }

    int height() const
    {
        return height(root());
    }

    void clear()
    {
        free(root());

        m_queue.clear();

        this->m_root = NULL;
    }

    bool begin()
    {
        bool ret = (root() != NULL);

        if( ret )
        {
            m_queue.clear();
            m_queue.add(root());
        }

        return ret;
    }

    bool end()
    {
        return (m_queue.length() == 0);
    }

    bool next()
    {
        bool ret = (m_queue.length() > 0);

        if( ret )
        {
            BTreeNode<T>* node = m_queue.front();

            m_queue.remove();

            if( node->left != NULL )
            {
                m_queue.add(node->left);
            }

            if( node->right != NULL )
            {
                m_queue.add(node->right);
            }

        }

        return ret;
    }

    T current()
    {
        if( !end() )
        {
            return m_queue.front()->value;
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
        }
    }

    SharedPointer< Array<T> > traversal(BTTraversal order)
    {
        DynamicArray<T>* ret = NULL;
        LinkQueue<BTreeNode<T>*> queue;

        switch (order) {
        case PreOrder:
            preOrderTraversal(root(), queue);
            break;
        case InOrder:
            inOrderTraversal(root(), queue);
            break;
        case PostOrder:
            postOrderTraversal(root(), queue);
            break;
        default:
            THROW_EXCEPTION(InvalidParameterException, "Parameter order is invalid ...");
            break;
        }

        ret = new DynamicArray<T>(queue.length());

        if( ret != NULL )
        {
            for(int i=0; i<ret->length(); i++, queue.remove())
            {
                ret->set(i, queue.front()->value);
            }
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create return array ...");
        }

        return ret;
    }

    ~BTree()
    {
        clear();
    }
};

}

#endif // BTREE_H

相關推薦

資料結構開發(24)：二叉樹中屬性操作、層次遍歷與典型遍歷

0.目錄 1.二叉樹中屬性操作的實現 2.二叉樹結構的層次遍歷 3.二叉樹的典型遍歷方式 4.小結 1.二叉樹中屬性操作的實現 二叉樹的屬性操作： 二叉樹中結點的數目： 定義功能：count(node) 在 node 為根結點的二叉樹中統計結點數目 在

資料結構開發(25)：二叉樹中屬性操作、層次遍歷與典型遍歷

0.目錄 1.二叉樹的比較與相加 2.二叉樹的線索化實現 3.二叉樹的經典面試題分析 3.1 單度結點刪除 3.2 中序線索化二叉樹 4.小結 1.二叉樹的比較與相加 二叉樹的克隆操作： SharedPointer< BTree<T> > clone

資料結構開發(23)：二叉樹中結點的查詢、插入、刪除與清除操作

0.目錄 1.二叉樹中結點的查詢操作 2.二叉樹中結點的插入操作 3.二叉樹中結點的刪除操作 4.二叉樹中結點的清除操作 5.小結 1.二叉樹中結點的查詢操作 查詢的方式： 基於資料元素值的查詢 BTreeNode<T>* find(const T&

資料結構 筆記：二叉樹中屬性操作的實現

二叉樹的屬性操作 count() = 10; height() = 4; degree() = 2; 二叉樹結點的數目 -定義功能：count(node) ·在node為根結點的二叉樹中統計結點數目 int count(BTreeNode<T>* nod

數據結構開發(22)：二叉樹的轉換、深層特性與存儲結構設計

his 9.png 二叉 klist efi remove ren binary 兩個 0.目錄 1.樹到二叉樹的轉換 2.二叉樹的深層特性 3.二叉樹的存儲結構設計 4.小結 1.樹到二叉樹的轉換 通用樹結構的回顧： 雙親孩子表示法 每個結點都有一個指向其雙親的指針

資料結構和演算法：二叉樹

二叉樹 二叉樹（Binary tree）是樹形結構的一個重要型別。許多實際問題抽象出來的資料結構往往是二叉樹形式，即使是一般的樹也能簡單地轉換為二叉樹，而且二叉樹的儲存結構及其演算法都較為簡單，因此二叉樹顯得特別重要。二叉樹特點是每個節點最多隻能有兩棵子樹，即樹的度最大為2，且有左右之分 。 二叉樹是n個有限

資料結構實驗3《二叉樹的基本操作》

根據輸入的資料建立一個二叉樹；分別採用前序、中序、後序的遍歷方式顯示輸出二叉樹的遍歷結果程式碼：#include<iostream> using namespace std; struct

資料結構 筆記：二叉樹中的結點刪除與清除

刪除的方式 -基於資料元素值的刪除 ·SharedPointer<Tree<T>>remove(const T& value) -基於結點的刪除 ·SharedPointer<Tree <T>>remove(TreeNode&l

資料結構 筆記：二叉樹中的結點插入操作

是否能夠在二叉樹的而已結點出插入子結點？ -不能，二叉樹結點的每個結點的子結點是固定的，只存在左孩子和右孩子. 是否需要指定新資料元素（新結點）的插入位置？ -需要指定為左孩子或者右孩子 enum BTNodePos { ANY, LEFT, RIGHT };

資料結構 筆記：二叉樹中的結點查詢操作

查詢的方式 -基於資料元素值的查詢 ·BTreeNode<T>* find(const T& value) const -基於結點的查詢 ·BTreeNode<T>* find(TreeNode<T>* node) const 基於資料

【資料結構】BST：二叉排序樹演算法

建立二叉排序樹，實現樹的插入、刪除，前、中、後序遍歷（遞迴方式）等操作。 /***************************************** Copyright (c) 2015 Jingshuang Hu @filename:dem

基本數據結構學習總結： 二叉樹的遍歷

root 取出 後序 二叉 isnull 就是 bre 遞歸 use 二叉搜索樹的遍歷 二叉樹遍歷的內容很多，但是也是最重要的，最需要理解的，很多二叉樹的相關算法，只要用活了遍歷就沒有問題了 前序遍歷 對於每一棵樹，先遍歷其根節點，然後遍歷其左子樹，最後用同樣的方式遍歷

資料結構——4.2 平衡二叉樹

搜尋樹結點不同的插入次序，將導致不同的深度和平均查詢長度ASL 平衡因子：BF（T）=hL-hR，其中hL和hR分別為T的左右子樹的高度。 平衡二叉樹（AVL樹）：是一個空樹或者 要求任一結點左右子樹高度差的絕對值小於等於1，即|BF(T)| <=1 設nh為 高度是h

資料結構之－平衡二叉樹(AVL)

背景 不同結構的二叉查詢樹，查詢效率有很大的不同。如何解決這個問題呢？關鍵在於如何最大限度的減小樹的深度。正是基於這個想法，平衡二叉樹出現了。 前言 平衡二叉搜尋樹（英語：Balanced Binary Tree）是一種結構平衡的二叉搜尋樹。 它能在O(log n)時間內完成插入、查詢和

【資料結構】3-1 二叉樹的先序建立及遍歷操作

二叉樹真的令人頭大 #include<iostream> using namespace std; template <class T> struct BTNode//二叉連結串列結點結構 { T data; //二叉樹中的元素 BTNode<T>

資料結構——鏈佇列實現二叉樹的層次遍歷

在二叉樹的遍歷這篇部落格中https://www.cnblogs.com/wkfvawl/p/9901462.html 對於二叉樹的層次遍歷我只是給出了基於C++ STL的程式碼，這裡我使用資料結構的連結串列，構建一個鏈佇列來實現。這也算是我第一次使用鏈佇列來完成某個任務，鏈佇列程式碼還是來自課本，因為之前

資料結構實驗-C語言-二叉樹的建立，前、中、後序遍歷的遞迴演算法和非遞迴演算法，求葉子結點數目，求二叉樹深度，判斷二叉樹是否相似，求二叉樹左右子樹互換，二叉樹層序遍歷的演算法，判斷二叉樹是否是完全二叉樹

1.實驗目的 熟練掌握二叉樹的二叉連結串列儲存結構的C語言實現。掌握二叉樹的基本操作-前序、中序、後序遍歷二叉樹的三種方法。瞭解非遞迴遍歷過程中“棧”的作用和狀態，而且能靈活運用遍歷演算法實現二叉樹的其它操作。 2.實驗內容 （1）二叉樹的二叉連結串列的建立 （2）二叉樹的前、中、後

劍指offer-24：二叉樹中和為某一值的路徑

題目描述 輸入一顆二叉樹的根節點和一個整數，打印出二叉樹中結點值的和為輸入整數的所有路徑。路徑定義為從樹的根結點開始往下一直到葉結點所經過的結點形成一條路徑。(注意: 在返回值的list中，陣列長度大的陣列靠前) 思路 dfs演算法 程式碼 public class So

C語言複習資料結構之簡單的二叉樹輸入和輸出操作

C語言複習之簡單的二叉樹的僅輸入輸出操作 1：結構體 typedef struct TreeNode{ _Data value; struct TreeNode * father; struct TreeNode * right; stru

【資料結構學習筆記】二叉樹和其他樹

基礎定義 一個樹t是一個非空的有限元素的集合，其中一個元素為根（root），其餘的元素（如果有的話）組成t的子樹（subtree） 樹的另一常用術語為級（level）。樹根是1級，其孩子（如果有）是2級，孩子的孩子是3級，等等。 一棵樹的高度（height）或深度（de