前記

演算法流程

1 初始化最小堆q,距離陣列dist全為無窮大，collected陣列為全0，path陣列全為-1，dist[i]代表頂點i到源頂點的最短距離，最小堆按照dist的大小進行排序，源頂點為s,dist[s]=0。源頂點s加入最小堆。Collected[i]代表頂點i是否加入最小堆，0代表未收錄，1代表收錄。path[i]代表頂點i最短路徑上的中間頂點，其中-1代表源頂點。
2 從最小堆中彈出堆頂元素start，之後遍歷（bfs）相鄰結點i，若start和i之間的權重G[start][i]+dist[start]<dist[i],那麼dist[i]=G[start][i]+dist[start]。並且將i加入最小堆。
3 最小堆不為空時，迴圈執行步驟2

C++程式碼

#include <iostream>
#include <cstring>
#include <stack>
#include <queue> 
#include <vector> 
using namespace std;

const int MAX = 65535;
int G[1001][1001];
int dist[1001] = {0};
int path[1001] = {0};
int visited[1001] = {0};
int Nv,Ne;
int start;

struct cmp{
	bool operator()(int &a,int &b){
		return dist[a]>dist[b];
	}
};

void Create_Graph()
{
	//初始化距離陣列為正無窮 
	for(int i = 0 ; i < 1001 ; i++){
		dist[i] = MAX;
	}
	//初始化路徑陣列為-1 
	memset(path,-1,sizeof(path[0])*(1001));
	//初始化訪問陣列為-1 
	memset(visited,0,sizeof(visited[0])*(1001));
	//memset(this->collected,0,sizeof(this->collected[0])*(nv+1));
	for(int i = 0 ; i < 1001 ; i++){
		for(int j = 0 ; j < 1001 ; j++){
			G[i][j] = MAX;	
		}
	}
	//初始化圖
	cout<<"請輸入頂點數與邊數："<<endl; 
	cin>>Nv>>Ne;
	cout<<"請輸入邊與權重："<<endl;
	for(int i = 0 ; i < Ne ; i++){
		int v1,v2,weight;
		cin>>v1>>v2>>weight;
		G[v1][v2] = G[v2][v1] = weight;
	}	
}

//迪傑斯特拉演算法 
bool Dijikstra(int vertex)
{
	priority_queue<int,vector<int>,cmp> q;
	//源頂點加入最小堆 
	q.push(vertex);
	//初始化源頂點的dist為0 
	dist[vertex] = 0;
	visited[vertex] = 1; 
	//最小堆不為空，一直迴圈 
	while(!q.empty()){
		//從最小堆中彈出最小元素 
		int start = q.top();
		q.pop();
		for(int i = 1 ; i < Nv+1 ; i++){
			//負值圈問題 
			if(G[start][i] < 0){
				return false;
			}
			// bfs遍歷領接結點 
			if (G[start][i] < MAX){
				if(visited[i] == 0){
					// i到start的最小距離大於dist[start]+G[start][i]
					if(dist[i] > dist[start] + G[start][i]){
						dist[i] = dist[start] + G[start][i];
						q.push(i);
						path[i] = start;
					}	
				}	
			}
		}
	}
	return true;
}

//列印start到end的最短路徑 
void Print(int start ,int end)
{
	stack<int> stack;
	stack.push(end);
	cout<<start<<"到"<<end<<"的最短路徑為：";
	int j = end;
	while(path[j] != -1){//路徑上的元素一次入棧 
		j = path[j];
		stack.push(j);	
	}
	//列印路徑 
	cout<<stack.top();
	stack.pop(); 
	while(!stack.empty()){
	cout<<" -> "<<stack.top();
	stack.pop();
	}
	cout<<"\n"<<"最短路徑長度為："<<dist[end]<<endl;
}

void Print_Dijikstra(int vertex)
{
	for(int i = 1 ; i < Nv+1 ; i++){
		if(i == vertex){
			continue;
		} 
		Print(vertex,i); 
	}
}


int main() 
{
	Create_Graph();
	cout<<"請輸入一個起始點："<<endl;
	int vertex;
	cin>>vertex;
	if(Dijikstra(vertex)){
		Print_Dijikstra(vertex); 	
	}
	
	return 0;
}
 

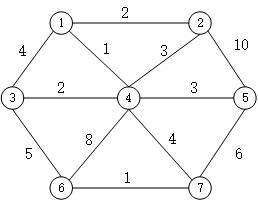
例子