2.1  關係資料結構及形式化定義

2.1.1  關係

1. 域（Domain）：是一組具有相同資料型別的值的集合。

 2. 笛卡爾積（Cartesian Product）

（1）

• 給定一組域D1，D2，…，Dn，允許其中某些域是相同的。

    D1，D2，…，Dn的笛卡爾積為：

    D1×D2×…×Dn ＝        

｛（d1，d2，…，dn）｜diÎDi，i＝1，2，…，n｝

• 所有域的所有取值的一個組合
• 不能重複

（2）元組（Tuple）

n笛卡爾積中每一個元素（d1，d2，…，dn）叫作一個n元組（n-tuple）或簡稱元組

n(張清玫，計算機專業，李勇

)、  (張清玫，計算機專業，劉晨)  等 都是元組   

（3）分量（Component）

n笛卡爾積元素（d1，d2，…，dn）中的每一個值di 叫作一個分量

n張清玫、計算機專業、李勇、劉晨等都是分量

（4）基數（Cardinal number）

n若Di（i＝1，2，…，n）為有限集，其基數為mi（i＝1，2，…，n），則D1×D2×…×Dn的基數M為：

（5）笛卡爾積的表示方法

n笛卡爾積可表示為一張二維表

n表中的每行對應一個元組，表中的每列對應一個域

例如，給出3個域：

D1=導師集合SUPERVISOR=｛張清玫，劉逸｝

D2=專業集合SPECIALITY=

｛計算機專業，資訊專業｝

D3=研究生集合POSTGRADUATE=｛李勇，劉晨，王敏｝

vD1，D2，D3的笛卡爾積為

vD1×D2×D3＝｛

        (張清玫，計算機專業，李勇)，(張清玫，計算機專業，劉晨)，

        (張清玫，計算機專業，王敏)，(張清玫，資訊專業，李勇)，

        (張清玫，資訊專業，劉晨)，(張清玫，資訊專業，王敏)，

        (劉逸，計算機專業，李勇)，(劉逸，計算機專業，劉晨)，

        (劉逸，計算機專業，王敏)，(劉逸，資訊專業，李勇)，

        (劉逸，資訊專業，劉晨)，(劉逸，資訊專業，王敏

) ｝

v基數為2×2×3＝12

 3. 關係（Relation）

（1） 關係

D1×D2×…×Dn的子集叫作在域D1，D2，…，Dn上的

關係，表示為

         R（D1，D2，…，Dn）

• R：關係名
• n：關係的目或度（Degree）

（2）元組：關係中的每個元素是關係中的元組，通常用t表示。

（3）單元關係與二元關係

當n=1時，稱該關係為單元關係（Unary relation）或一元關係                            

當n=2時，稱該關係為二元關係（Binary relation）

（4）關係的表示：關係也是一個二維表，表的每行對應一個元組，表的每列對應一個域

（5）屬性

• 關係中不同列可以對應相同的域

為了加以區分，必須對每列起一個名字，稱為屬性（Attribute）

• n目關係必有n個屬性

（6）碼

候選碼（Candidate key）

    若關係中的某一屬性組的值能唯一地標識一個元組，則稱該屬性組為候選碼

    簡單的情況：候選碼只包含一個屬性

全碼（All-key）

最極端的情況：關係模式的所有屬性組是這個關係模式的候選碼，稱為全碼（All-key）

主碼

若一個關係有多個候選碼，則選定其中一個為主碼（Primary key）

主屬性

候選碼的諸屬性稱為主屬性（Prime attribute） 

不包含在任何侯選碼中的屬性稱為非主屬性（Non-Prime attribute）或非碼屬性（Non-key attribute）

（7）三類關係

基本關係（基本表或基表）：實際存在的表，是實際儲存資料的邏輯表示

查詢表：查詢結果對應的

視圖表：由基本表或其他視圖表匯出的表，是虛表，不對應實際儲存的資料

（8）基本關係的性質

① 列是同質的（Homogeneous）

② 不同的列可出自同一個域,l其中的每一列稱為一個屬性,不同的屬性要給予不同的屬性名

③ 列的順序無所謂,，列的次序可以任意交換

④ 任意兩個元組的候選碼不能相同

⑤ 行的順序無所謂，行的次序可以任意交換

2.1.2  關係模式

1．什麼是關係模式

v關係模式（Relation Schema）是型

v關係是值

v關係模式是對關係的描述

2．定義關係模式

(1)關係模式可以形式化地表示為：

      R（U，D，DOM，F）

  R              關係名

  U              組成該關係的屬性名集合

  D              U中屬性所來自的域

  DOM         屬性向域的映象集合

  F               屬性間資料的依賴關係的集合

(2)關係模式通常可以簡記為

   R (U)    或    R (A1，A2，…，An)

R: 關係名

A1，A2，…，An  : 屬性名

注：域名及屬性向域的映象常常直接說明為屬性的型別、長度

2.2  關係操作

（1）常用的關係操作

n查詢操作：選擇、投影、連線、除、並、差、交、笛卡爾積

•    選擇、投影、並、差、笛卡爾基是5種基本操作

n資料更新：插入、刪除、修改

（2）關係代數語言：用對關係的運算來表達查詢要求

（3）關係演算語言：用謂詞來表達查詢要求

（4）具有關係代數和關係演算雙重特點的語言：代表：SQL（Structured Query Language）

2.3  關係的完整性

2.3.1 實體完整性

• 基本關係R的主屬性不能取空值
• 空值就是“不知道”或“不存在”或“無意義”的值

     例：

選修（學號，課程號，成績）

“學號、課程號”為主碼

“學號”和“課程號”兩個屬性都不能取空值

2.3.2 參照完整性

1. 外碼

v設F是基本關係R的一個或一組屬性，但不是關係R的碼。如果F與基本關係S的主碼Ks相對應，則稱F是R的外碼

v基本關係R稱為參照關係（Referencing  Relation）

v基本關係S稱為被參照關係（Referenced Relation） 或目標關係（Target Relation）

例：

選修關係的“學號” 與學生關係的主碼“學號”相對應

選修關係的“課程號”與課程關係的主碼“課程號”相對應

n“學號”和“課程號”是選修關係的外碼

n學生關係和課程關係均為被參照關係

選修關係為參照關係

2. 參照完整性規則

若屬性（或屬性組）F是基本關係R的外碼它與基本關係S的主碼Ks相對應（基本關係R和S不一定是不同的關係），則對於R中每個元組在F上的值必須為：

• 或者取空值（F的每個屬性值均為空值）
• 或者等於S中某個元組的主碼值

2.3.3 使用者定義的完整性

v針對某一具體關係資料庫的約束條件，反映某一具體應用所涉及的資料必須滿足的語義要求

2.4  關係代數

v關係代數是一種抽象的查詢語言，它用對關係的運算來表達查詢

關係代數運算子

運　算　符		含　義
集合 運算子	∪	並
	-	差
	∩	交
	×	笛卡爾積
專門的 關係 運算子	σ	選擇
	π	投影
		連線
	÷	除

2.4.1 傳統的集合運算

（1）並  R∪S

由屬於R或屬於S的元組組成（①R和S具有相同的目n（即兩個關係都有n個屬性）②相應的屬性取自同一個域）

          

（2）差 R - S

由屬於R而不屬於S的所有元組組成（①R和S具有相同的目n（即兩個關係都有n個屬性）②相應的屬性取自同一個域）

               

（3）交 R∩S

由既屬於R又屬於S的元組組成

（4）笛卡爾積

R: n目關係，k1個元組

S: m目關係，k2個元組

R×S

①列：（n+m）列元組的集合

元組的前n列是關係R的一個元組

後m列是關係S的一個元組

②行：k1×k2個元組

例項： 

          

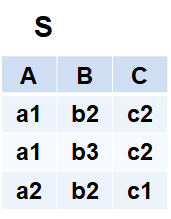
 2.4.2 專門的關係運算

引入：象集Zx

  給定一個關係R（X，Z），X和Z為屬性組。

  當t[X]=x時，x在R中的象集（Images Set）為：

      它表示R中屬性組X上值為x的諸元組在Z上分量的集合

舉例：            

1. 選擇

選擇運算子的含義：

                              在關係R中選擇滿足給定條件的諸元組 

         

             ①F：選擇條件，是一個邏輯表示式，取值為“真”或“假”

             ②基本形式為：X1θY1（θ表示比較運算子，它可以是＞，≥，＜，≤，＝或<>）

選擇運算是從關係R中選取使邏輯表示式F為真的元組，是從行的角度進行的運算

2. 投影：從R中選擇出若干屬性列組成新的關係

           投影操作主要是從列的角度進行運算，投影之後不僅取消了原關係中的某些列，而且還可能取消某些元組（避免重複行）

 

3. 連線（也稱為θ連線）

（1）連線運算的含義

從兩個關係的笛卡爾積中選取屬性間滿足一定條件的元組

①A和B：分別為R和S上度數相等且可比的屬性組   ②θ：比較運算子  

連線運算從R和S的廣義笛卡爾積R×S中選取R關係在A屬性組上的值與S關係在B屬性組上的值滿足比較關係θ的元組

（2）兩類常用連線運算

Ⅰ  等值連線（equijoin） ：θ為“＝”的連線運算稱為等值連線

從關係R與S的廣義笛卡爾積中選取A、B屬性值相等的那些元組，即等值連線為：

Ⅱ   自然連線（Natural join） （自然連線是一種特殊的等值連線）

Ø兩個關係中進行比較的分量必須是相同的屬性組

Ø在結果中把重複的屬性列去掉

                           自然連線的含義：R和S具有相同的屬性組B

     

例項： 

一般連線： 

           兩個關係先做笛卡爾積，然後從中挑選出符合要求的元組。

等值連線和自然連線： 

  

 （3）懸浮元組（Dangling tuple）

兩個關係R和S在做自然連線時，關係R中某些元組有可能在S中不存在公共屬性上值相等的元組，從而造成R中這些元組在操作時被捨棄了