【演算法】聚類和分類
目錄
一、聚類和分類的區別
簡單的說,聚類的分析沒有學習集,而分類有學習集

二、常用聚類演算法
1.動態聚類:K-means方法
演算法步驟:
1.選擇K個點作為初始質心
2.將每個點指派到最近的質心,形成K個簇(聚類)
3.重新計算每個簇的質心 4 重複2-3直至質心不發生變化
K-means演算法的優缺點:
1.有效率,而且不容易受初始值選擇的影響
2.不能處理非球形的簇
3.不能處理不同尺寸,不同密度的簇
4.離群值可能有較大幹擾(因此要先剔除)
2.基於有代表性的點的技術:K中心聚類法
演算法步驟:
1. 隨機選擇k個點作為“中心點”
2 .計算剩餘的點到這k箇中心點的距離,每個點被分配到最近的中心點組成聚簇
3. 隨機選擇一個非中心點Or,用它代替某個現有的中心點Oj,計算這個代換的總代價S
4 .如果S<0,則用Or代替Oj,形成新的k箇中心點集合
5 重複2,直至中心點集合不發生變化
K中心法的實現:PAM-使用離差平方和來計算成本S
K中心法的優缺點:
1. 對於“噪音較大和存在離群值的情況,K中心法更加健壯,不像 Kmeans那樣容易受到極端資料影響
2.執行代價更高
3.基於密度的方法: DBSCAN(DBSCAN = Density-Based Spatial Clustering of Applications with Noise)
本演算法將具有足夠高密度的區域劃分為簇,並可以發現任何形狀的聚類
演算法基本思想
1 指定合適的 r 和 M
2 計算所有的樣本點,如果點p的r鄰域裡有超過M個點,則建立一個以p為核心點的新簇
3 反覆尋找這些核心點直接密度可達(之後可能是密度可達)的點,將其加入到相應的簇 ,對於核心點發生“密度相連”狀況的簇,給予合併
4 當沒有新的點可以被新增到任何簇時,演算法結束
注:(r-鄰域:給定點半徑r內的區域
核心點:如果一個點的r-鄰域至少包含最少數目M個點,則稱該點為核心點
直接密度可達:如果點p在核心點q的r-鄰域內,則稱p是從q出發可以直接密度可達 如果存在點鏈p1 ,p2 , …, pn,p1=q,pn=p,
pi+1是從pi關於r和M直接密度可達,則稱點p 是從q關於r和M密度可達的
如果樣本集D中存在點o,使得點p、q是從o關於 r和M密度可達的,那麼點p、q是關於r 和M密度相連的)
4.主成分分析法
原理及內容:
通過析取主成分顯出最大的個別差異,也用來削減迴歸分析和聚類分析中變數的數目
可以使用樣本協方差矩陣或相關係數矩陣作為出發點進行分析
成分的保留:Kaiser主張(1960)將特徵值小於1的成分放棄,只保留特徵值大於1的 成分
如果能用不超過3-5個成分就能解釋變異的80%,就算是成功***
通過對原始變數進行線性組合,得到優化的指標
把原先多個指標的計算降維為少量幾個經過優化指標的計算(佔去絕大部分份額)
基本思想:設法將原先眾多具有一定相關性的指標,重新組合為一組新的互相獨立的 綜合指標,並代替原先的指標
主成分分析的直觀幾何意義:
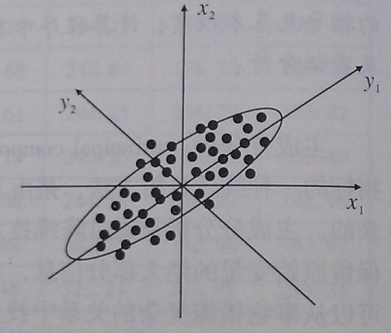
三、常用分類演算法
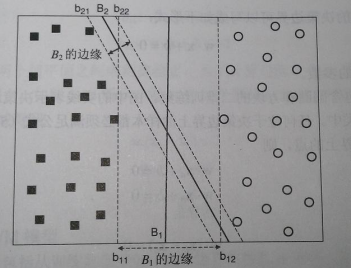
1.線性判別法
原理:用一條直線來劃分學習集(這條直線不一定存在嗎?),然後根據待測點在直線的哪一邊決定它的分類

2.距離判別法(關鍵度量指標:距離)
原理:計算待測點與各類的距離,取最短者為其所屬分類
常用距離:
1.絕對值距離
2. 歐氏距離
3.閔可夫斯基距離
4.切比雪夫距離
5.馬氏距離
6.Lance和Williams距離
7.離散變數的距離計算
各種類與類之間距離計算的方法:
1.最短距離法
2.最長距離法
3.中間距離法
4.類平均法
5.重心法
6.離差平方和法
3.貝葉斯分類法
原理:
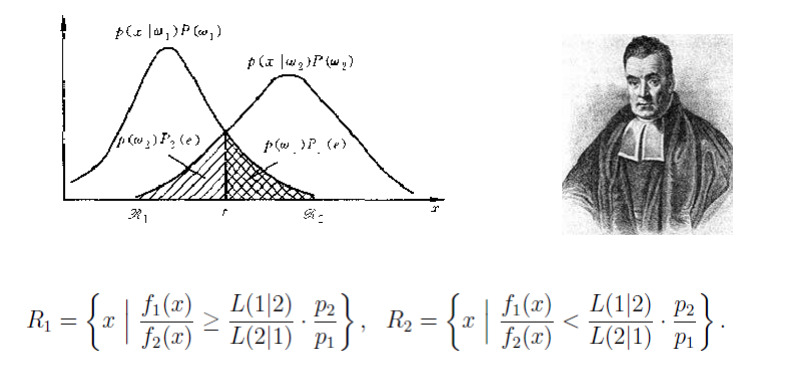
4.決策樹 decision tree
原理:輸入:學習集→分類模型(分類器)→分類規則(決策樹)
5. Knn演算法(k近鄰演算法)
演算法主要思想:
1.選取k個和待分類點距離最近的樣本點
2.看1中的樣本點的分類情況,投票決定待分類點所屬的類
6. 人工神經網路(ANN=Artificial Neural Networks)

影響精度的因素:
1.訓練樣本數量
2.隱含層數與每層節點數。層數和節點太少,不能建立複雜的對映關係,預測誤差較大 。但層數和節點數過多,學習時間增加,還會產生“過度擬合”的可能。預測誤差隨 節點數呈現先減少後增加的趨勢。
3.啟用函式的影響
神經網路方法的優缺點:
1.可以用統一的模式去處理高度複雜問題
2.便於元器件化,形成物理機器
3.中間過程無法從業務角度進行解釋
4.容易出現過度擬合問題
7.支援向量機 SVM
支援向量機,英文為Support Vector Machine,簡稱SV機。它是一種監督式學習的方法,它廣泛的應用於統計分類以及迴歸分析中。支援向量機將向量對映到一個更高維的空間裡,在這個空間裡建立有一個最大間隔超平面。在分開資料的超平面的兩邊建有兩個互相平行的超平面,分隔超平面使兩個平行超平面的距離最大化。
優化目標:決策邊界邊緣距離最遠